折现没错,但也请照顾未来的自己- 关于双曲折现(Hyperbolic discounting)
最近偶遇了一个概念:双曲折现(Hyperbolic discounting)
它是认知偏差的一种,概括来说就是, 我们看重当下利益、低估长远利益。得到利益前的延迟时间越长,对利益的价值评估便打越多折扣,两者关系近似于双曲线。
「当下利益优先」的现象大家都懂:坚持晨跑的对身心健康的益处抵不过赖床半小时的舒适,死线在下周的话不如先看一集剧再工作。但拖延真的可以简单地用「看重当下利益」来解释吗?经济学中的另一种折现方式是指数折现(exponential discounting)。这些数学模型一开始看得我一头雾水,于是今天仔细研究了下,觉得很有意思!

其实「折现」本身,并不是认知偏差。正常情况下,本来就是当下利益优先,任何未来的收益都要做出折现。三年后的100块可能只抵得上现在的80块。
传统经济理论是利用指数性的折现。例如第五期的利润为x, 折现成第一期的利润值就相当于𝛿^4x,其中𝛿<1就是两期之间的折现率。指数折现有一个非常重要的性质:决策者在期初所建立的最适跨期决策,有其时间上的一致性。决策者做过相应的成本效益分析后,会优先执行净收益更高的活动,放弃净收益为负的活动。这个分析今天做和一段时间后做,得出的结果是一样的。
然而心理学的许多实验都发现人类(动物也是) 对较近未来的折现率,远高于对遥远未来的折现率。
例如,美国心理学家Ainslie做了这样的实验:
- 实验的第一阶段,人们可以选择立刻得到$50,还是在六个月后得到$100;第二个阶段,他们可以选择在三个月后得到$50,还是九个月后得到$100。
- 绝大多数人在第一阶段选择立即拿到$50,而在第二阶段决定多等半年而得到翻倍的收益。
问题在于,两个选择本质上是相同的。同样的选择放在三个月后,人们出现了完全相反的行为!
双曲折现的重要特点是即时倾向性:在足够遥远的未来,决策者能够对比回报与付出,做出明智的选择,但在短期,我们更乐于逃避付出,及时行乐。
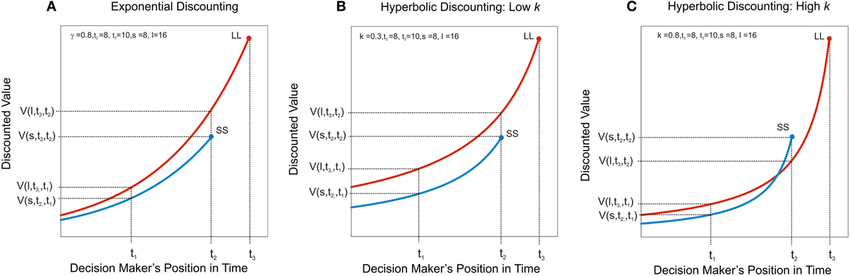
觉得上面的图很有帮助——横轴对应时间,纵轴对应收益——我用它举个栗子:
- 假设红线是去跑步,一小时后身体放松精神抖擞的收益曲线(长远的较高收益),蓝线是吃一盒冰激凌,半小时后糖分补足心情愉悦的收益曲线(短期的较低收益)。
- 图A用指数折现,看到不论在什么时刻选择,运动的收益都是大于甜食的收益。结论:快去运动啦~
- 折现率k决定了双曲线有多弯。图B中在k还很小的时候,长远的较高收益还是优于短期的较低收益。
- 图C则是高k值的双曲折现。随着时间的推近,到了t2… 啊啊啊怎么突然就甜食优先了xD? !
类似的例子有很多,对于好比戒烟、储蓄、准备考试这样会蛮辛苦的跨时决策,订立长期目标的时候该怎么选看得很清楚,但选择近在眼前时,即刻满足的选项突然变得无比诱人。
所以说,「当下利益优先」并不足以解释拖延之类的选择。双曲折现的模型更能反映人们的行为:我们的决策不具有时间一致性。
换句话说,「此刻的自己」会做出和「未来的自己」不同的选择。
在我们的幻想中,未来的自己更理智,更勤奋,更聪明。尴尬的是未来的自己并没有变得那么厉害。
这个模型在广告和营销中应用很多,在公共政策上的应用也很有趣(例如从工资中扣除养老金,公共场所禁烟)。在《简介行为经济学》里读到:「Laibson(1997)曾经利用一个可以用来近似(approximate)双曲折现,但又同时拥有指数折现良好之数学性质的半双曲(quasi-hyperbolic) 折现模型, 成功的计算出人的跨时储蓄选择行为。」
不明觉厉QAQ我得补课数学。
好麻烦呐><
未来的我会好好学习的吧。
参考:
陈恭平人非圣贤:简介行为经济学http://idv.sinica.edu.tw/kongpin/teaching/micro/behavioral economics.pdf
Martuscello, J. (2017, December 17). New Perspectives into How Consumers Choose. (Behavioral Economics & HYPObolic Discounting). Retrieved from https://medium.com/@jasonmartuscello/new-perspectives-into-how-consumers-choose-behavioral-economics-hypobolic-discounting-ed399ec359b5
Story, Giles & Vlaev, Ivo & Seymour, Ben & Darzi, Ara & Dolan, Raymond. (2014). Does temporal discounting explain unhealthy behavior? A systematic review and reinforcement learning perspective. Frontiers in behavioral neuroscience. 8. 76. 10.3389/fnbeh.2014.00076.
喜欢我的作品吗?别忘了给予支持与赞赏,让我知道在创作的路上有你陪伴,一起延续这份热忱!
