随机森林（上）

2020 年 11 月 17 日

暑假里说要写一篇文章来写随机森林，当时的动机是想要通过输出一些知识来帮助自己归纳整理，当然也有一点小孩子学到了新东西想要炫耀的意味。因为考虑到自己的知识结构还是比较零散的，所以如果单独拎出一个概念，有点唐突。但是不妨这样做，给自己的学习经历打下一个标记。

· Part1 ｜树

说到森林，必然联想到树。所以，我们先可以撇开随机森林的随机，把重点放在树上。

这里的树，指的是决策树(Decision Tree)，也就是我们平时看到的树状结构，我们可以对样本依据决策树进行分类。比如我们这里用一个简单的模型说明一下，样本中一共有12个人。最终的结果是要划分“是否为NBA受众”。

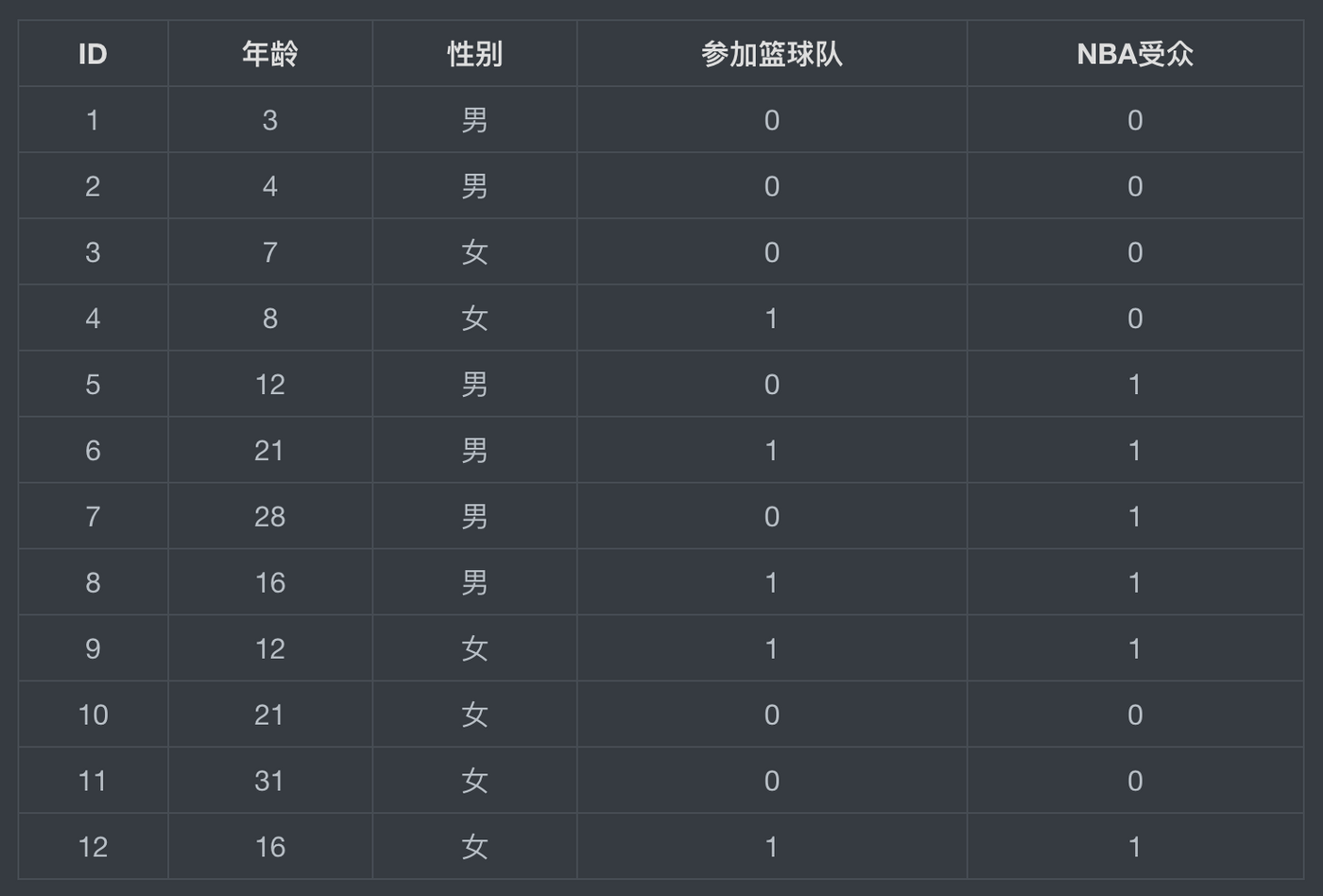
首先概括来说：一棵决策树是一个树结构（可以是二叉树或非二叉树），每个非叶节点对应一个特征，该节点的每个分支代表这个特征的一个取值，而每个叶节点存放一个类别或一个回归函数。

其次来解释下决策树的一些关键的术语：在案例中，我们首先看到最上面的“年龄>10”这一特征作为这棵树的出发点，即根节点(root node)。而之后的条件“是否男生”，“参加篮球队”都被称作非叶结点(none-leaf node)，分支的最后的结果是叶子结点(leaf node)。Y或N可以视作对该特征的取值成了分支(branches)。当然有的情况下，比如天气状况作为特征（多云，晴，下雨）可以多分枝，组成非二叉树。

· Part2｜熵

为什么要寻找这些特征？我们为什么要进行分叉？

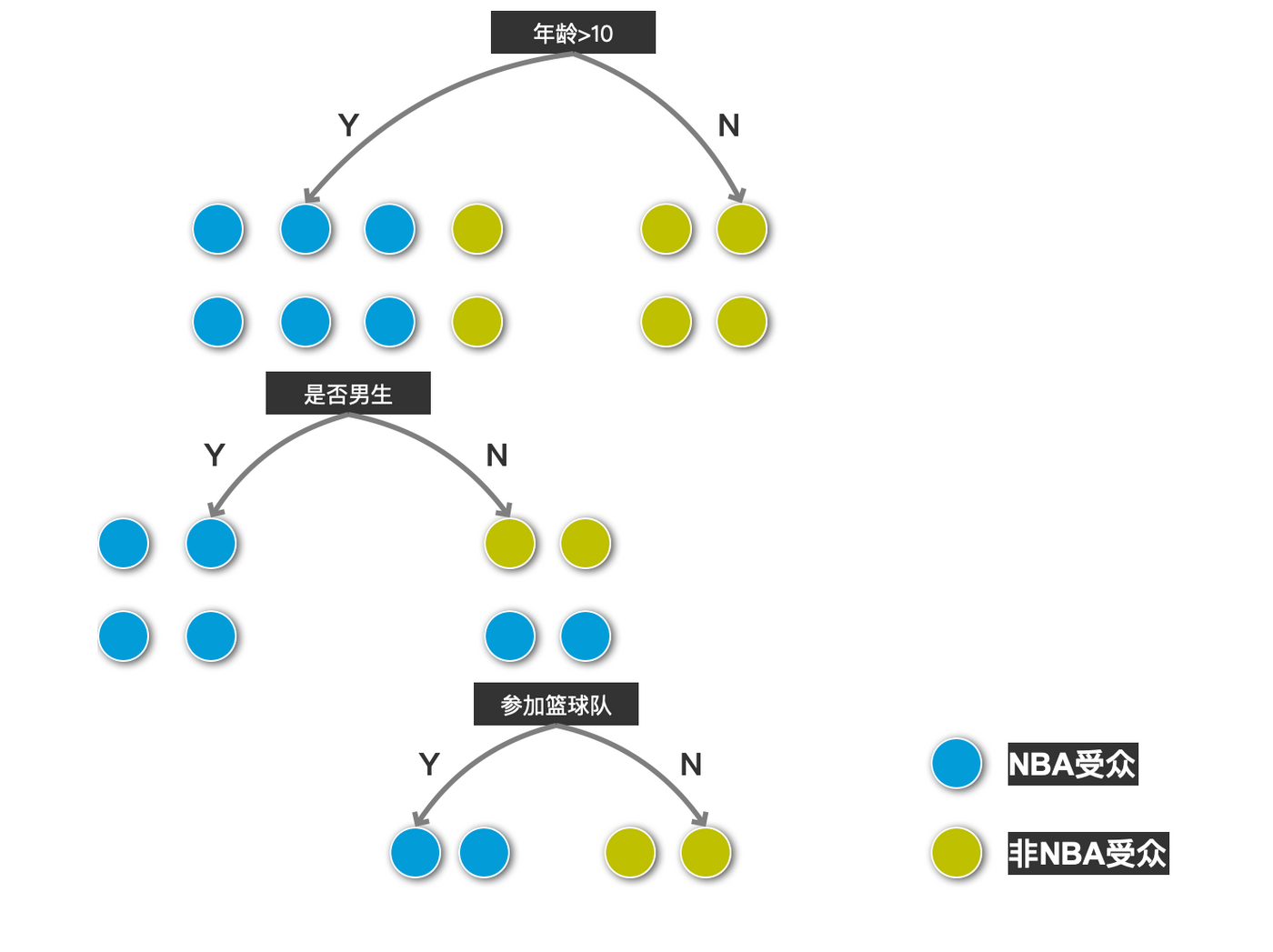
不妨更加简化，把X和Y看作两个特征，先可以对特征Y进行分类是满足Y>3，其次再划分X的区间。划分的目的是区分两种颜色，也就是使得每一次划分的子集纯度更高。这里就需要引入熵(Entropy)的概念。

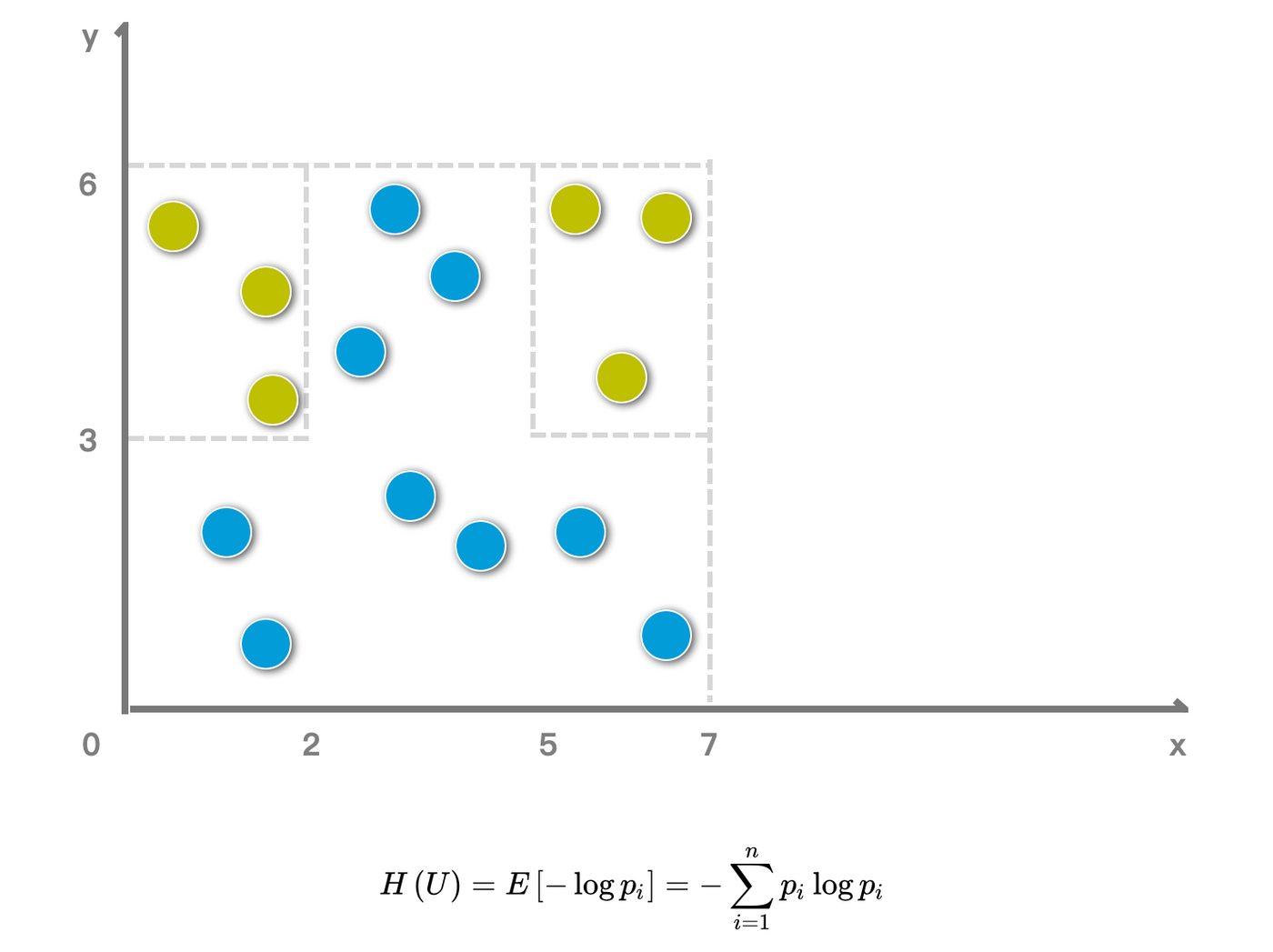
根据公式可以计算本身样本不做分类时的熵：-6/15*ln(6/15)-9/15*ln(9/15) = 0.67，一般也用log2，这里为了按计算器方便。

如果这时，我们通过对特征Y进行分类，则可以分为上下两部分：Y>3部分的熵为-3/9ln(3/9)-6/9ln(6/9) = 0.64，Y<3的部分则肉眼可见充满purity，所以熵为0。通过特征Y的分类，我们可以计算分类之后的熵，也就是给每个分支的熵乘上权重，9/15*0.64=0.38。

信息增益=熵0-熵1=0.26

同样，作为比较，如果我们先用特征X来分，可以分成三部分(X<2,2<X<5,X>5)，结果是5/15（-3/5ln(3/5)+-2/5ln(2/5))+0+5/15（-3/5ln(3/5)+-2/5ln(2/5))=0.448。

信息增益=熵0-熵2=0.22

但是有人就会问，我们再回到第一个案例，给每个人标上ID。根据ID来直接分出12个不同的人，那么在计算熵不就为0了吗？

的确，上面的算法是ID3(Iterative Dichotomiser 3)，因为取值种类多的特征会有相对较大的信息增益——信息增益反映的是给定一个条件以后不确定性被减少的程度，必然是分得越细的数据集确定性更高（上面坐标的例子不够极端，但是标号的情况可以很好体现）。被取值多的特征分裂，分裂成的结果也就容易细；分裂结果越细，则信息增益越大。

因此就有了后来的C4.5，选用信息增益率(Gain Ratio)用比例而不是单纯的量作为选择分支的标准。简单的说就是要惩罚拥有很多属性的特征且每个属性的样本数量占比很少的情况。熵0=2-1/2ln1/2=0.69

所以Gain Ratio = 信息增益/该特征下的熵，也就是-121/12ln(/12)=2.48，由此得到信息增益率=信息增益/特征熵28%。而我们通过例子中对年龄进行分类后可计算熵=0.37，增益为0.32，该特征下自身的熵=0.63，增益率为50%。

最后一种是CART( Classification and Regression Tree) 算法。CART 算法的运行过程和 ID3 及 C4.5 大致相同，不同之处在于：

CART 的特征选取依据不是增益量或者增益率，而是 Gini 不纯度（Gini impurity），每次选择 Gini 系数最小的特征作为最优切分点。
CART 是一棵严格二叉树。每次分裂只做二分（这就是后面Gini impurity计算方式和二项分布的方差一样的原因？）

CART选取特征的标准是根据Gini impurity：

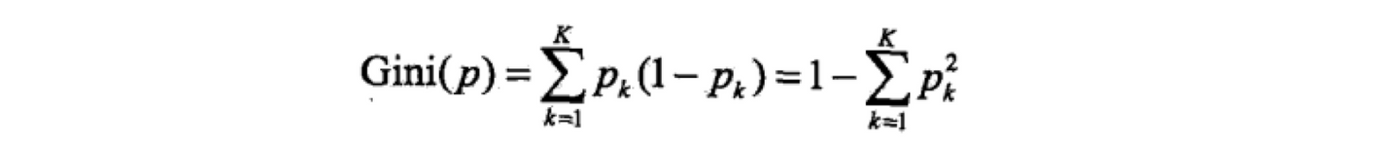
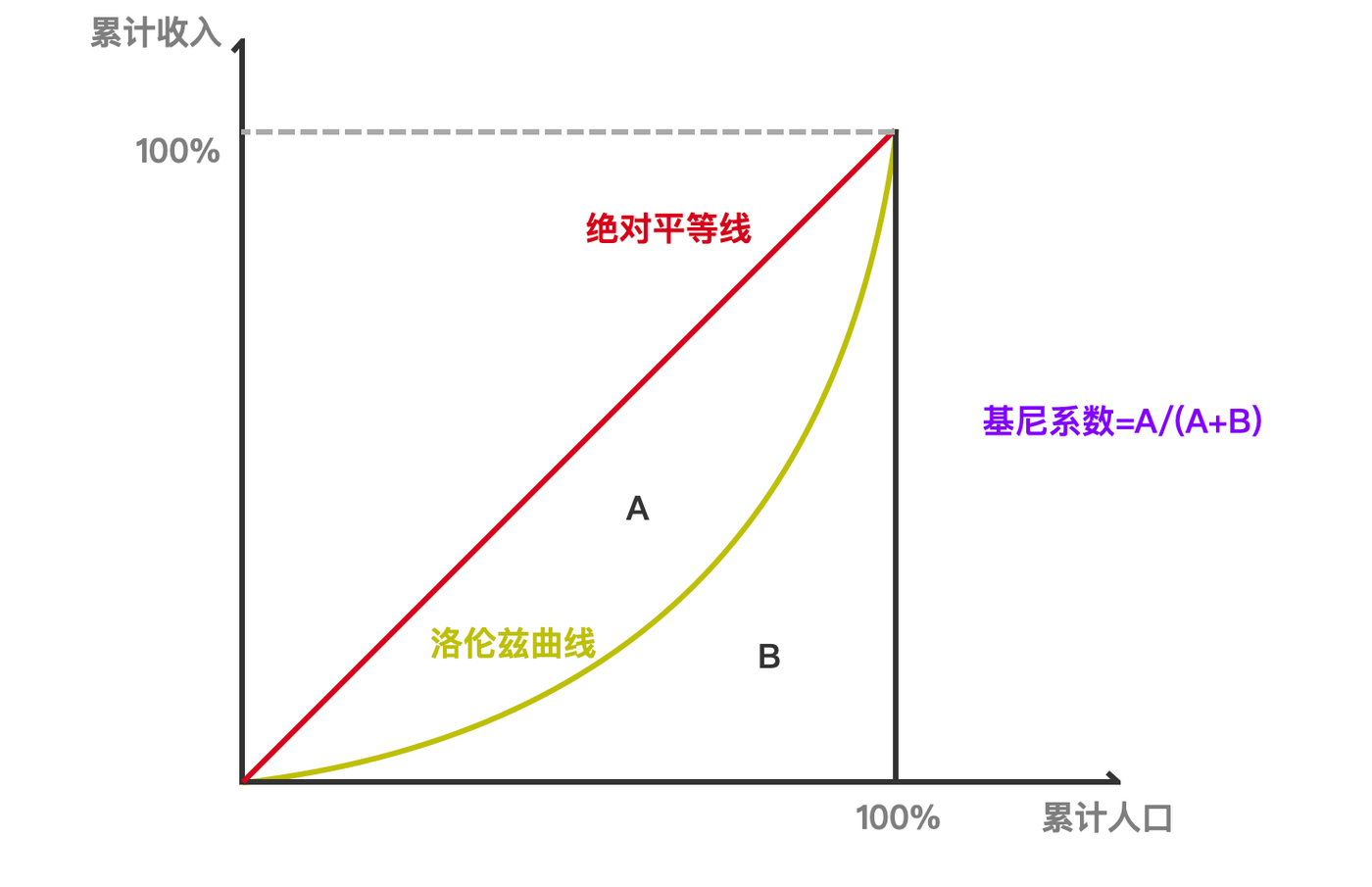
感觉另一个基尼系数(Gini Coefficient)是不是很耳熟，就是用来反映收入差距的指数，似乎二专经济学里的劳伦兹曲线(Lorenz Curve)也是描述这点。基尼系数最大为“1”，最小等于“0”。基尼系数越接近0表明收入分配越是趋向平等。Gini coefficnet针对于二元分类问题。对于二元分类问题，我们的预测结果会有对应的ROC AUC，那么Gini Coefficient=2AUC−1。

有的地方会用Gini Index，这是不太正确的说法，要根据具体的情况判断，防止误用。