Machine Learning - 資料預處理- 特徵工程- 標準化(Standard Scaler) 公式教學與Python程式碼實作教學

2020 年 10 月 22 日

yoyo~~最近在進行資料視覺化開發時，遇到一個小問題，就是每個指標的值範圍大小不一，有的非常大，有的則非常小，這樣繪出來的圖很難直覺地看出趨勢，指標範圍大的會讓指標範圍小的在圖中變得很像一條平行線，於是我就想到了標準化的方法，它能幫助我把所有指標縮放到同一個範圍內，這樣就能一眼看出每個指標的趨勢，這邊我也想將我在網路上所學習的標準化方法分享給大家，也針對各種公式進行Python程式碼的實作，這樣大家就能用我的程式碼，快速地實現標準化的過程喔，讓我們開始吧

標準化是什麼?

簡單來說，就是將特徵值縮放成一個特定區間內的值，像是我把班上所有同學的身高與體重的值用0~1區間的值替代，也就是縮放到0~1區間的意思喔

為什麼要標準化?

通常我們的數據包含了許許多多的特徵資料，而這些特徵所代表的數值意義卻是截然不同的，像是體重的25(公斤)，跟身高的180(公分)，如果單以數值來講180大於25，但是它們的特徵意義不同，可以這樣比較嗎?所以我們必須將這些特徵值縮放到一個特定區間內，才能進行比較

標準化對資料分析有什麼好處?

可以幫助優化梯度下降法:

當資料未進行標準化時(如圖左邊)，以這張圖的數據為例，可以看出在X軸的特徵值，取值範圍較Y軸的特徵值小，進行梯度下降法找尋最佳解時(如圖中紅線)，會因為範圍拉的很長，導致需要迭代許多次才能找到，但是進行標準化後(如右圖)，梯度下降的迭代次數就明顯的減少許多次

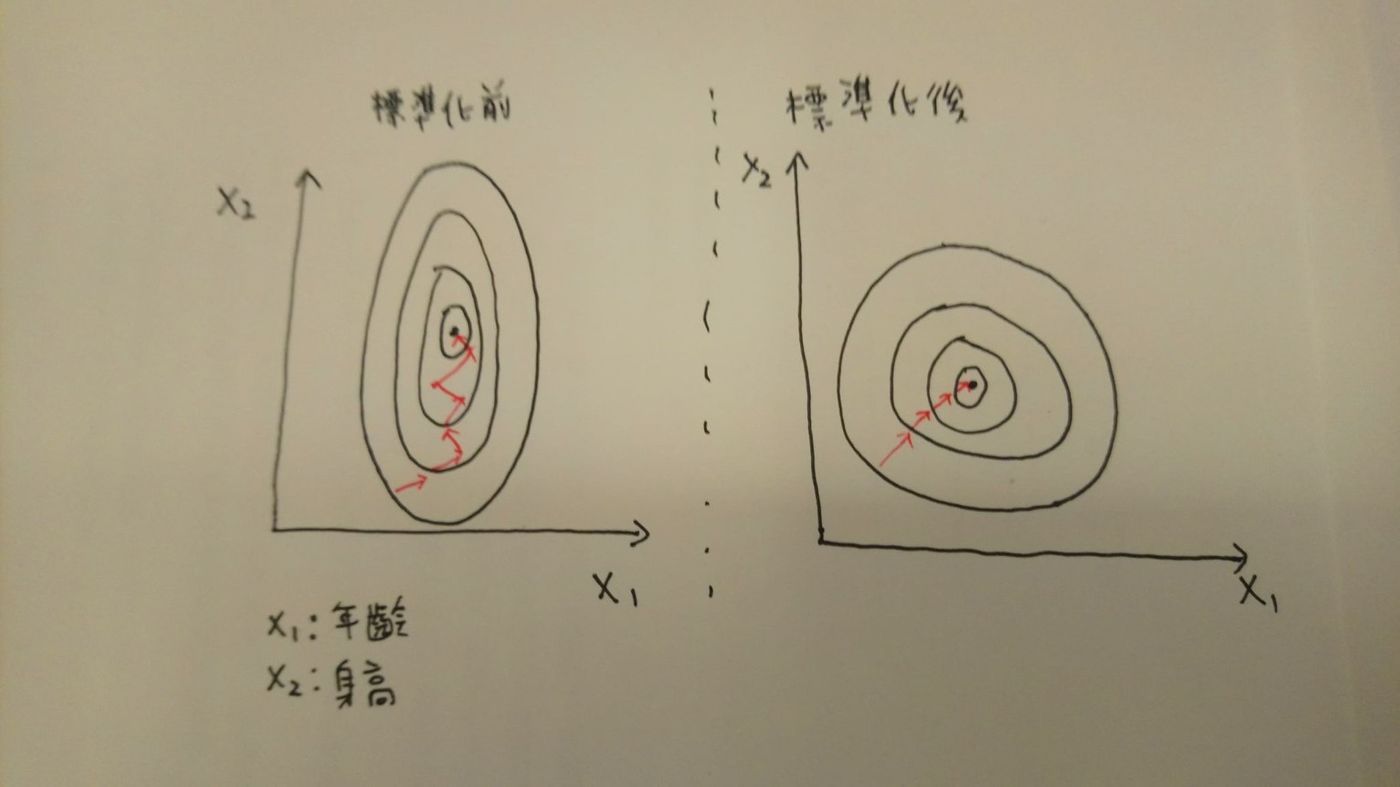
提高數據預測的精準度

以KNN算法為例，我們利用數據間特徵值的歐式距離來進行分類，如ˇ我今天有些特徵值範圍比較大，像是身高，有些則較小，像是體重，但是可能在這次的預測問題中體重這個特徵比較有影響，像是我想預測是吃貨的機率，那這時候就會因為沒有進行標準化(Standard Scaler)，造成身高的影響可能較高，導致最後的模型預測不準，所以進行標準化後，可以很容意地知道，預測準確率會有所提升

標準化方法有哪些？

Z-Score: 將數據呈現正態分佈（或稱常態分佈）與中心化

說明：進行Z-Score標準化後，數據會呈正態分佈，並且會將數據縮放成平均為0，平方差為1的數據
公式：

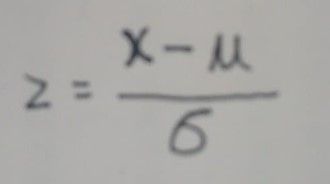
變數解釋：

z: 標準化後的數據 
x: 標準化前的數據（原始數據） 
μ: 均值 
σ: 全部數據的標準差

補充：標準差計算公式
母體標準差： 如下公式，根號裡面是變異數（variance）的計算公式，結果開根號即為標準差，數據X1,X2...XN，N為母體總數，μ為平均數

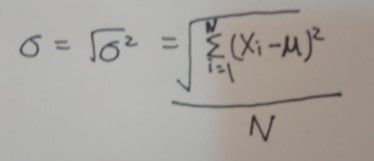
樣本標準差：如下公式，簡單來說就是數據總數N要減1 5. 程式碼範例：這邊我有兩組數據A與B，我要繪製一個未進行標準化與進行標準化（Z-Score）的圖形比較

程式碼範例: 這邊我有兩組數據A與B，我要繪製一個未進行標準化與進行標準化-Z-Score後的圖形比較

## 導入所需的套件
import plotly
import plotly.graph_objs as go
import math
import pandas as pd

## 建立數據集
data_a = [28,32,26,38,42,66,40,42,64,66,78,20,38,66,42,58,28,36,34,66]
data_b = [68,78,58,76,54,58,60,78,52,44,28,80,58,99,46,56,39,37,28,66]
time = [1,3,5,6,7,8,9,10,14,16,19,25,26,28,30,32,36,38,42,58]

## Z-Score標準化
def z_score_y(raw_data):
  print(raw_data)
  ## 計算數據平均數
  total = 0
  for d in raw_data:
    total += d
  aver = total/len(raw_data)
  
  ## 計算所有數據減掉平均數的平方相加
  data_s = 0
  for s in raw_data:
    data_s += (s - aver)**2
  
  ## 計算剛剛的結果除以數據總數開根號即為標準差
  std = math.sqrt(data_s/len(raw_data))
  
  ## 將每個數據減掉平均數除以標準差成為新的數據串列
  ## 裝新的標準化後的數據串列
  z_score_data = []
  for z in raw_data:
    z_score_data.append((z - aver)/std)
  
  ## 回傳結果
  return z_score_data
  
  
## 繪製數據
data1 = go.Scatter(x = time, y = data_a, mode = "lines+markers", name = '原始數據A', line_width = 2, 
         marker_size = 4)
data2 = go.Scatter(x = time, y = data_b, mode = "lines+markers", name = '原始數據B', line_width = 2, 
         marker_size = 4)
  
data3 = go.Scatter(x = time, y = z_score_y(data_a), mode = "lines+markers", name = 'A: Z-Score標準化', line_width = 2, 
         marker_size = 4)  

data4 = go.Scatter(x = time, y = z_score_y(data_b), mode = "lines+markers", name = 'B: Z-Score標準化', line_width = 2, 
         marker_size = 4)  



## 介面設定
layout = go.Layout(
  title = 'Z-Score',
  xaxis = {'title':'Time'},
  yaxis = {'title':'Value'},
  showlegend = True,
  autosize = False,
  width = 1000,
  height = 400,
  margin = dict(l = 2, r = 2, b = 0, t = 60),
  plot_bgcolor = "#B9B9ff",
  paper_bgcolor = '#ACD6FF',
  font = {
    'size': 28,
    'family': 'fantasy',
    'color': 'darkblue'
 },
  
)
  
  
## 組合成Figure
figure = go.Figure(data = [data1, data2, data3, data4], layout = layout)

## 顯示圖像
figure.show()

執行結果

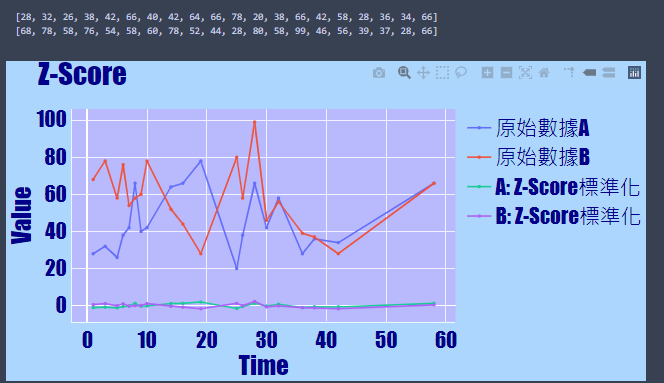
這張圖是互動的圖喔!! 大家可以自己試試它的互動效果，像是我想關注標準化後的圖就好(如下圖)，只要輕鬆在圖片上操作就可以囉，不用動到程式碼

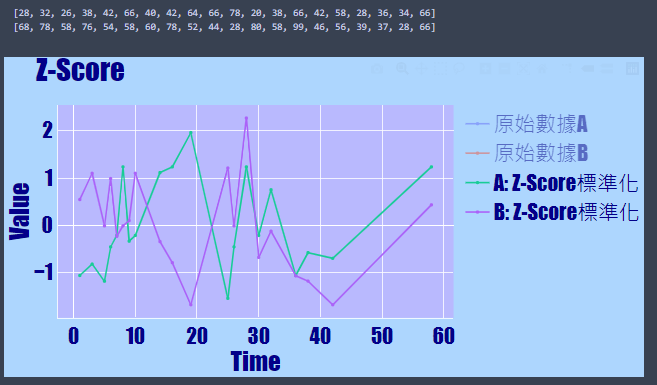
執行圖片結果：未進行標準化與進行標準化（Z-Score）的圖形比較，可以看出原始資料A與原始資料B，原本的線差距也許很大，但經過標準化（Z-Score）後，它們都被縮放到接近的位置
單獨看標準化（Z-Score）後的圖形，會發現它會呈現正態分佈
提醒：我這邊不會講解如何繪圖喔，有興趣的大家可以參考我接下來會寫的Plotly文章喔，那邊會詳細教大家如何繪圖

Min-Max線性歸一化

說明：進行Min-Max標準化後，因為計算公式的關係，當X為最大值時，標準差就為1，最小值轉化為0，所以我們的數據將會縮放到0～1之間喔，這樣的方式使我們的數據分佈型態不會有變化喔
公式：

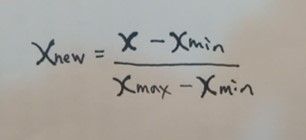
變數解釋

Xnew: 標準化後的數據
Xmax: 數據中的最大值 
Xmin: 數據中的最小值 X: 標準化前的數據

程式碼範例：這邊我有兩組數據A與B，我要繪製一個未進行標準化與進行標準化（Min-Max）的圖形比較

## 導入所需的套件
import plotly
import plotly.graph_objs as go
import math
import pandas as pd

## 建立數據集
data_a = [28,32,26,38,42,66,40,42,64,66,78,20,38,66,42,58,28,36,34,66]
data_b = [68,78,58,76,54,58,60,78,52,44,28,80,58,99,46,56,39,37,28,66]
time = [1,3,5,6,7,8,9,10,14,16,19,25,26,28,30,32,36,38,42,58]

## Min-Max 歸一化
def min_max_y(raw_data):
  
  ## 裝進標準化後的新串列
  min_max_data = []
  
  ## 進行Min-Max標準化
  for d in raw_data:
    min_max_data.append((d - min(raw_data)) / (max(raw_data) - min(raw_data)))
  
             
  ## 回傳結果
  return min_max_data

## 繪製數據
data1 = go.Scatter(x = time, y = data_a, mode = "lines+markers", name = '原始數據A', line_width = 2, 
         marker_size = 4)
data2 = go.Scatter(x = time, y = data_b, mode = "lines+markers", name = '原始數據B', line_width = 2, 
         marker_size = 4)
  
data3 = go.Scatter(x = time, y = min_max_y(data_a), mode = "lines+markers", name = 'A: Min-Max 歸一化', line_width = 2, 
         marker_size = 4)  

data4 = go.Scatter(x = time, y = min_max_y(data_b), mode = "lines+markers", name = 'B: in-Max 歸一化', line_width = 2, 
         marker_size = 4)   
  

## 介面設定
layout = go.Layout(
  title = 'Min-Max',
  xaxis = {'title':'Time'},
  yaxis = {'title':'Value'},
  showlegend = True,
  autosize = False,
  width = 800,
  height = 400,
  margin = dict(l = 2, r = 2, b = 0, t = 60),
  plot_bgcolor = "#B9B9ff",
  paper_bgcolor = '#ACD6FF',
  font = {
    'size': 26,
    'family': 'fantasy',
    'color': 'darkblue'
 },
  
)
  
  
## 組合成Figure
figure = go.Figure(data = [data1, data2, data3, data4], layout = layout)

## 顯示圖像
figure.show()

執行結果

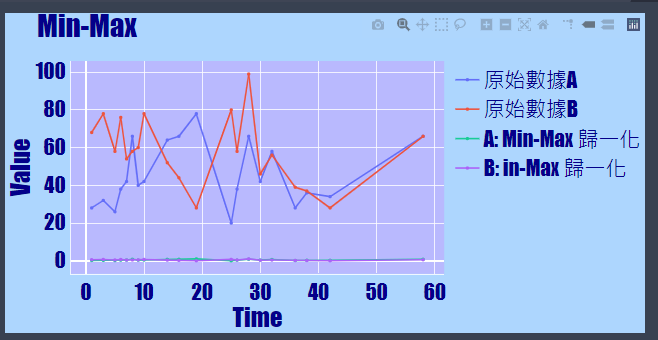
執行圖片結果：未進行標準化與進行標準化（Min-Max）的圖形比較，可以看出原始資料A與原始資料B，原本的線差距也許很大，但經過標準化後，它們都被縮放到接近的位置
單獨來看標準化（Min-Max）後的圖形，會發現它會將數據縮放到介於0～1之間

MaxAbs: 最大絕對值標準化方法

說明：當數據中有負數時，使用MaxAbs標準化方法就能保有數據的正負屬性，我們需要將數據都取絕對值後，找尋最大值當分母，然後每個數據值分別除以它來進行標準化，它會將數據縮放到介於-1～1之間
公式:

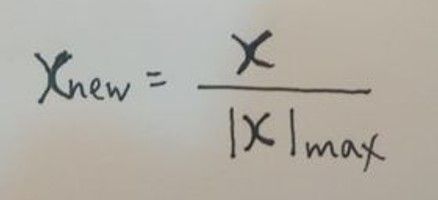
變數解釋：

Xnew: 標準化後的數據 
X： 標準化前的數據 
|X|max: 數據取絕對值後的最大值

程式碼範例：這邊我有兩組數據A與B，我要繪製一張未進行標準化與進行標準化（MaxAbs）的圖形比較，這次我會在原始資料中加入負數的數據值

## 導入所需的套件
import plotly
import plotly.graph_objs as go
import math
import pandas as pd

## 建立數據集
data_a = [28,-32,26,38,42,66,40,42,64,-66,78,20,-38,66,42,58,28,36,34,66]
data_b = [68,-78,58,76,54,58,60,78,52,44,28,80,-58,-99,46,56,39,37,-28,66]
time = [1,3,5,6,7,8,9,10,14,16,19,25,26,28,30,32,36,38,42,58]


## Maxabs 標準化
def maxabs_y(raw_data):
  
  ## 裝進標準化後的新串列
  maxabs_data = []

  ## 將數據全部先取絕對值，裝進一個站存串列中，為了找尋絕對值後的最大值
  temp_data = []
  for i in raw_data:
    temp_data.append(abs(i))
  
  ## 進行Maxabs標準化
  for d in raw_data:
    maxabs_data.append(d / max(temp_data))

  ## 回傳結果
  return maxabs_data
             
             
             
## 繪製數據
data1 = go.Scatter(x = time, y = data_a, mode = "lines+markers", name = '原始數據A', line_width = 2, 
         marker_size = 4)
data2 = go.Scatter(x = time, y = data_b, mode = "lines+markers", name = '原始數據B', line_width = 2, 
         marker_size = 4)
  
data3 = go.Scatter(x = time, y = maxabs_y(data_a), mode = "lines+markers", name = 'A: Maxabs 標準化', line_width = 2, 
         marker_size = 4)  

data4 = go.Scatter(x = time, y = maxabs_y(data_b), mode = "lines+markers", name = 'B: Maxabs 標準化', line_width = 2, 
         marker_size = 4)   
  

## 介面設定
layout = go.Layout(
  title = 'Min-Max',
  xaxis = {'title':'Time'},
  yaxis = {'title':'Value'},
  showlegend = True,
  autosize = False,
  width = 800,
  height = 400,
  margin = dict(l = 2, r = 2, b = 0, t = 60),
  plot_bgcolor = "#B9B9ff",
  paper_bgcolor = '#ACD6FF',
  font = {
    'size': 26,
    'family': 'fantasy',
    'color': 'darkblue'
 },
  
)
  
  
## 組合成Figure
figure = go.Figure(data = [data1, data2, data3, data4], layout = layout)

## 顯示圖像
figure.show()

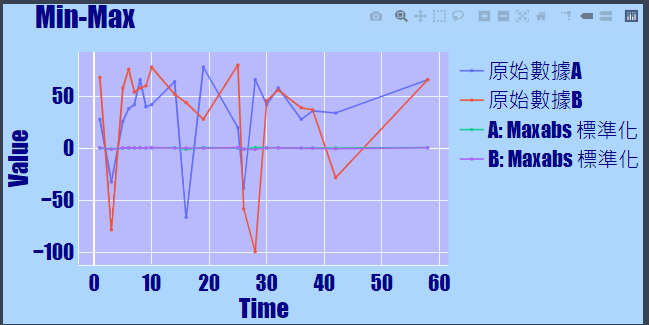
執行結果

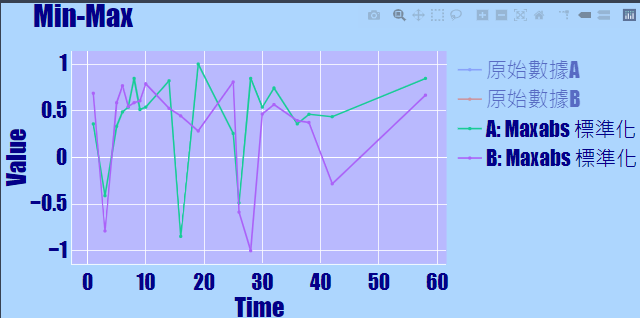
將原始數據先點掉，focus在Min-Max後的結果

執行圖片結果: 未進行標準化與進行標準化(MaxAbs)的圖形比較結果，可以看出原始資料A與原始資料B，原始資料的線差距也許很大，但經過標準化後，它們都被縮放到接近的位置(介於-1~1之間)(如第二章圖)
單獨來看標準化(MaxAbs)後的圖形，會發現它會將數據縮放到介於-1~1之間

RobustScaler

當數據中出現異常值(離群點)，如果使用Z-Score會導致數據失去這樣的特性，此時就是最好使用RobustScaler的時機點，它對於數據中心化與縮放的統計資料是基於百分位數，所以不受少量的離群點影響，它也擁有較強的參數調節能力，能針對數據中心化與縮放進行更強的調節
計算方法: RobustScaler根據分位數範圍，刪除中位數，然後進行資料的縮放，分位數範圍預設為IQR(Interquartile Range)，它代表第1四分位數(前25%的分位數)與第3四分位數(前75%的分位數)之間的範圍距離
由於它的計算方法比較複雜，所以我會在接下來針對使用sklearn來進行標準化的一篇，帶大家直接使用sklearn進行實作喔，這邊就不進行實作囉

這一篇主要帶大家了解標準化的意義與如何使用城市進行手動計算，下一篇針對使用sklearn來進行標準化的一篇，我會與大家一起學習如何使用機器學習套件快速隊資料進行標準化喔!! 希望這一篇有幫助到您~~ 如果有哪裡寫錯或有什麼地方想與我討論的，都很歡迎喔~~

當然標準化的方法還有許多種不同的計算方式，我這邊就不一一介紹囉，有興趣的大家可以自行查找，或參考這篇(https://kknews.cc/zh-tw/code/3a549r8.html)裡面的表格圖片(https://i2.kknews.cc/SIG=2gqol87/ctp-vzntr/po02nrrq9o6s41n883ps7qq50np838p3.jpg)喔

Reference

https://www.itread01.com/content/1500483372.html

https://www.itread01.com/content/1544753542.html

https://kknews.cc/zh-tw/code/3a549r8.html

https://www.itread01.com/content/1525191604.html

CC BY-NC-ND 2.0 授权

喜欢我的作品吗？别忘了给予支持与赞赏，让我知道在创作的路上有你陪伴，一起延续这份热忱！

為自己CodingYO~~ 剛跨入AI人工智慧領域的小小工程師, 熱愛自學, 熱愛分享, 下班後的我想為自己Coding, 積極撰寫教學文, 想將自學的程式知識分享給大家, 不斷追求進步的自己, 希望有一天能回饋社會，幫助需要幫助的人, 如果您有什麼很酷的想法，也覺得我還行，歡迎您找我合作~~ IG: https://www.instagram.com/coding_4_me/

来自作者
相关推荐

Machine Learning - 資料預處理- 特徵工程- 標準化(Standard Scaler) 公式教學與Python程式碼實作教學

標準化是什麼?

為什麼要標準化?

標準化對資料分析有什麼好處?

標準化方法有哪些？

Z-Score: 將數據呈現正態分佈（或稱常態分佈）與中心化

MaxAbs: 最大絕對值標準化方法

Reference

[Takeaways]原力效應 — Part1

[行銷5.0] 人工智慧的緣起

[Aptos學習筆記#8]Move進階使用 - Resource介紹一

[Takeaways]原力效應 — Part1

[行銷5.0] 人工智慧的緣起

[Aptos學習筆記#8]Move進階使用 - Resource介紹一