Risk Parity 和全天候基金

為什麼大家會注意「資產配置」? 我猜很多人和我一樣,想花時間充實生活和提升自己,因此採用宏觀的投資角度,希望資產隨時間成長。投資者計畫、投入、等待、收穫,優雅而愜意。
本質上,我們把資金丟到市場上承擔風險,以獲得長期的報酬。因此,當人們在說資產配置時,意思是拿捏各類資產的比例,以調配出理想的風險和回報。不過,我覺得「預期風險」本身是件好笑的事,如果我都能準確掌握了,它還能叫風險嗎? 真正傷人的,不是學界或業界定義的「波動」,而是預料之外的虧損。所以,如果該發生的都會發生,那麼製造危險的不是金融工具,而是人類自己的思想缺陷,Dalio也這麼覺得。
1. 1971森林體系瓦解的時候,Ray Dalio正看著電視。他心想,既然紙幣和黃金脫鉤了,也就失去原本的價值。隔天早上Dalio走進紐交所,滿心期待股市暴跌,但當天的道瓊指數卻大漲4%,而黃金衝得更高。從此他受到很大的啟發,也開始意識到,投資人無法準確理解經濟事件對投資組合的影響,而且經驗往往無法帶來正確答案,哪怕是職業玩家。更重要的,Dalio也在試圖建構一種策略,能夠適應所有的經濟環境,而不需依賴投資者的主觀判斷。
換句話說,Dalio希望策略穩定獲利,而且讓投資者能安心睡覺。全天候基金的精神,就是針對不同經濟背景擬定策略,然後將「風險」平均配置到這些情境中。因此,與其說Dalio在配置資產,不如說他配置風險到不同資產。
我從Dalio的橋水基金公司擷取這個風險象限,讀者也可以看英文原版。

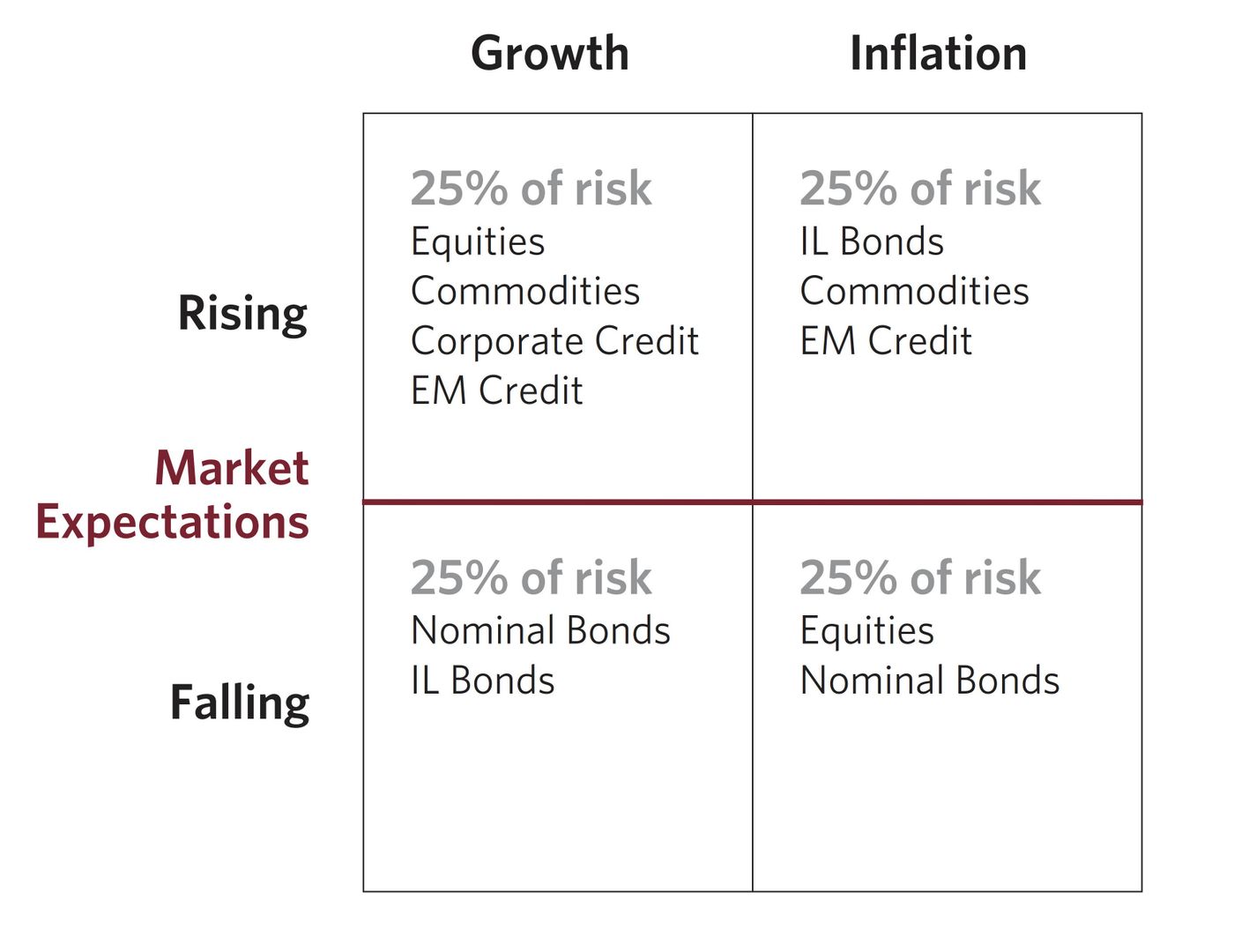
我們可以把市場環境用「經濟升降」和「通膨增減」來劃分,這個概念和「美林時鐘」有異曲同工之妙,只不過切割方法不同。因此,象限之下就有通膨、通縮、經濟成長和經濟萎縮等四個狀況,而Dalio也把相應資產放進這個框架。
定性來看,全天候的概念很好複製。除了橋水外,黑石、AQR和PanAgora(磐安)也有全天候基金,而各位同樣可以配置自己的全天候策略。不過,觀眾看到這裡,應該知道我喜歡定量解釋策略背後的原理,所以何不拿起計算機繼續看下去?
2. 既然要把風險平均配置,我們就應該清楚如何實踐,而不是憑感覺。
通常股票的波動性比債券還大,因此傳統股債6/4配置,會把大部分風險集中在股票上,這是某些投資人不樂見的。另外,雖然Dalio的全天候基金,將風險平均分散,但「風險均衡」(risk parity)這個名詞,直到2005年才被提出。
錢恩平博士(Edward Qian, CFA),在磐安資管工作時發表了一篇Risk Parity Portfolios,從此大家都沿用這種說法。Qian也寫了一本Risk Parity Fundamentals,詳細描述了風險均衡(風險平價)理論發展的歷史,也有中譯版,如果你覺得我說得不清楚,也可以去找原書來看。(錢的另一本Quantitative Equity Portfolio Management也是我推薦的書,讀者有興趣不妨試閱。)
想要體會風險的「不均衡」,我們直接拿傳統股債結合開刀吧。
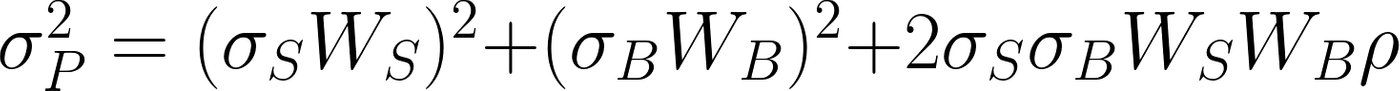
ρ: 相關係數
假設股票波動率是2.5%,債券0.5%,相關係數是0.3,那麼6/4組合波動是 (0.6×2.5)²+(0.4×0.5)²+2×2.5×0.5×0.6×0.4×0.3=2.4316%. 其中關於協方差部分,股債「各占一半」,因此股票貢獻的波動率是 (0.6×2.5)²+1×2.5×0.5×0.6×0.4×0.3=2.34%,債券部分是(0.4×0.5)²+1×2.5×0.5×0.6×0.4×0.3=0.13%。換句話說,股票和債券對於波動率的占比是94.7%和5.3%,差距懸殊。
如果按照風險均衡的思路,我們應該多配一點低波動資產(例如債券),這樣才能讓各類資產的風險貢獻相當,或至少在我們的預期範圍內。
3. 簡單說,風險平價策略,有兩個特點。
第一,直接放棄預期收益,只從風險出發。第二,較少最優化步驟,因此計算容易一些。我們回頭看看幾十年前Markowitz的MVO,同時考量風險和報酬,並在約束條件下最優化。後來有Black Litterman等人,試著透過合理化預期報酬,來修正MVO對參數敏感的缺點。而隨著理論演進,Risk Parity選擇對預期收益投降,它只注重風險本身。
也就是說,在風險均衡的世界,投資者應該將風險多元分散,而不是只考慮資產的特性,這才是「把雞蛋放在不同的籃子裡」。另外,透過組合波動的算式,我們可以看出,由於風險貢獻包含了相關係數,因此當兩個資產高度相關時,它們會被模型當作類似的風險來源,我們也可以受益於這類「解釋性」。
有些投資者會發現,風險均衡策略傾向於配置多一點低波動資產,但低波動通常也意味著低收益,所以組合收益往往會比傳統配置還低。那怎麼辦? 上槓桿啊。
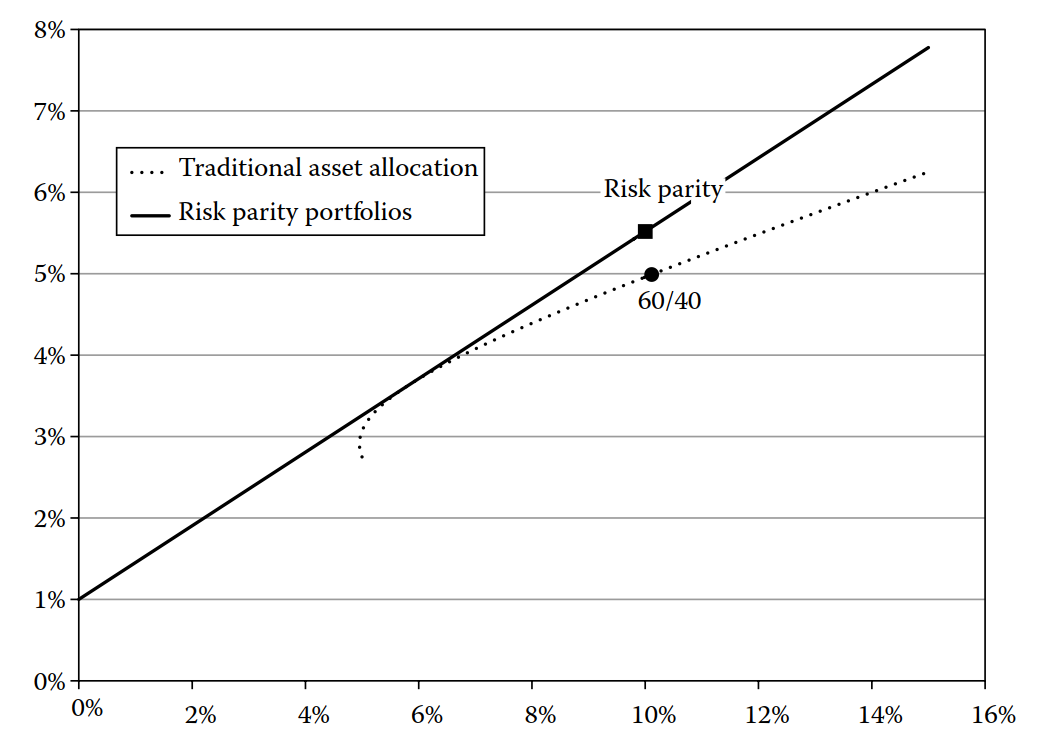
圖中的雙曲線,我應該不用說明了。在傳統MVO的組合下,我們如果要更高收益,就需要往高波動資產靠攏,但也需要承受邊際效用遞減,並不划算。至於Risk Parity那條線,代表風險均衡組合的「縮放」,也就是槓桿。當我們想要達到某個報酬時,只要調整槓桿即可,而且因為是線性增減,我們可以得到比原始MVO(無槓桿)更好的回報。
當然,用加槓桿的Risk Parity,來打敗沒加槓桿的MVO,勝之不武。我用另一種說法解釋,不管我們利用何種優化方法,都希望策略本身的「風險調整收益」高,也就是盡量低風險高報酬。至於原始組合的收益如何,其實沒什麼影響,反正我們都可以利用槓桿解決。既然如此,有些投資者相信,根本不必要將收益當成參數進行優化,因為只要夏普率夠高即可。(Sharpe是評估風險和報酬方式之一。) 所以與其使用對參數敏感的MVO,不如使用讓投資者較有信心的Risk Parity.
4. 想要均衡配置風險,怎麼執行呢?
最簡單的,應該是把風險平均分配,也就是「等風險分布」(ERC, equal risk contribution). 當然,風險有很多種解釋,除了常見的波動外,也有人用VaR(風險價值)和ES(期望損失)等。這裡為了便於理解,我用傳統變異數來解釋。至於偏微分部分,也是形容風險的一種方式,和Euler定理有關,中文是「邊際風險貢獻度」(marginal risk contribution, MRC/MCR).
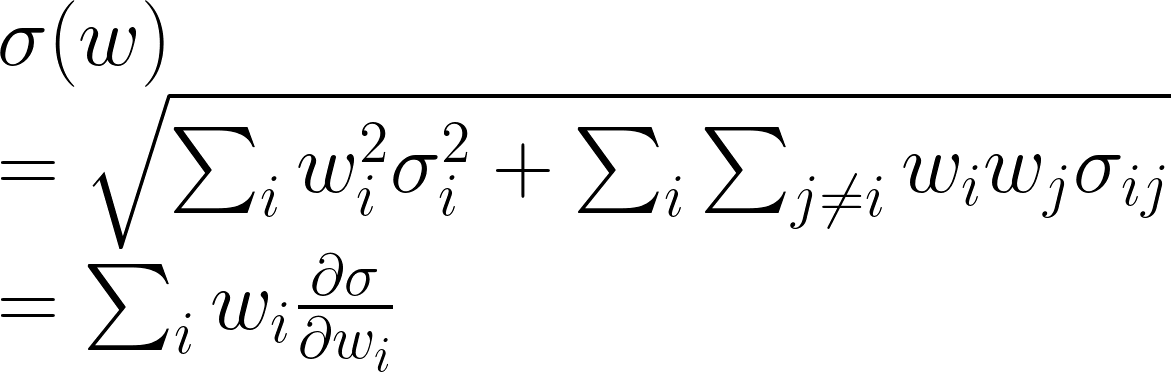
我們也可以寫成個別資產的權重形式。
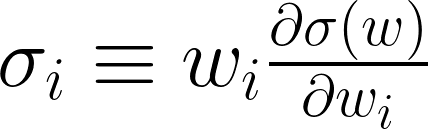
既然現在要「風險等權重」,那我們就要讓 wᵢ(Σw)ᵢ 和 wⱼ(Σw)ⱼ 一樣,其中Σ是協方差矩陣,這個形狀大家應該在Markowitz的理論中看過。接著,我們把目光放到求數值解,並加上一些約束條件。
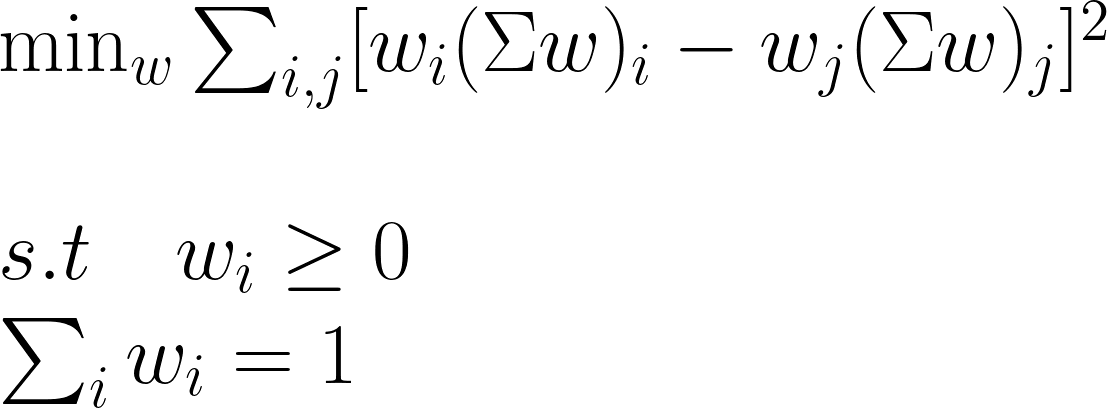
現在,只要用各種演算法「逼近」數值解,我們就可以知道資產的對應比例。
5. 作為對比,我們來看看風險平價(如ERC)的好兄弟。
由於ERC的波動包含了wᵀΣw,這不禁讓我們想起老大哥MVO。事實上,它們還真的有血緣關係。
先回憶一下MVO的形狀。
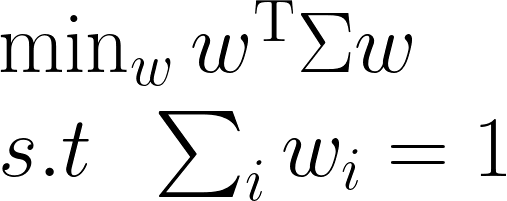
再次召喚Lagrange,這邊只考慮一個約束和對應的λ.
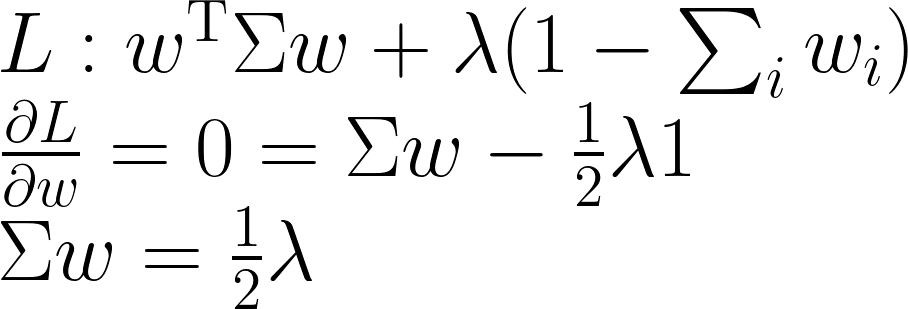
由此我們知道,這些λ和對應的Σw是相等的。換句話說,MVO把Σw均衡化,而大家也別忘了,Σw又是MRC的產物。所以從這個角度來看,MVO和ERC的行為非常相似。
另外,還有一種「最小方差法」(Minimum Variance),構建原理和MVO, ERC有相似之處。
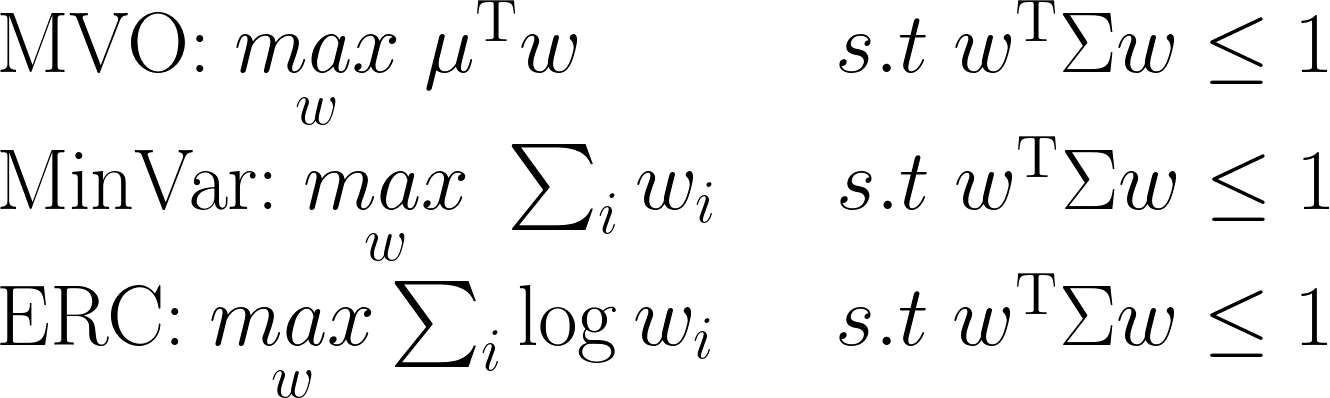
實務上,這種形狀的問題,可以利用二階錐算法(second order cone)來解,像Matlab就有它的求解程式。
定性來看,如果我們把資產簡單均分(1/N),那就是不考慮預期收益、共變異數和組合方差;而如果我們使用MVO,就是利用所有參數來最優化。至於ERC, MinVar和類似做法,是在兩者之間的某處找到平衡,因此它們的求解步驟長得很像。這類最優化方法系出同門,而要使用何種分支,端看投資者想要強調的部分。
如同我在介紹衍生性商品時所闡述的,人類的決定比工具還重要。我認為投資人不了解背後原理和配置目標,一昧利用程式把參數最優化,只會求出很精美的垃圾結果,對於實戰沒有幫助。(除非妳是老師,有表演需求。) 大家不妨思考各種優化工具的異同、自己的投資風格和能力以及前人的失敗和突破,才能立足巨人的肩膀。
6. 恭喜各位進入獎勵關卡,妳知道MRC怎麼推出來的嗎?
如果c是常數,而f(c‧x)=c‧f(x),那麼我們叫它一階齊次方程(homogeneous of degree 1)。我們可以發現,不論是投資組合收益Rₚ、加權預期收益μ還是組合波動σ,都是一階齊次。其中關於σ的矩陣形狀,已經出現過許多次。
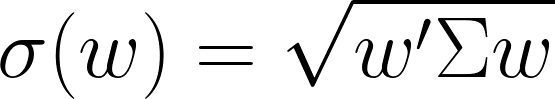
注意w'就是wᵀ,代表轉置矩陣。
Euler定理,適用於連續可微一階齊次方程。
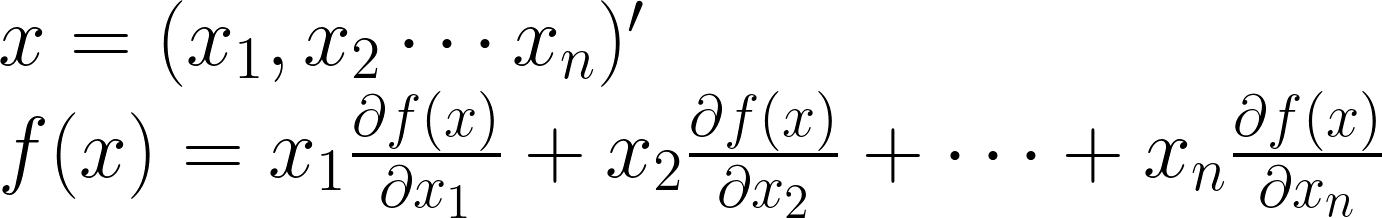
現在,假設風險可以用標準差來形容,我們就將兩者合併。
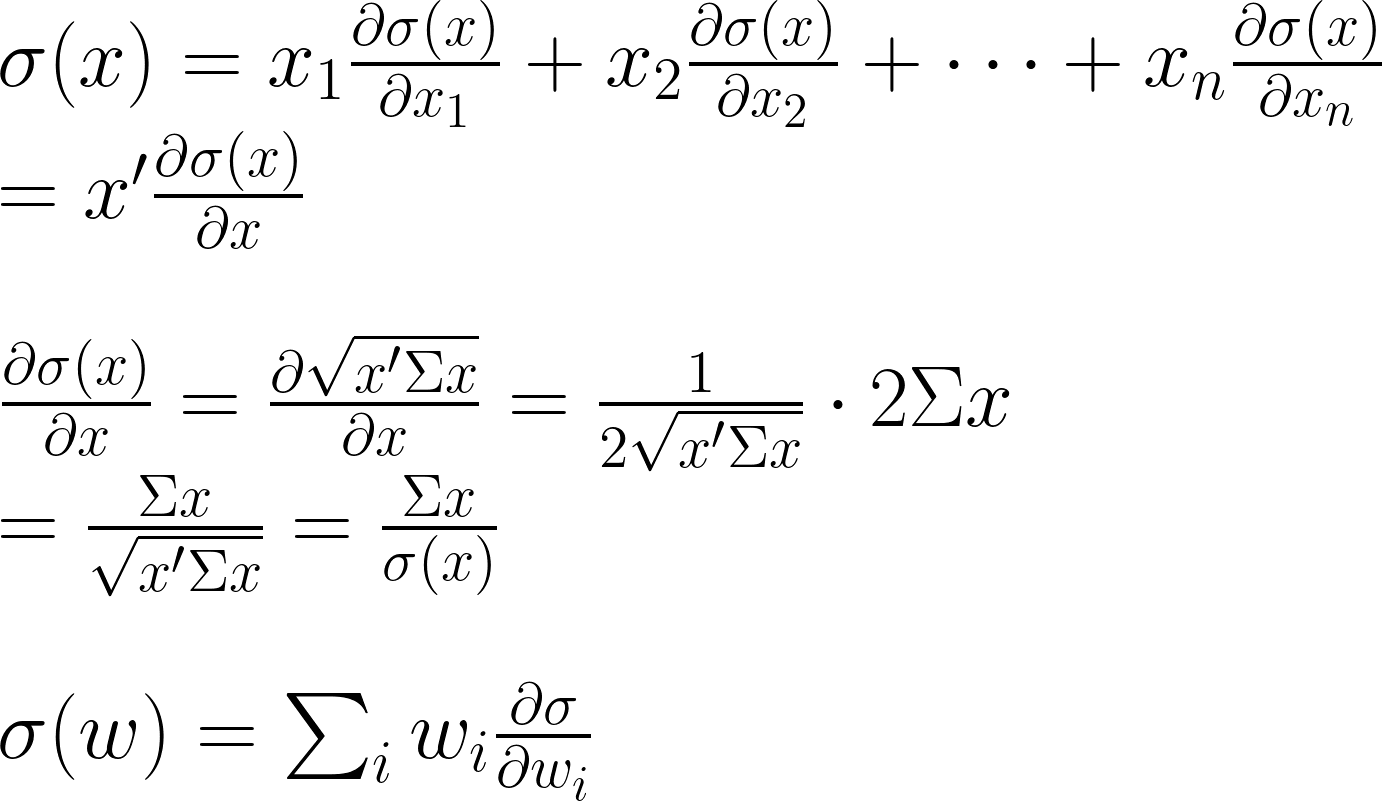
求導用到連鎖律。我們可以看到,透過Euler定理,可以推導出偏微分形式的MRC.
7. 等風險權重的基本形式說完了,不過風險平價還有許多可以探討的地方。
最讓人頭大的,是關於「協方差矩陣Σ」本身。前面提到,在風險平價模型中,可以考慮資產間的相關性而求得權重,畢竟很少有資產彼此完全不相關。然而這個相關性,是原始等風險權重算法的致命傷。舉個例子,如果有兩個資產完全相關,就會因為風險相同,而被分配到一樣的權重,加起等於單一資產的兩倍,但這顯然違背了風險均衡的理念。
另一方面,由於投資人普遍會為風險均衡策略加上槓桿,這就需要考慮到風險調整報酬,例如Sharpe. 那問題來了,我要先ERC再槓桿,還是先槓桿再ERC? 如果我進一步考慮相關係數和Sharpe, 我又需要做什麼調整? 關於槓桿本身,是要保持不變還是動態調整? 而再次提及風險,有人用傳統標準差,有人用VaR,有人用ES,也有人用橢圓分布模型,那麼這些衡量方式會如何影響風險預算?(Risk Budgeting)
考慮到波動率控制,就同時需要知道不同風險預算的差異、風險調整報酬和槓桿,我就看過不少人把ARCH家族拉進來討論。而考慮到預期報酬,雖然在Risk Parity裡面比較少被提到,但如果結合Black Litterman,剛好可以避開對市場完全有效假設的陷阱。
這些問題,或許投資人遲早會遇到,也都有人在研究。因此如果妳看到這裡覺得有趣,不妨也去找相關資料來研究吧。
回頭看看風險均衡的概念和全天候基金,Dalio等基金經理並不完全依靠資產波動來決定權重,而是融合主觀判斷來配置資產。如果各位想要迅速複製出一組「資產每天偷偷長大」的全天候策略,我提供常見的配置比例,各位可以輕鬆使用ETF投資。當然,投資一定有風險,妳抄作業虧錢可以來找我,但我不會負責,而且我會笑妳。
美股大市值 (VTI): 30%
美債長期 (TLT): 40%
美債中期 (IEI): 15%
黃金 (IAU): 7.5%
商品 (PDBC): 7.5%
註: 感覺還有很多沒寫到的,但考慮到篇幅,就把資料出處都放在文末,供各位讀者參考。
本來只想講故事,結果最終還是加入了數字。
我在Markowitz那篇「不小心」把數學推導寫進去,開了罪惡先例,導致後面好像不來點算式都怪怪的:)
開玩笑的,這些理論本來就都有關係。
沒有MVO,哪來CAPM?
MVO要是沒有對收益「過敏」,有人會想發展BL模型嗎?
我從選擇權BS說到槓桿和波動,是為了給風險均衡鋪路。
就如同我提到Bayse機率,是為了方便介紹BL模型。
想來也好笑。
當初,我只是想要介紹一篇論文,提到BL+風險平價+因子配置的擇時,後來一不小心寫成了資產配置系列。
結果現在我反而覺得那篇文章不這麼重要,因為讀者如果都能熟悉工具的用法和背後原理,自己就會打出組合技了。(至少在腦海中)
考慮到系列的推進和脈絡,我決定刪減掉部分內容,包括Barra的介紹。
換句話說,我下一篇很可能出「因子投資」文章,也總算比較接近我的階段目標了。
先預告,目前我的做法是只寫定性討論,盡量不放數學算式,當然具體細節還是要全部寫完才知道。
如果你等不及了,可以先去看一本《因子投資》,我也寫過書評。
關於本文,如果我哪裡寫錯或是說不清楚,歡迎告知。
參考資料:
- 北京大學數學科學學院 系統化資產配置系列之七: 基於目標波動率的風險平價改進策略
- 華泰證券 風險平價模型的常見理解誤區剖析
- 臺灣指數股份有限公司 指數編製方法概論
- University of Washington, Eric Zivot, Portfolio Risk Budgeting
- Advances in Portfolio Risk Control: Risk! Parity?
- The All Weather Story
- Risk Parity Portfolios: Efficient Portfolios Through True Diversification (PDF)
- Risk Parity Fundamentals
- Quantitative Equity Portfolio Management: Modern Techniques and Applications
- Euler Decomposition
- On the properties of equally-weighted risk contributions portfolios
- Optimal Versus Naive Diversification: How Inefficient is the 1/NPortfolio Strategy?
- Enhancing Risk Parity by Including Views
- Are Risk-Parity Managers at Risk Parity?
- Equal Contributions to Risk and Portfolio Construction (PDF)
- Introducing Expected Returns into Risk Parity Portfolios A New Framework for Asset Allocation
- Our Thoughts about Risk Parity and All Weather
- Risk Parity and Beyond - From Asset Allocation to Risk Allocation Decisions
- The Properties of Equally Weighted Risk Contribution Portfolios
- 還我兩顆地球
- Black Litterman 資產配置的好武器
- Markowitz和效率前緣
- 狂徒書評 〈因子投資〉 金融界的分子料理(Vocus)
