【讀paper】#1 投票與喜好之間的距離
*作為一個想要唸經濟學博班的經濟學入門仔,在Matters的第一篇文章,就從讀paper的筆記開始吧。
摘要(太長不看版): (1)理想中的投票機制,期望將民眾的偏好轉換為誠實的選票,再將選票轉換為選舉結果。投票機制的設計,既要考慮到如何處理「選民投票與喜好不一致」的問題,也要考慮到「在預期選民會『含淚棄保』時,選舉結果能否真實反應大眾期望」的問題。 (2)法國投票制度是兩輪選舉制。這個制度設計中的臨界值,可以讓研究者通過計量經濟學方法(RDD)清楚地看到「堅持選擇自己愛的候選人」和「策略性地投給有希望贏得選舉的人」兩組投票行為帶來的影響的差別。 (3)「堅持選擇你愛的」,在法國投票的例子中,會改變五分之一的選舉結果。 (4)斷點回歸設計,簡稱RDD,是一種模擬實驗的數據處理方法。在某些條件下,利用這種數據處理方法,研究者有能力回答因果關係的問題。
嘗試淺顯易懂的前言:
從前我以為經濟學是研究金錢的所以覺得很無聊(好天真!)
誤打誤撞跳入經濟學坑後,現在我對經濟學的理解是:
嘗試著以一種嚴謹的計量方法去闡明人類行為決策中的因果關係(超吸引人吧!)
因果關係這件事非常有趣,仔細思考過後你就會發現,日常生活中我們本來以為的因果關係很多情況下都是假的,是未經控制的、在經驗下得出的結論。
比如某天你頭痛,飯後吃了阿斯匹林,一個小時以後你的頭痛好了。在這個例子中,我們可以說「因為吃了阿斯匹林,所以我的頭痛好了」嗎?經濟學家的答案是「不能」。
在以上的例子裡,你完全沒有辦法排除,是我的頭痛自己好的/我吃過飯所以頭痛好了等等所有的可能的選項。你得到的只是相關性,並不是因果性。
所以我們可以怎樣得到因果關係呢?
在想像的世界中,我們需要一個你和一個平行世界中的你。平行世界指的是,兩個世界中的條件都一模一樣,除了,現實世界中的你吃了藥,平行世界中的你沒有吃。
如果在這個情況下,現實世界中的你頭不痛了,可是平行世界中的你依舊頭痛,我們才可以得出「吃阿斯匹林是頭痛消失的原因」的結論。
可是暫時,我們沒辦法去到平行世界做研究。*<1>
所以經濟學家在現實中能做到的最好,就是「隨機實驗」,即,嘗試用兩組足夠多的人中的隨機性,去平均掉除了我們感興趣的「處理」以外的因素的差距。*<2>
但在無法做到隨機實驗的現實生活中,經濟學家們就需要花心思去想各種各樣的方法去接近「隨機實驗」的狀況,嘗試說服讀者,在這樣的數據處理方法中,我們看到的差距基本上來源於我們關心的問題。
在等下要讀的paper裡,作者用一種叫做斷點回歸設計RDD (Regression discontinuity design) 的方法去模擬一個隨機實驗。 雖然我們關心的很多事都是個人選擇帶來的影響,例如說,如果我們關心有沒有進入台大(類似於香港的港大港中文,以及大陸的清北)唸書對一個人未來收入的影響,很難釐清台大學生和其他學校學生的收入差異是由「台大」本身帶來的差異,還是存在著其他我們看不到的(比如努力程度或者智商等等)的某些內生的因素影響。(i.e.台大出來的學生收入高,可能是他們本身能力就強,而與有沒有上過台大無關。) 為了分離「內生的某些能力」和「台大經歷/學歷」的因素,我們可以只看「差一分上台大」和「剛剛好多一分上台大」的這兩群人。他們是否有「台大經歷」存在著一定的隨機性,除了「命運指使剛好差一點有沒有上台大」,其他的特質可以在足夠多的人群中平均掉。這樣,兩群人的收入差異可以被認為只是由於「台大經歷/學歷」帶來的。 這種只看「臨界值左右一小段」並且對比臨界值左右的差異的方法,就是RDD。
今天讀的是Econometrica的2018年的一篇政治經濟學*<3>的paper:
在民主世界中,權力的限制來源於競爭與制衡,而當權者的執政合法性來源於人民的選擇。所以,投票的機制設計,是一件非常重要的事。
在理想的代議制民主制度下,一個設計好的投票機制,應該完成的是:
a)將選民內心的喜好轉化為他們的選擇:從偏好(preference)到選擇(choice);
b)讓收穫最多選民的認同的人當上總統:從選擇(choice)到結果(outcome)。
這個過程看似容易,但是操作上卻存在著各種各樣的困難。
比如說:選民真的可以只按照他們的喜好來投票嗎?當你支持的人排名第三的時候,你是會依舊選擇「你最支持的人」(i.e. 鐵桿粉絲投票)還是「看上去有機會贏的人裡你相對更喜歡的那個」(i.e.策略性投票;台灣的同學跟我講這叫「含淚棄保」)?
那在我們無法保證偏好可以完全轉換為選擇的情況下,要怎樣去設計投票機制,才會選出一個更符合大多數人偏好的候選人?
在法國的「兩輪選舉制」中,因為制度設計中的臨界值,我們得以用上述提到的RDD方法,去看到一些有趣的結果。
法國兩輪選舉制規則(如下圖):
第一輪:選民可以投給自己支持的候選人。
第一輪中得票率最高的前兩位自動進入第二輪,而第三位是否進入第二輪,則需要看他在第一輪的得票率是否高於12.5%
第二輪:選民可以投給進入第二輪的候選人。
多數決,獲得最多支持的候選人贏得選舉。
首輪直接當選:難度非常大。
需要得票數多於 (1) 所有候選人所得到的票數的50% (得票率 >= 50%);(2) 合格選民數的25%
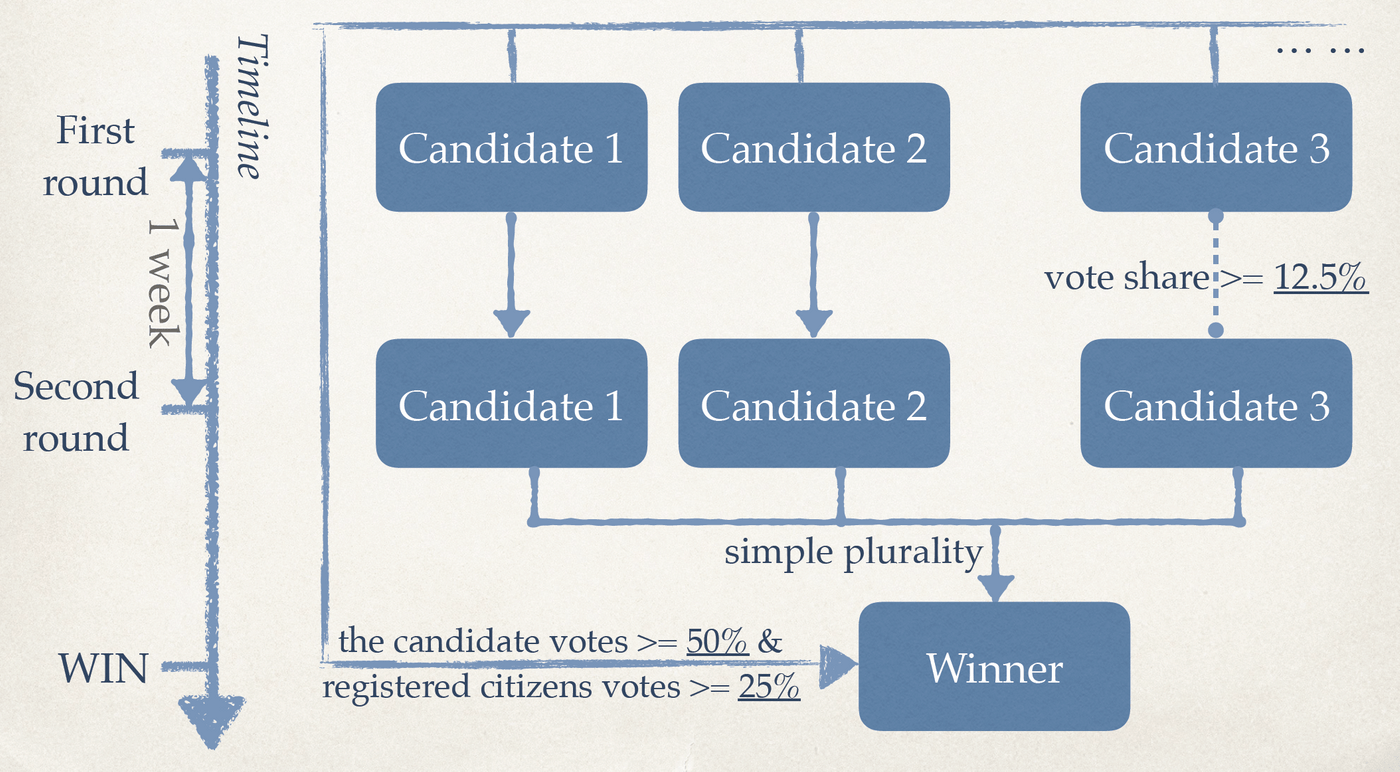
在這樣的制度設計下:
對於第三名候選人的支持者來說,如果第三名候選人成功闖入第二輪,他們可以選擇「策略性投票」(預期第三名勝面不大,選擇前兩名中自己沒有很喜歡的那一個)或者「鐵桿粉絲投票」(不管怎樣,堅持投給自己支持的第三名)。
但如果第三名沒有入選,除了(少部分的選民會)棄票,他們只能選擇「策略性投票」,沒有辦法堅持「鐵桿粉絲投票」。
透過支持第三名的選民第二輪的兩種情況的分流,我們關心的「選民的投票是否是策略性的」這件事情對投票結果的影響,可以透過「第三名候選人是否晉級第二輪」對選舉的影響來窺知一二。我們可以檢驗「策略性投票」、「鐵桿粉絲投票」的各類選民是否真實存在;如果是,存在的程度和範圍如何;並且,不同的投票方式的選民會怎樣影響選舉的結果。
在前言裡,我們介紹了一種叫做RDD的方法,它利用在臨界值左右分配的隨機性,試圖模擬一個隨機試驗,來回答在臨界值前後的差異為何的問題。在我們的法國選舉的例子中,得票率在一個小範圍內的分佈可以被看成是隨機的。因為選舉中很難對投票率進行操控,所以實力/支持率相近的一群人(i.e.「第三名候選人在第一輪投票的得票率」在12.5%左右的樣本),究竟有無進入第二輪可以看作是隨機的。此時,我們看到的影響可以被認為是「因果關係」。
作者發現,「第三名候選人晉級第二輪」這件事:
(在作者調查的橫跨37年577個選區7257場選舉的data的平均值)
1. 使得總投票率上升4.0%
因為存在一部分第三名候選人的忠實支持者 (loyals) ,他們只投給第三名,如果第三名候選人沒有第二輪的資格,就不會出來投票。這群忠實支持者是總投票率上升的主因。
2. 其中,空白票和廢票率下降3.7%,有效票上升7.8%
第三名候選人有資格,使得他們的忠實支持者為表抗議而故意投下無效票的比例降低,相應的,有效票的比例也因第三名候選人的加入而增加。
3. 第三名候選人的加入使得前兩位候選人的得票率下降6.9%
另一些選民,被定義為「游離選民」(switchers) ,他們的策略是在第三名有資格時投給第三名,當第三名沒有資格的時候,就會在一二名中選擇一個。這群游離選民的存在是前兩位候選人得票率下降的主因。
在第三個結果以後,作者進一步探討了更有趣的問題,那就是:第三名候選人的加入引起的前兩位候選人的得票率下降是成比例的嗎?如果不是,那麼第三名候選人的加入,是不是可能造成選舉結果的改變?
答案是:不是。
作者接下來定義了候選人的政治傾向,用(極左、左、中、右、極右)幾個傾向去劃分候選人。最後發現:
4. 當第三名候選人於前兩個候選人中的任意一個傾向一致的時候,大部分情況下 (91.1%) 第三名候選人傾向於退出第二輪選舉。
5. 在第三名候選人於前兩個候選人傾向均不一致的時候,大部分(85.2%) 第三名候選人傾向於參與第二輪選舉。
6. 第三名候選人的參與會搶走政治傾向離他更近的候選人更多的選票,在近五分之一(19.2%) 的情況下,改變選舉的結果(i.e.在第一輪中排名第一的人,因為和第三名候選人政治傾向更相近,爭奪選票,在第二輪中輸給本來排名第二的候選人)。
此外,作者還定義了進入第二輪選舉的候選人的實力 (strength) 。在第一輪選舉結果已知的情況下,進入第二輪選舉的候選人,應該期待自己得到所有跟自己政治傾向相同的候選人的票。所以作者將第一輪中,和第三名候選人政治傾向相同的候選人的得票率相加,定義為他的實力。
結果發現:
7. 第三名候選人的實力,對選舉結果造成的影響並不顯著。這說明,第三名候選人決定是否參選,並不一定是看中獲勝的機率或者是對選舉結果造成的影響,反而更可能在意,「參與第二輪選舉」這件事本身,給他帶來的好處(比如名聲、曝光機會等等)。
在這樣的結果中,我們可以證實「策略性選民」和「鐵桿粉絲選民」的存在,並且發現,在我們的樣本中,這種「鐵桿粉絲選民」的投票大約會改變五分之一的選舉的結果。
或許現實生活中,策略性投票永遠會存在在任何一場選舉中,這種擁有多數支持的候選人應該當選的邏輯也存在著一定多數暴力的問題。只是,去探討何種的選舉模式才是更合理的、去回溯過往選舉中發生的事情,永遠都是重要的、有趣的議題。
今天的讀paper時間就到這裡啦。
這只是我的第一個嘗試,斷斷續續改了很久,可是也許還是很稚嫩,也或許依舊有錯誤(歡迎指出!)但我總有一些做科普的理想,雖然還不那麼擅長,但也要開始嘗試才會慢慢進步。
附註:
<0> 感恩我的世界第一可愛室友@食芒果 、政研所同學安噗噗、孟章學長給本文的大力協助。之後實在抱歉我一直刪來改去,又遇到一些擾亂心緒的事情,所以不小心拖了有點久。
<1> 前言中阿斯匹林的邏輯其實被更廣泛的應用在自然科學的統計學中。經濟學家在這些釐清因果性中的特殊點大概在於我們更加在意用複雜的計量方法去探討因果關係在現實中的複雜性。
<2>所以有一個非常可愛的經濟學分支叫做實驗經濟學~嘗試去用隨機實驗的方法去得出因果關係,那就是我在做的事情啦~(超級有趣!感興趣的同學可以去估狗「實驗經濟學」)
<3> 政治經濟學這個詞有比較特殊的歷史背景,在不同學科發展中被賦予了很多不同的意思,為了消解歧異,這裡特指:用經濟學的方法去研究政治,i.e. 用賽局理論的模型去分析政治現象/用數理化的計量模型去分析政治現象的數據得出結論。
