[Python] Process simulation of the wave function of particle(electron) in a box
Assume there is an electron in a 1-dimension infinite potential well, and its initial state is the wave pocket whose center is at x0 = L/2:
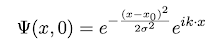
In this expression, L = 10−8m, σ = 10−10m, k = 5×1010m−1. Set other physics constants as h = 1.0546 × 10−34J · s,Me = 9.109 × 10−31kg.
Then, set the time step as ht = 10−18s and the coordinate step as hx = L/N. N = 1000 refers to the length L being cut into 1000 equivalent portions.
Here is the code:
import numpy as np
import matplotlib.pyplot as plt
#set parameters
L = 10.0**(-8)
sgm = 10.0**(-10)
k = 5.0*10**10
hbar = 1.0546*10**(-34)
Me = 9.109*10**(-31)
x0 = L/2
N = 1000
ht = 10.0**(-18)
hx = L/N
a1 = 1 + (1j*hbar*ht)/(2*Me*hx**2)
a2 = -(1j*hbar*ht)/(4*Me*hx**2)
b1 = 1 - (1j*hbar*ht)/(2*Me*hx**2)
b2 = (1j*hbar*ht)/(4*Me*hx**2)
#define initial state function
x = np.arange(0,L+hx,hx)
t = np.arange(0,2000*ht+ht,ht)
psi0 = np.exp(-(x-x0)**2/(2*sgm**2))*np.exp(1j*k*x)
#the matrix of the wave functions at different t
phi = np.zeros((len(psi0), len(t)),dtype=complex)
phi[:,0]=psi0
#set transfer matrix
A = np.zeros((len(psi0), len(psi0)),dtype=complex)
B = np.zeros((len(psi0), len(psi0)),dtype=complex)
for n in range(len(psi0)):
if n==0:
A[n,0]=a1
A[n,1]=a2
B[n,0]=b1
B[n,1]=b2
elif n==len(psi0)-1:
A[n,n]=a1
A[n,n-1]=a2
B[n,n]=b1
B[n,n-1]=b2
else:
A[n,n-1]=a2
A[n,n]=a1
A[n,n+1]=a2
B[n,n-1]=b2
B[n,n]=b1
B[n,n+1]=b2
#compute the wave functions
for n in range(1,len(t)):
phi[:,n]=np.linalg.inv(A) @ B @ phi[:,n-1]
#drive curves
for m in [0, 300, 500, 800, 2000]:
prob = phi[:,m]*np.conjugate(phi[:,m]) #compute the probability distribution
lbl='t='+str(m)
plt.figure(1,figsize=(15,3),dpi=300)
plt.plot(x,np.real(phi[:,m]),label=lbl)
plt.xlabel('x')
plt.ylabel('real')
plt.legend()
plt.grid()
plt.figure(2,figsize=(15,3),dpi=300)
plt.plot(x,np.imag(phi[:,m]),label=lbl)
plt.xlabel('x')
plt.ylabel('image')
plt.legend()
plt.grid()
plt.figure(3,figsize=(15,3),dpi=300)
plt.plot(x,np.sqrt(prob),label=lbl)
plt.xlabel('x')
plt.ylabel('probability')
plt.legend()
plt.grid()
Output:
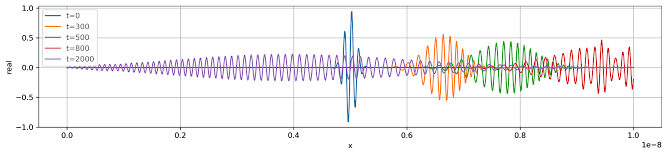
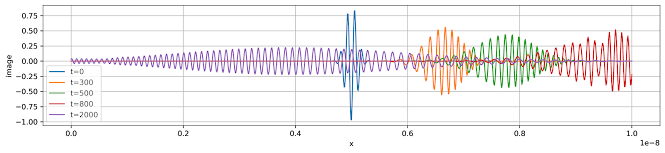
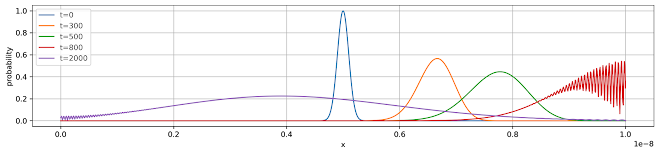
The running time is kinda long. Be patient.
喜欢我的作品吗?别忘了给予支持与赞赏,让我知道在创作的路上有你陪伴,一起延续这份热忱!
