槓桿ETF適合長期持有嗎?

★★★☆☆

警告，這篇文章，可能會讓「指數投資」的內戰更激烈。
不過，我就是喜歡狩獵，我享受把逆風轉成順風的過程。

無論是指數投資基本教義派，還是自由指數投資派，都會強調降低成本、多元分散、長期持有、被動貼近大盤......這些我都聽過，也非常贊成。
然而一旦說到「槓桿」呢? 至少有一半的作者會反對。
這簡直是一面照妖鏡，把作者的思路都攤在陽光下。

身為邪教派神棍，我不會放過這個機會。
今天，就來談槓桿。

為了聚焦在槓桿本身，我要先排除投資工具層面的缺點，例如轉倉、點差、手續費、交易成本、追蹤誤差......等。
別誤會，這些因素確實都很重要，也會影響投資報酬，但是它們和槓桿都沒有直接關聯，所以不該被混為一談。
更精確的說，大家是在討論指數和槓桿，而ETF只是追蹤指數的一種工具。
因此，雖然我也鼓勵各位使用ETF投資大盤並設計資產配置，但是本篇文章的重點在於「槓桿」。

1. 起手式，槓桿ETF天生帶有「耗損」，會慢慢吸血。
我製作一張表格，供大家參考。

假設今天指數100，第二天上漲25%，第三天下跌20%，就會「回到原點」。
同時，其它倍率的ETF，雖然也從100出發，但全都還在虧損狀態，這就是「槓桿耗損」。

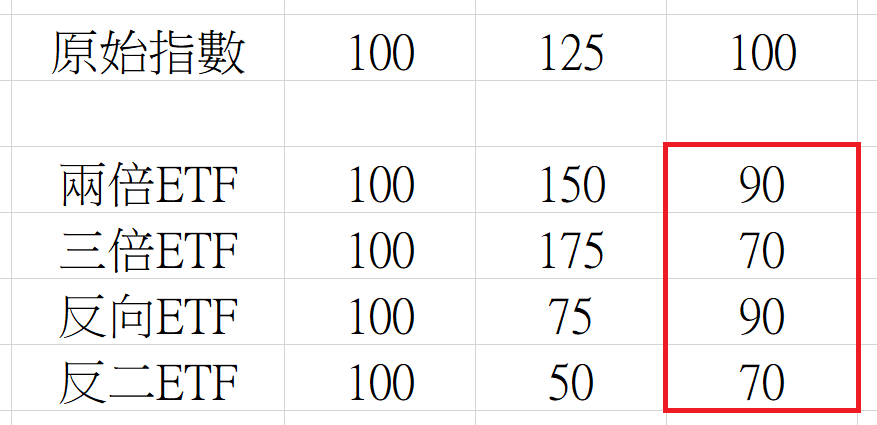
和封閉基金不同，ETF每天都能被公開買賣。
因此，槓桿ETF都是指「單日」槓桿，而不是長期槓桿。
用這個特性提醒投資者，我可以理解。
但是，後面的各種推論，就開始荒腔走板。

2. 有人說，只要有槓桿就不好。

答錯了。

槓桿代表倍率，所以一倍槓桿也是槓桿，空手就是零倍槓桿。
嚴格來說，每個投資環節都會帶有槓桿，只不過有些大於一，有些小於一，有些是負值。

股權本身有財務槓桿，債權更不用說。
市場上的交割、倉位、保證金等，全部都是可調整的槓桿。
政府縮表、加息、紓困、控制匯率...只要和金融有關，就天生帶有槓桿。
投資人該考慮的，是槓桿數值，而不是有沒有槓桿。

每個人喜歡的氣溫不一樣，大家可以討論。
但如果你的老師不願面對數值，只會堅稱今天沒有氣溫，那多半是基本教義派。

3. 退讓一步，有人認為，只要不是一倍槓桿，就會造成「耗損」。

真的嗎?

各位不妨思考0.5倍槓桿，或是50%資金的情況。
為了方便比較，我擴張原始表格。

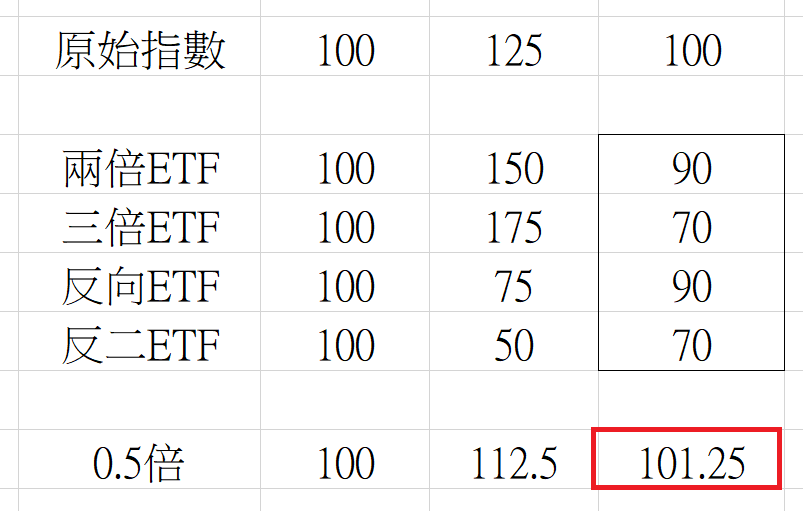
現在，各位意識到問題所在了嗎?

再退一步，有些人仍堅稱，槓桿一定會造成耗損，所以「零槓桿」會更好。
為了讓這些人死心，我一次從0倍做到0.95倍吧。

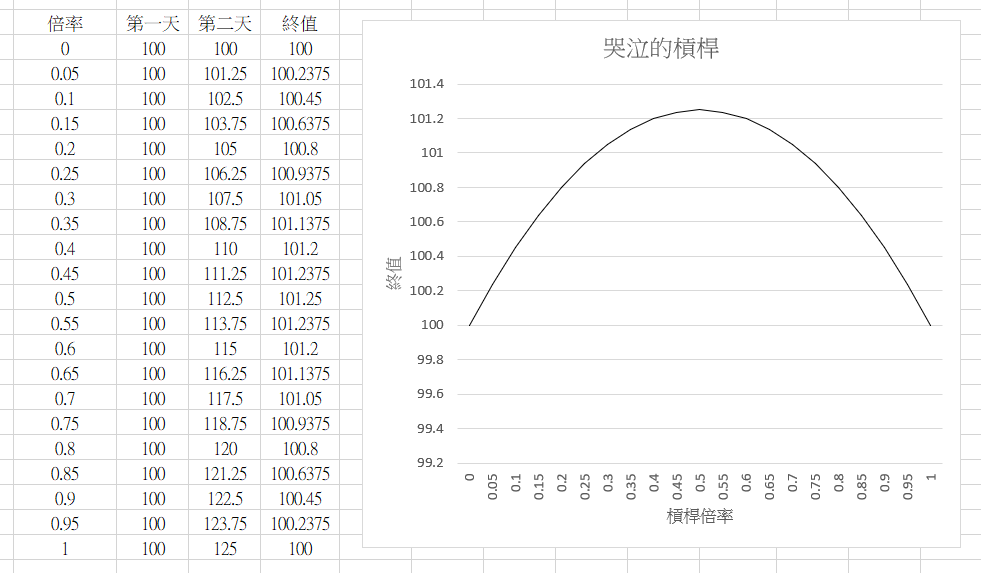
現在告訴我，「耗損」在哪裡? 怎麼越耗越多?
指數投資者喜歡提的「滿倉」投入，怎麼失靈了?
可別忘記，我是用你們設計好的耗損走勢，也把放大和反向槓桿都先排除了。

4. 如果堅定的信仰產生裂痕，我也達到目的了，不過我還想提醒各位一件事情。

越是基本教義派的指數投資者，越相信一個假設，也就是指數「長期上漲」。
那麼，精心設計的「原地」震盪盤，還有意義嗎?

不如，我採用比較合理的數字，重新模擬看看吧。
假設單日平均報酬0.03%(年化報酬7.7%)，波動約為上下1%，會發生什麼事呢?

乾脆一點，我使用100/99/100.06，直接從-1倍拉到5.5倍。

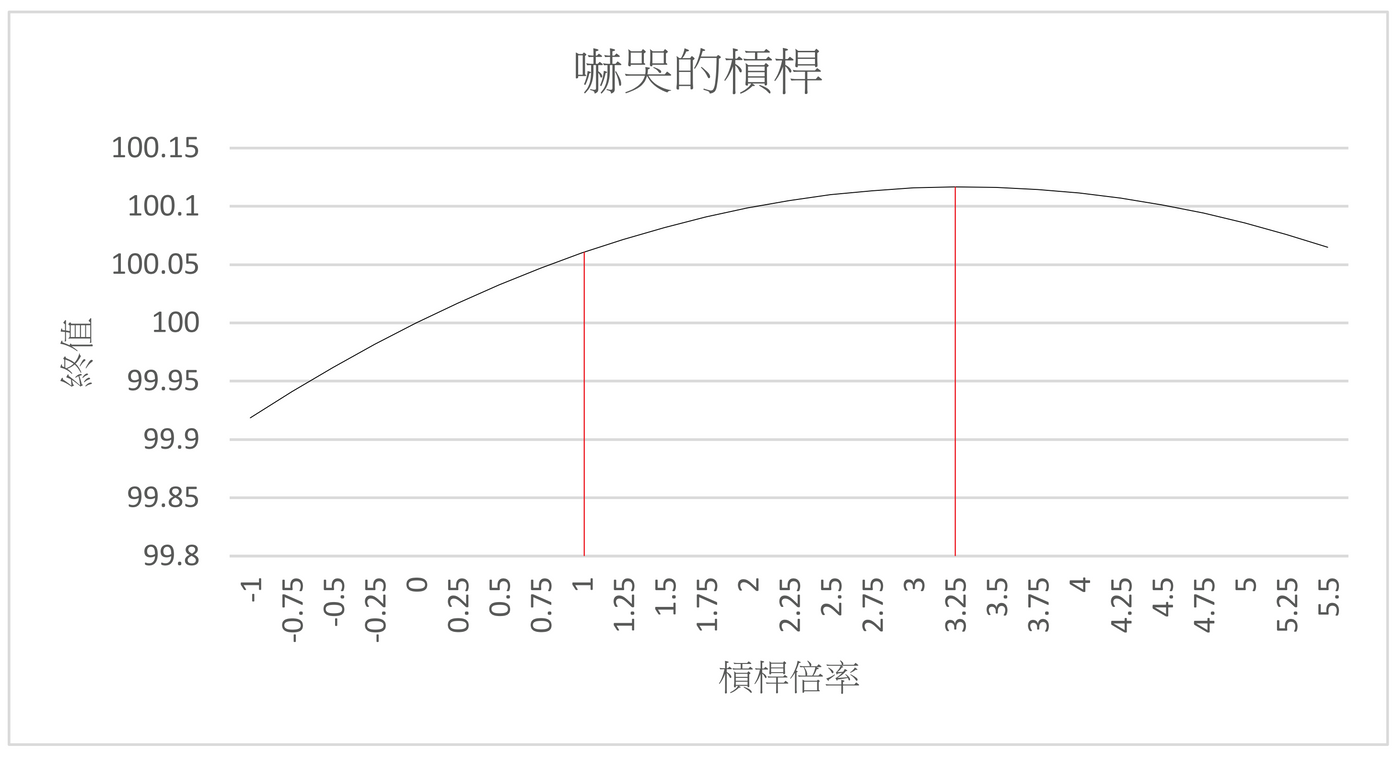
大家可以看到，在這個狀況下，3倍槓桿的表現比原始ETF還好。

如果各位喜歡，也可以自己模擬。
我為了節省時間而使用Excel，妳想跑Monte Carlo也好。

我認為，最佳槓桿率，會隨著波動和預期報酬，而坐落於不同區間。
越是震盪、原地踏步的指數，最佳槓桿會接近零；單邊走勢，最佳槓桿會離零較遠，例如+3或-3倍。

5. 話說到這裡，我要繼續深入，因為前面還有防線。

有些老師告訴讀者，因為槓桿耗損，所以長期持有槓桿ETF，「保證」追不到相應比例的長期報酬。
例如，長期持有兩倍槓桿ETF，最終的報酬會不到兩倍。

我說，這又是另一個謊言。
不過大家都會有無心之過，我就不點名了。

檢視前面的圖表，觀眾大概也知道，所謂槓桿和指數的關係，根本不是一個「定值」，而需要視情況而定。
所以，各位指數投資老師們，你可以從交易成本、心理因素或各種誤差的角度，提醒信徒謹慎使用槓桿型ETF，我認為這是負責任的表現。
但是，妳也最好先了解槓桿對投資的影響，做出基本判斷後，再決定是否跟著大家一起追殺「槓桿」。

我會在下一段說明長短期槓桿的關係，但我要先解釋一個現象。

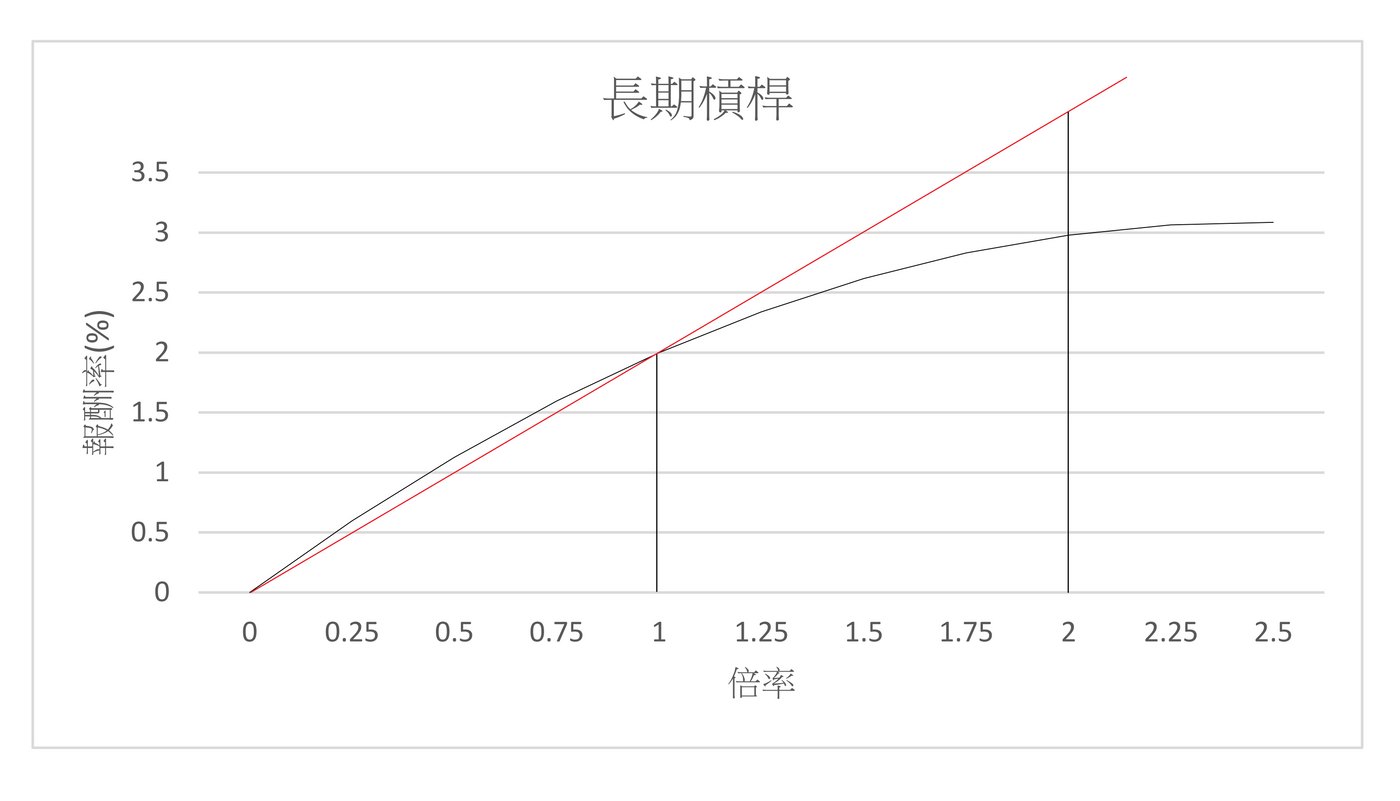
我過零點和一倍槓桿報酬，畫一條割線，然後比較拋物線上的數值。
大家應該可以發現，拋物線永遠低於斜線。
也就是說，單日報酬槓桿的累積，追不上報酬直接放大。

要證明也不難，把拋物線微分兩次就知道方向和最高冪次。
然而，這幅圖最多只能說明，當上下震盪頻率升高，「耗損」會拖累表現，概念接近幾何平均不大於算術平均(算幾不等式)。
至於最終結果，還沒有定論。

為什麼呢?

6. 來點數學。

我在〈還我兩顆地球〉中提過Ito積分，現在我要繼續說明，看不下去的讀者可以跳到下兩段。

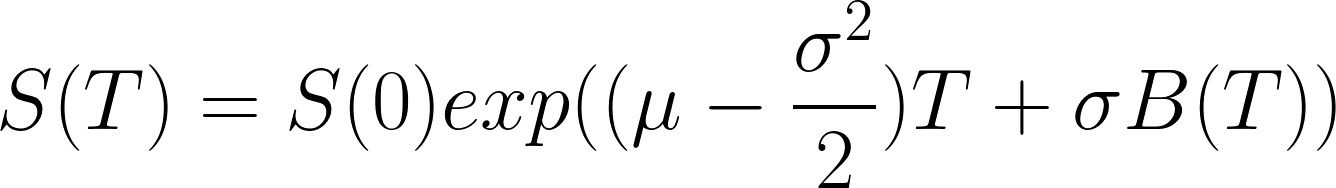
準確來說，我們先假設價格走勢符合幾何布朗運動(GBM)，此泛函的二次變分不等於零，但是三次以上變分全部為零。
如果讀者樂意，也可以考慮更高冪次的價格表示，它的原理接近Taylor級數。
我們暫時先考慮前二項，並以波動風險來代表槓桿，利用拋物線對標準差微分找出極值，會算出「最佳槓桿率」，出現在μ/σ²

另外，大部分的狀況，因為股票本身的波動分布特性，日度表現都是波動大而預期報酬小，如果套用回幾何報酬的表示式，幾乎都是「負的」。
這導致上述人工走勢案例，槓桿曲線都是「哭臉」而非笑臉，我們也可以將極值視為最大值。

There's a but.

雖然報酬率本身的幾何報酬比不上平均報酬，但是長期「價格」表現是一種連續乘法。
定性而言，如果報酬率呈現鐘形分布，回歸於均值，那麼累積起來的效果就會接近「指數成長」。(對，指數成長的指數。)
回頭看長期倍率，無論數值多大，只能是線性成長，所以早晚被指數追過。
也就是說，這種走勢會獎勵槓桿。

什麼意思呢?

如果我「設計」妥當，調配好時間、波動和預期報酬，我有辦法得出「笑臉」。
換句話說，我可以肆無忌憚的加上槓桿，而原本的最佳槓桿反而變成了最虧槓桿率。

我再次搬出人工走勢，並將槓桿率設定為-30倍到+100倍。
當然，我故意畫出負槓桿部分，是為了讓笑臉成形，實際上大部分的負槓桿都無法存活。

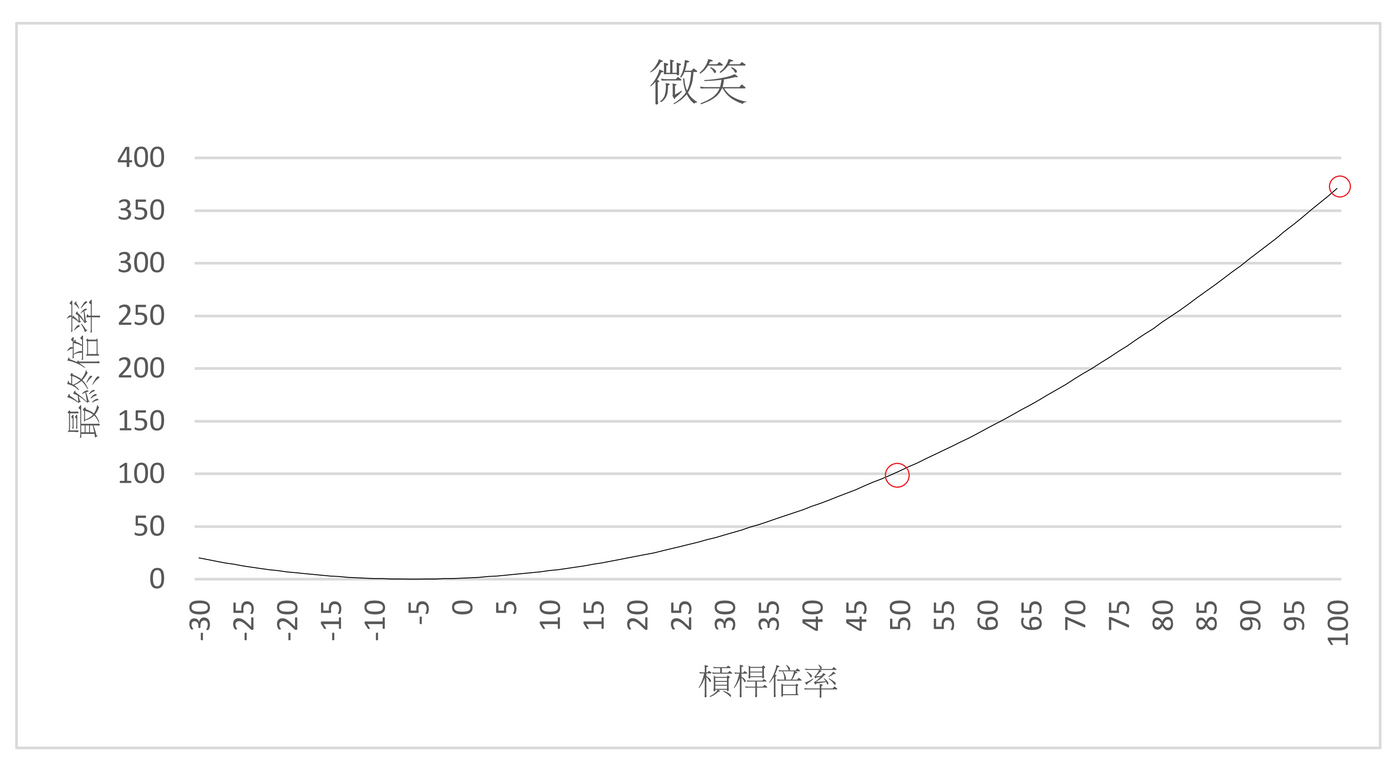
簡單解釋，當我用了50倍單日槓桿時，最終倍率已經到了100倍。
可是當我加倍槓桿後(50變100)，最終倍率變成350倍以上。
也就是說，單日槓桿不但可以勝過長期槓桿，而且理論上可以加入「無限」槓桿，會更划算。

實際上，我們根本不可能對股票上這麼大的槓桿，會瞬間爆倉，我會在之後解釋。
把笑臉放一邊，但也先不要轉台，因為我要繼續談統計。

7. 延續波動為常態分布的假設，我們先寫出PDF的樣子。

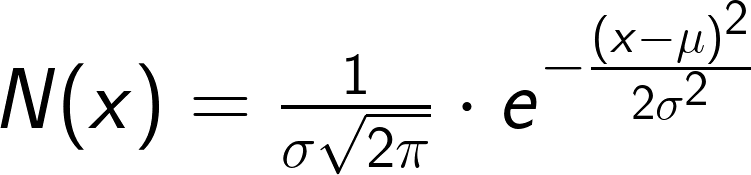
其中標準差σ和均值μ都是常數，可以暫時不管。
這裡的x代表波動，也是風險或槓桿的意思。
值得注意的是，μ是我們要的最終收益率(通常是好幾倍)，不是單期收益率。

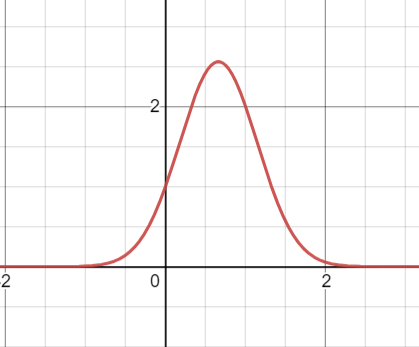
加上槓桿之後，我們可以為x量身訂做，分別對PDF的兩項公式動手腳，找出最後回報的分布。
具體「手術」內容就是使用幾何平均報酬表示最終倍率，並以x(1-x)表示成長的波動，安裝到e的冪次中。

參考The Dynamics of Leveraged and Inverse Exchange Traded Funds, PDF公式一樣是常態分布，只不過我們開始有對x施力的地方。

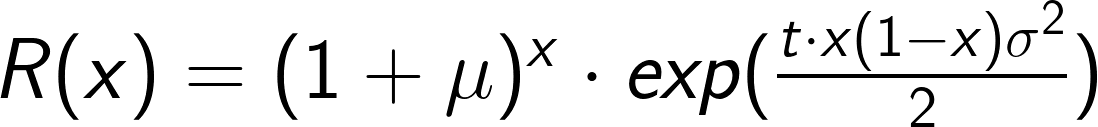
其中R代表回報，而t代表單位時間數，在此處是一天。

接下來，我把PDF對x偏微分，找出極值點。

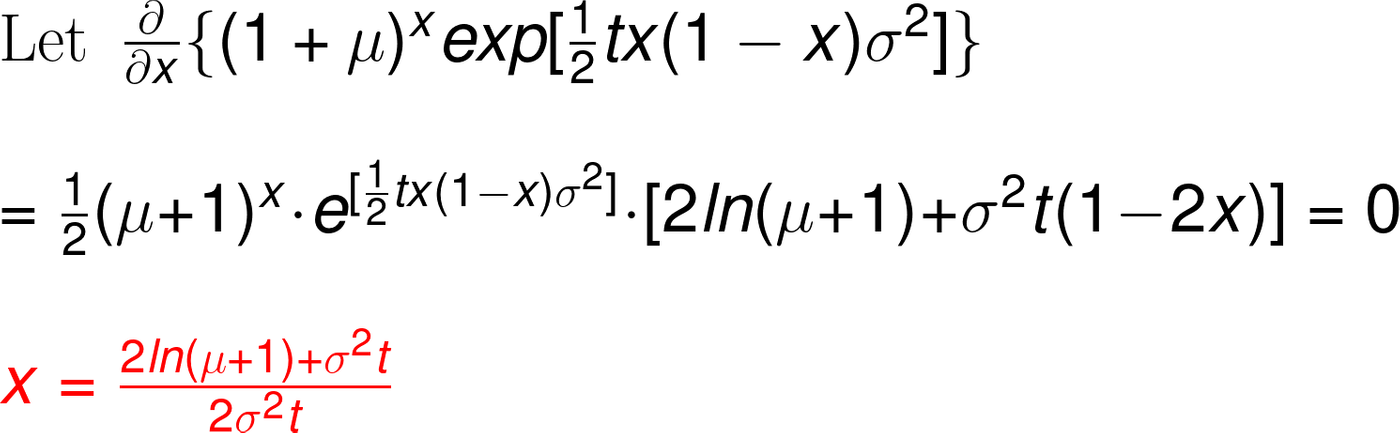
也就是說，此時的x倍槓桿，是考慮到了波動、時間、預期報酬和指數成長後，最有可能的數值。
如果你覺得有點眼熟，請相信自己。
紅色這個解，正是最佳槓桿率μ/σ²
我寫了一圈，是為了引進價格變化的機率分布，而數學上兩者的極值所在應該要相同。

8. 可能性最高的最佳槓桿率，我們已經知道了。
現在，來驗證理論吧。

道瓊指數，從1885年2月16號，至截稿前有約37480個交易日。日報酬的平均是24bps(0.024%)，標準差是1.07%，總共成長約1125倍。
依照前面的計算，得出最佳槓桿率約在2.1375倍。

在實驗之前，為了方便比較，我順便把2倍和2.5倍槓桿放在一起。
我們知道這會是「哭臉」，而且最大值會被另外兩組槓桿率包圍。

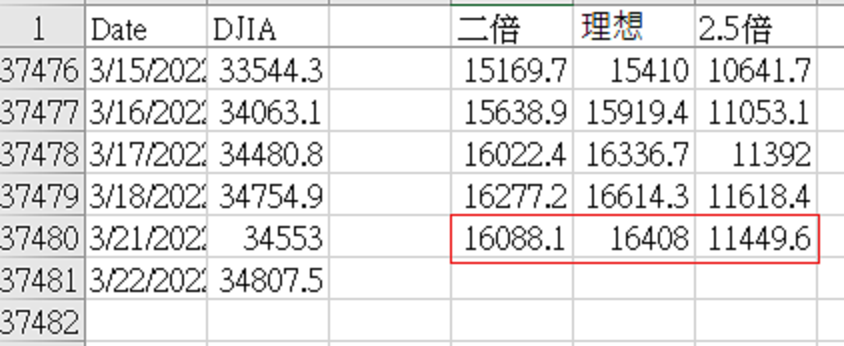
符合預期的，理論槓桿組的最終報酬也最高。
注意，我算出來的數字不是價格，而是「倍率」。

在指數本身成長1000多倍的前提下，最佳單日槓桿化有16000倍的表現。
雙倍槓桿或2.5倍槓桿，最終成長也都破萬倍。

我從19世紀放到21世紀，夠久了吧?
經濟大蕭條、兩次世界大戰、停滯性通膨、黑色星期一、科技泡沫、金融海嘯、歐債危機、美中貿易戰、COVID 19......每一次重大波動，都被槓桿放大。
結果，單日槓桿指數還是有10倍以上的領先。

在這裡，我就不說Who's your daddy了，讀者有機會可以自行對老師說。

9. 槓桿ETF和期貨的正確使用方法。

股市具有長期上漲但波動大的特性，因此絕大部分情況，都會有個最佳槓桿率(哭臉曲線)。
通常，最佳槓桿率會落在1的外面，但短期內有機會因為震盪而縮進0到1的區間，而如果是單邊下跌走勢，最好的槓桿甚至會出現在0的外側，也就是做空。

另一方面，有些非常穩定的資產，例如銀行現金或是債券，複利效果明顯，所以有機會產生笑臉曲線，也就是鼓勵投資人盡量上槓桿。
在市場上只要有利可圖，投資人就會大舉進入，所以TED或LIBOR變動不須太大，就能影響非常龐大的資金。
FED光是宣布調整利率幾個bps，就能造成幾兆資金的流動，而這些投資行為自然也牽涉到多組槓桿。

因此，資產特性不同，槓桿的用法當然也有差別。

在我「誤入歧途」寫投資文章之前幾年，我確實是用Excel「逼近」的方式，找出Nasdaq/Dow Jones/SP500/費半/Russel 2000等指數的最佳槓桿率(印象中Nasdaq的最佳槓桿落在2.3到2.7之間)，然後我也沒想很多，直接用很大的倉位投資槓桿ETF
當時我是用搭配的方式，湊出兩倍多的總槓桿。

雖然研究方法很土，但各指數的走勢大家也心裡有數，我算是意外賺了些泡麵錢。
後來我開始接觸因子和期貨，也成功把Excel拉到崩潰，再後來我就用程式跑了。

槓桿ETF和期貨各有好處，而且槓桿增長特性也不同，我認為嚴格來說兩者不能互相取代。
不過我們也不應對混沌系統精確求解，心裡有個槓桿概念就好，所以ETF和期貨混用也無傷大雅。

實際上，投資人必須特別注意的是「交易成本」，畢竟以上計算都是基於指數，而ETF(和指數期貨)的主要功能便是跟蹤指數。
如果手續費、經理費、管理費......太高，讓投資工具脫離基準指數太遠，很容易摧毀整個投資計畫。

至於怎樣的槓桿倍率才合適呢?

我認為，曲線告訴我們「過猶不及」和最佳區間，但各位最好不要去賭最佳槓桿率，事情總有出錯的時候。
所以實際上，我都保守的建議大家不要放太多槓桿。

20%到50%的額外槓桿，對於有收入或閒錢的族群，並不會造成致命打擊。
舉個例子，上次股災指數大概跌50%，而股債各半大概跌30%
如果妳用50%槓桿(正式來說是150%)，股債各半大概會跌45%，反而比純股票還抗跌。

萬一運氣不好，就用時間來換，指數也不會下市。
套用坊間老師的話，指數投資很簡單，就是「看對、下大、套住」。

10. 指數投資內戰

有人說，指數投資就像邪教，容不下任何異音。
我覺得這不是教徒胸襟太小，而是有人頭腦不夠好。

我曾經遇過槓桿理念類似的讀者，有些人用持續轉倉的方式投資指數，也有人搭配它能接受的槓桿ETF組合。
可惜的是，第一波攻擊者，通常正是指數投資人。

我知道，有些作者和老師從來都不是投資者。
而我，在成為寫作神棍之前，就已經用槓桿ETF持續投資指數了。
我不在乎看到此篇文章的各路老師有多資深、多富裕，只要妳們繼續人云亦云，用「我感覺」來傳教，就算在指數投資領域，我也不會客氣。

我喜歡的討論方式，包括理論、證據和實際經驗，而這也是我常採用的論述模式。
你可以因為個人偏好而擁護原型ETF，也可以用各類交易成本來指出槓桿ETF的吸血。
妳還可以教學生強制平倉線、保證金和穿倉，以及造成追蹤偏移的contango/滑點/轉倉等。
這些「知識」和宣稱都很重要，但是它們都不該成為否定槓桿的理由。

如果妳剛好是指數投資人，下次在圍剿「非正統」分支的時候，可以先思考一件事情。
真的有100%純血指數投資嗎?

我從不諱言自己的投資歷史，我也不怕大家知道我根本非科班出身。
破壞規矩是我的規矩，顛覆信仰是我的信仰。
所以一如既往的，如果各位認為我哪裡說錯了，歡迎踢館。

參考:

還我兩顆地球

無中生有或是槓桿損耗，指數與槓桿

The Dynamics of Leveraged and Inverse Exchange Traded Funds