關於機器學習:概述

2021 年 1 月 25 日

本質上是部分簡明神經網絡教程(微軟俱樂部整的)的筆記（逃

你有一個模型——或許它不是完美的（這不是鐵定嘛）反正它已經是這樣了——你可以拿他來做一些預測或者分類些什麼，這是你的目的。於是你扔去了一個數值之類的到模型裡面——初始化——於是這個你扔進去的玩意就開始在模型裡面向前計算，最後得到了一個數值，正巧的是：你知道你扔進去的那個玩意所對應的正確值——顯然和模型算出的結果有差距（損失），於是你讓這個損失值返回模型讓它反向計算對模型進行微調來使模型更趨近於完美——這就是機器學習的過程

舉個栗子

目的：猜到乙心中的數字；

初始化：甲猜5；

前向計算：甲每次猜的新數字；

損失函數：乙在根據甲猜的數來和自己心中想的數做比較，得出“大了”或“小了”的結論；

反向傳播：乙告訴甲“小了”、“大了”；

梯度下降：甲根據乙的反饋中的含義自行調整下一輪的猜測值。

這裡的損失函數是什麼呢？就是“太小了”，“有點兒大”，很不精確！這個“所謂的”損失函數給出了兩個信息：

1.方向：大了或小了

2.程度：“太”，“有點兒”，但是很模糊
or黑盒
目的：猜到一個輸入值，使得黑盒子的輸出是4；
初始化：輸入1；
前向計算：黑盒子內部的數學邏輯；
損失函數：在輸出端，用輸出值減4；
反向傳播：告訴猜數的人差值，包括正負號和值；
梯度下降：在輸入端，根據正負號和值，確定下一次的猜測值。

搭建一個神經網絡，給出初始權重值，我們先假設這個黑盒子的邏輯是：z=x+x2；
輸入1，根據z=x+x2 得到輸出為2，而實際的輸出值是2.21，則誤差值為2−2.21=−0.21，小了；
調整權重值，比如z=1.5x+x2，再輸入1.1，得到的輸出為2.86，實際輸出為2.431，則誤差值為2.86−2.431=0.429，大了；
調整權重值，比如z=1.2x+x2，再輸入1.2……

調整權重值，再輸入2……

如果誤差值是正數，我們就把權重降低一些；如果誤差值為負數，則升高權重

所有樣本遍歷一遍，計算平均的損失函數值；

依此類推，重複3，4，5，6過程，直到損失函數值小於一個指標，比如0.001，我們就可以認為網絡訓練完畢，黑盒子“破解”了，實際是被複製了，因為神經網絡並不能得到黑盒子裡的真實函數體，而只是近似模擬。

或者舉個打靶的栗子

目的：打中靶心；
初始化：隨便打一槍，能上靶就行，但是要記住當時的步槍的姿態；
前向計算：讓子彈飛一會兒，擊中靶子；

損失函數：環數，偏離角度

這裡的損失函數也有兩個信息：距離and 方向——所以，梯度，是個矢量！它應該即告訴我們方向，又告訴我們數值。

反向傳播：把靶子拉回來看；
梯度下降：根據本次的偏差，調整步槍的射擊角度。
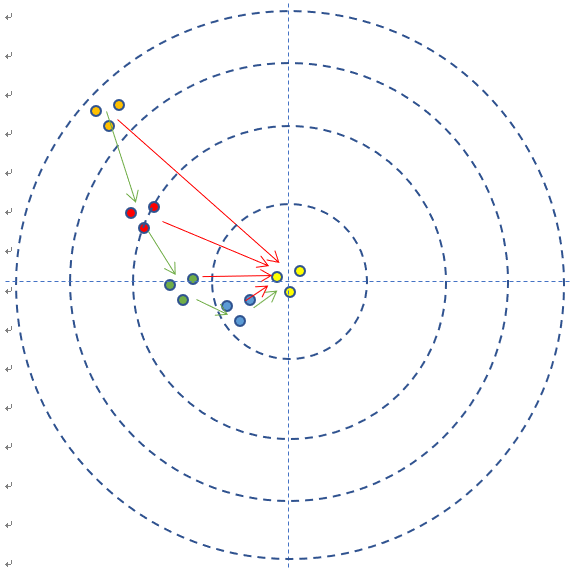
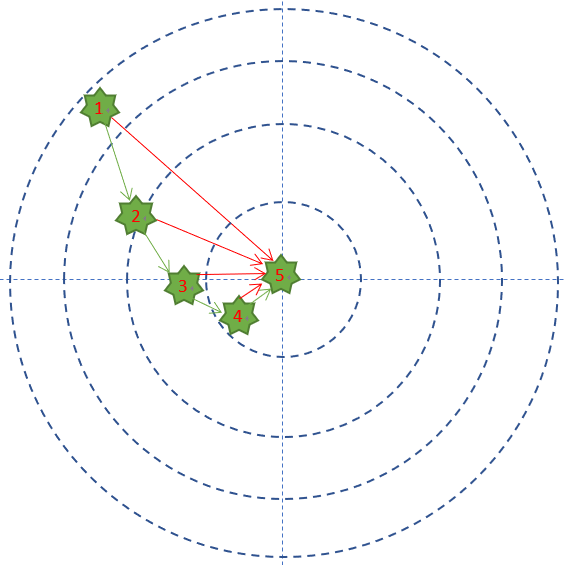
每次試槍彈著點和靶心之間的差距就叫做誤差，可以用一個誤差函數來表示，比如差距的絕對值，如圖中的紅色線。
一共試槍5次，就是迭代/訓練了5次的過程。
每次試槍後，把靶子拉回來看彈著點，然後調整下一次的射擊角度的過程，叫做反向傳播。注意，把靶子拉回來看和跑到靶子前面去看有本質的區別，後者容易有生命危險，因為還有別的射擊者。一個不恰當的比喻是，在數學概念中，人跑到靶子前面去看，叫做正向微分；把靶子拉回來看，叫做反向微分。
每次調整角度的數值和方向，叫做梯度。比如向右側調整1毫米，或者向左下方調整2毫米。如圖中的綠色矢量線。
在本例中，多個樣本可以描述為連發射擊，假設一次可以連打3發子彈（好傢伙直接霰彈），每次的離散程度都類似
如果每次3發子彈連發，這3發子彈的彈著點和靶心之間的差距之和再除以3，叫做損失，可以用損失函數來表示——在這個例子裡面，用得分來衡量的話，就是說小明得到的反饋結果從差9分，到差8分，到差2分，到差1分，到差0分，這就是用一種量化的結果來表示小明的射擊結果和目標之間差距的方式。也就是誤差函數的作用。因為是一次只有一個樣本，所以這裡採用的是誤差函數的稱呼。如果一次有多個樣本，就要叫做損失函數了。