[Outline of the History of Philosophy] Miletus School - Pythagorean School

Miletus School:

The first philosophical school of ancient Greece, represented by Thales, Anaximander, and Anaximenes, was mainly concerned with ontological issues in natural philosophy. Overall, the Miletus School did not break through the shackles of this world.

Thales:

Thales was the first philosopher in ancient Greece. He believed that "all things are born from water, and all things return to water." "Water" is the most basic "one" that makes up all things. Therefore, "water" as the source is different from other perceptual objects, and the relationship between "water" and other perceptual objects is "one" and "many". This concept was inherited by his assistant Anaximander and developed into the concept of "infinity".

Thales chose "water" as the source for the following two main reasons. First, as Aristotle recorded in "Metaphysics", "What promotes the growth of all things is damp... And water is the origin of the nature of wet things." The second is that the nature of origin is indeterminate, which is the infinite (indefinite/amorphous) we will mention later. Once the principle is determined to be defined, then the principle is no longer the beginning, nor is it the principle. Therefore, the form of "water" is not limited, it is more in line with the indeterminate nature required by the original.

Anaximander:

Anaximander was Thales' assistant, and Anaximander first proposed the concept of "primitive foundation" and "infinity". All things begin with the foundation and return to it. The connotation of infinity is unlimited, indeterminate, and in subsequent Elia school interpretations is understood as the meaning of infinity, without boundaries.

First of all, the concept of "infinity" is more universal than "water". "Infinity" does not come directly from the sensibility of nature (this is a further development of the distinction between "water" and other sensibility). Secondly, the infinite is in constant motion, and the infinite develops a stereotyped perceptual object in the movement, so the infinite is not a static and dead thing, but a living thing that is constantly moving.

Anaximenes:

Anaximenes was Anaximander's assistant, and Anaximenes believed that "qi" was the origin of all things. First of all, "Qi" is unique, and the difference between Qi and "infinity" is a process, and Qi is different from other "pseudo-infinite" perceptual objects (such as water). Secondly, "Qi" has intermediary properties. When "Qi" is diluted, it becomes "fire (the most uncertain)", and when condensed, it becomes "wind", "cloud", "water", "earth" and "stone". have eternity.

Unlimited questions:

The question of infinity comes from the inability of the Milesian school to reconcile the relationship between the infinite (amorphous) as the original basis and the finite (fixed). In other words, it is impossible to solve the problem of how the amorphous "one" can derive the fixed "many". This question is discussed in the phase of the three philosophers Pythagoras, Heraclitus and Parmenides.

Pythagoreans:

Pythagoras is different from the school of Pythagoras, who was the founder of the school of Pythagoras. The Pythagorean School is a very scattered religious and political organization, and its schools are independent of each other. The views of the Pythagoreans were codified by Philolaus in the 5th century BC.

"Infinite" and "Finite", "Form" and "Material":

The greatest contribution of Pythagoras is to put forward the form, thus establishing the relationship between "matter" and "form". In pre-Socratic philosophy, "form" does not correspond to "one", and "matter" does not correspond to "many". It presents itself in an opposite form. The "infinity" proposed by Anaximander is the substance, and its counterpart is precisely the "matter" that becomes "one", while the "number" (finite) proposed by the Pythagorean school is beyond the perceptual The reality of which it corresponds is precisely the "form" that becomes "many".

number:

The Pythagoreans' understanding of "number" is based on the understanding of geometry, and "number" was discovered by the Pythagoreans in the study of geometry, in other words, Pythagore The Lars school discovered the relationship (measurement, order, proportion) between form (number) and matter (sensibility), so the properties of numbers also have geometric properties.

Example: The length of a string (a number of geometric properties) determines the tone produced by the vibration of the string.

Therefore, the Pythagoreans also established that "one" constitutes "number" (many), "number" (many) constitutes a point, a point constitutes a line, a line constitutes a surface, a surface constitutes a body, and a body constitutes an element. The theory of creation that transitioned from mathematics to physics. Therefore, the Pythagoreans canceled the original status of the amorphous (infinite), and used the fixed (finite) "number" to explain the amorphous (infinite) sensibility. Therefore, "number" is the measure of all things. But there are also problems with "numbers". The static nature of "numbers" determines that numbers cannot be used to explain motion. This problem will be solved by Heraclitus' transformation of "numbers". Heraclitus would inherit the Pythagorean understanding of the relationship between "numbers" and sensible things to come up with the concept of Logos.

"Odd" and "Even":

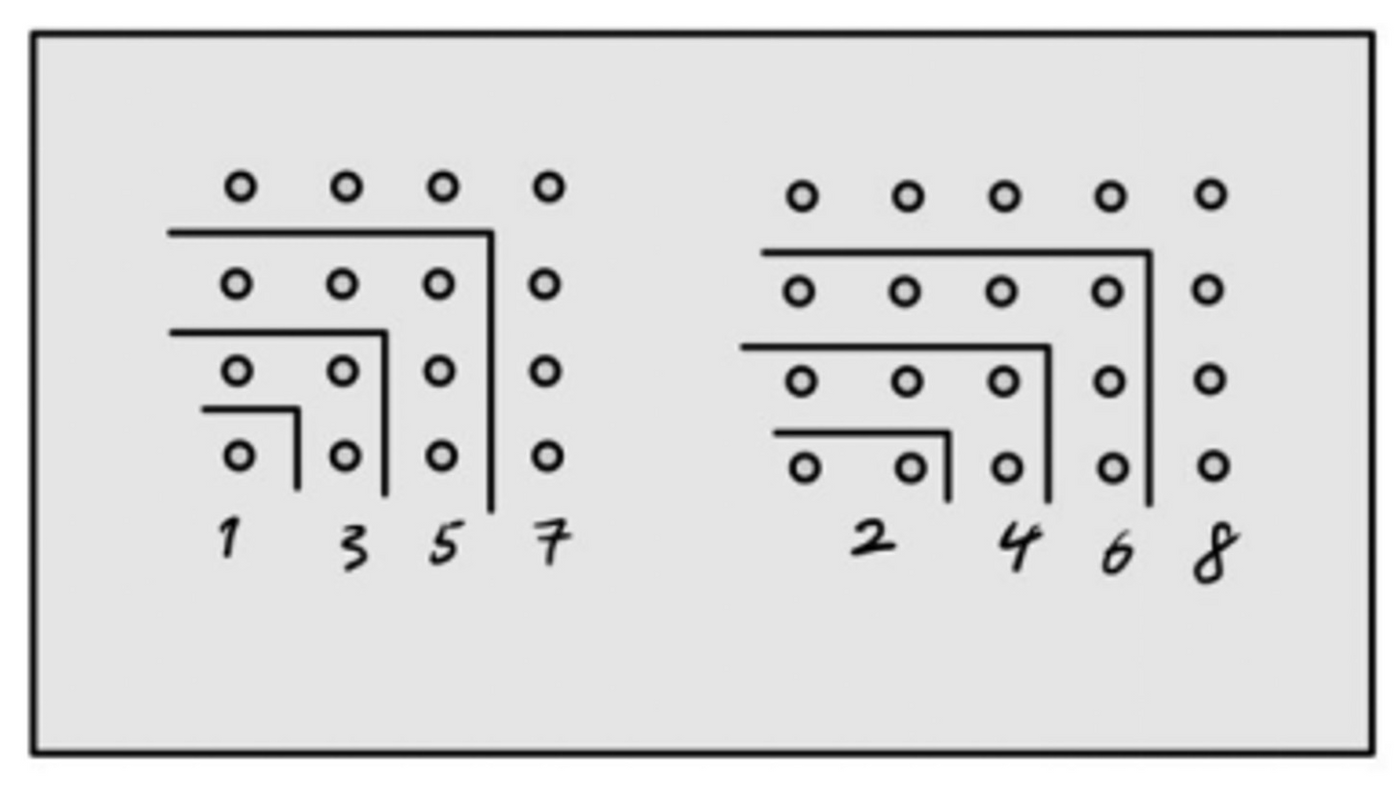
"Odd numbers" are finite (fixed), while "even numbers" are infinite (amorphous). "One" is both "odd" and "even", so one is both "finite" and "infinite". Infinite addition of odd numbers results in square numbers, while infinite addition of even numbers results in rectangular numbers (Figure 1). Because the ratio of "length" to "width" of square numbers is 1:1, square numbers symbolize stability, that is, finiteness (fixed shape). The ratio of "length" and "width" of the holding number is uncertain, so the rectangular number also symbolizes indefiniteness, that is, infinity (amorphous).