進階期權交易：包含 Python 程式碼的綜合指南

8 月 18 日

選擇權交易是一種先進且多功能的交易策略，為交易者提供了在各種市場條件下成長的大量機會。了解高階期權交易的複雜性，包括期權希臘、波動性策略、定價模型和風險管理，對於成功至關重要。在本綜合指南中，我們將深入研究高級期權交易的世界，涵蓋從高級期權交易概述到策略及其實施的複雜性的所有內容。作為了解期權交易基礎知識的交易者，本指南將為您提供有效駕馭複雜的高級期權交易世界所需的技能和見解。

進階期權交易概述

期權（Options）又稱爲選擇權（下文的期權與選擇權都代指Options），它是一種金融衍生工具。當標的資產價格在設定時間段內超過約定的價格時，期權持有方擁有要求賣方按照約定價格買賣資產的權利，但非義務。

高級期權交易業務超越了看漲期權和看跌期權的基本買賣。它涉及期權合約的有用組合以實現特定的交易目標。

現在讓我們來看看高級期權交易所需的概念。

進行高級期權交易時的要點
高級期權交易有一些要點，它們是：

價差：涉及買賣同一標的資產具有不同執行價格或到期日的選擇權合約。透過組合這些合同，您可以建立明確的風險和回報概況。
希臘字母：選擇權希臘字母是代表影響選擇權價格的關鍵因素的字母，包括 Delta、Gamma、Vega、Theta 和 Rho。了解希臘人對於分析和管理選擇權部位至關重要。
波動性：高階策略通常利用波動性預期。有些策略從高波動性中受益，而有些策略則在低波動性環境中獲利。（您可以在本課程中了解有關高級波動率交易的所有內容。）

高級期權交易涉及的策略一些常見的高級期權交易策略是：

多頭跨式選擇權和寬跨式選擇權（Long Straddle and Strangle）：買入到期日相同、行使價不同的買權和賣權。
鐵禿鷹和鐵蝴蝶（Iron Condor and Iron Butterfly:）：結合熊市買權價差和牛市賣權價差。
日曆價差（Calendar Spread）：賣出一份近期選擇權並買入一份具有相同執行價格的長期選擇權。
蝴蝶價差（Butterfly Spread:）：一種有限風險、有限報酬的選擇策略。

此外，了解何時儘早行使（買入/賣出）選擇權以獲取潛在收益或避免不必要的任務對於高階策略至關重要。

接下來，讓我們看看為什麼期權交易對交易者如此有吸引力。

為什麼期權交易有吸引力？

選擇權交易吸引交易者的原因有幾個，以下是上訴的詳細內容：

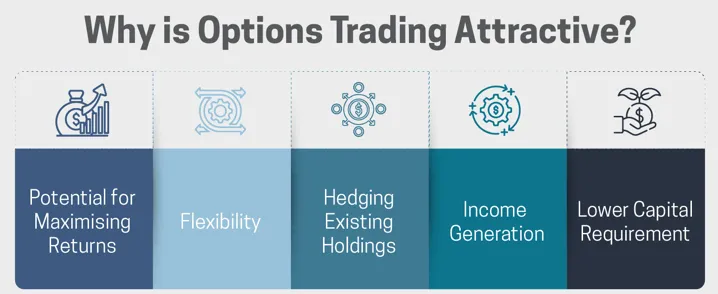
回報最大化的潛力：選擇權提供了放大回報的潛力，特別是對於較小的初始投資。這種槓桿可能很有吸引力，但它也放大了潛在的損失，可以透過適當的風險管理技術來管理。
靈活性：選擇權提供了比單純買賣股票更廣泛的策略。交易者可以在各種市場條件（看漲、看跌、中性或波動）下建立頭寸以增加交易量。與基本股票交易相比，這種靈活性可能帶來更高的回報。
對沖現有持有量：選擇權可用於對沖現有股票頭寸，作為針對價格波動的一種保險形式。透過策略性地購買看跌期權，交易者可以限制其所持股票的潛在損失。
創收：即使標的股票價格保持不變，某些選擇權策略（例如出售備兌買權）也可以產生回報。這對於注重收入的投資者來說很有吸引力。
較低的資本要求：與直接購買股票相比，選擇權通常需要較小的初始投資，從而允許交易者以較少的資本控制相同的標的資產。這對於資金有限的交易者來說可能很有吸引力。

然而，必須承認期權交易也存在一些風險。這些風險包括整個投資的潛在損失、由於時間衰減而導致的價值快速損失以及選擇策略的複雜性，這可能會導致意想不到的結果。因此，交易者徹底了解選擇權交易並採用風險管理策略來保護自己的投資至關重要。

主要期權希臘字母

主要選擇權希臘字母是一組五個字母，代表影響選擇權價格的關鍵因素。這些是選擇權交易者分析和管理其頭寸風險的基本工具。

以下是每個希臘文的意思：

Delta德爾塔 (Δ)

衡量選擇權價格相對於標的資產（股票、債券等）價格 1 美元變化的變化率。
買權的 Delta 通常在 0 到 1 之間，表示其變動方向與標的資產相同，但幅度較小。
看跌期權的 Delta 通常介於 -1 和 0 之間，表明它將朝著與標的資產相反的方向移動。

Gamma伽瑪 (γ)

代表Delta的變化率。它告訴您隨著標的資產價格的變動，Delta 本身會發生多少變化。
正的 Gamma 表明 Delta 正在增加，這意味著選擇權的價格將對標的資產價格的變化變得更加敏感。
負 Gamma 表示 Delta 正在減少，這意味著選擇權的價格對標的資產價格變化的敏感度將降低。

Theta西塔 (θ)

衡量由於時間的推移而導致的期權價格衰減率，也稱為時間衰減。
在其他條件相同的情況下，選擇權越接近到期，其價格就越低（Theta 為負值）。
Theta 對於短期選擇權策略尤其重要，因為時間衰減會迅速侵蝕利潤。

Vega織女星 (ν)

衡量選擇權價格對隱含波動率變化的敏感度。
隱含波動率反映了市場對標的資產未來價格波動的預期。
高 Vega 表示選擇權的價格對隱含波動率的變化較為敏感。相反，Vega 較低則表示價格受到的影響較小。

Rho羅 (ρ)

衡量選擇權價格對利率變化的敏感度。
一般來說，較高的利率會導致選擇權價格略低，反之亦然。然而，與其他希臘人相比，Rho 的影響通常較小。

接下來，我們將詳細討論選擇權希臘人對選擇權定價的影響。

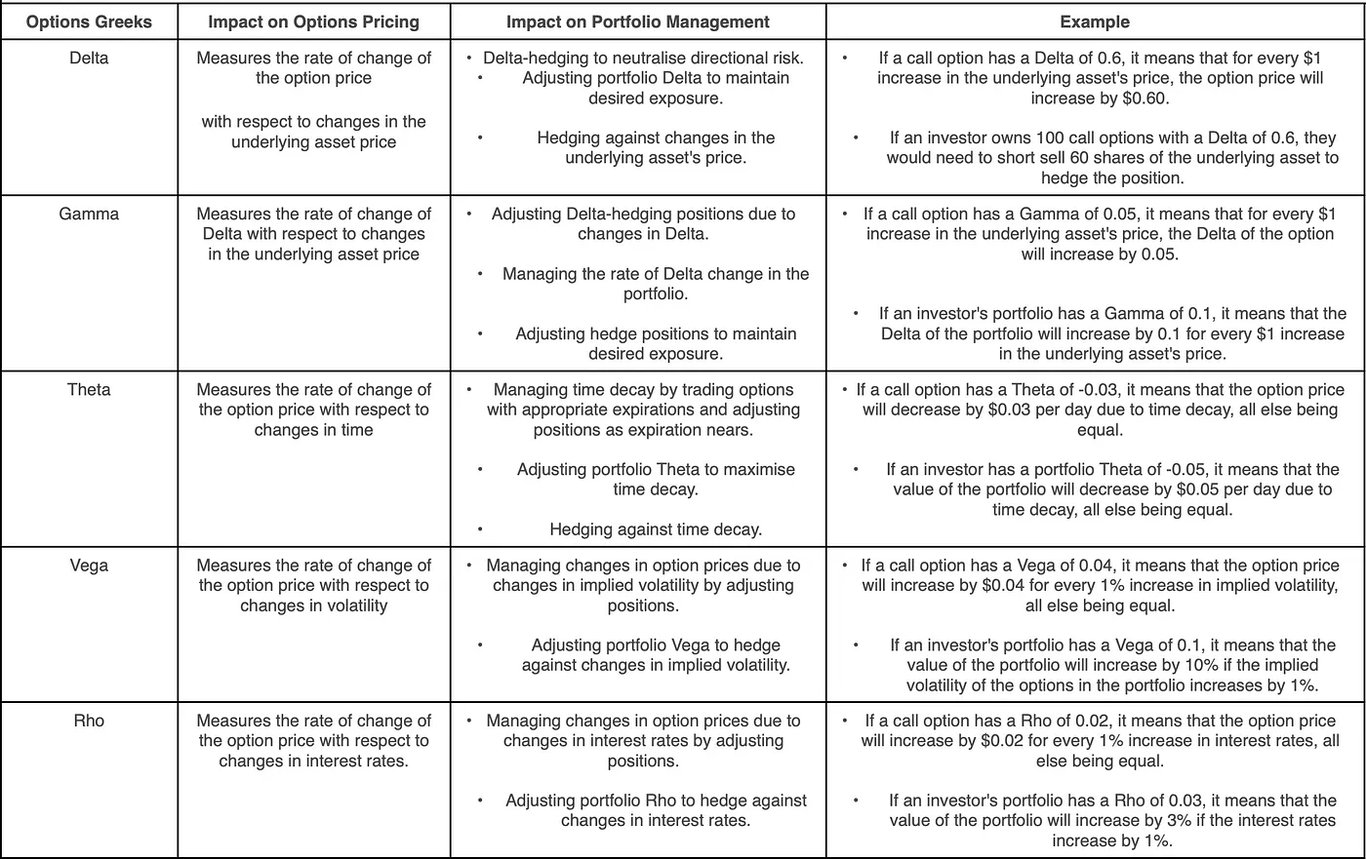
期權希臘字母對選擇權定價與投資組合管理的影響

在這裡，我們將再次看到主要的期權希臘人，但將討論每個希臘人對期權定價和投資組合管理的影響，並提供每個例子。選擇權希臘人對選擇權價格對各種市場因素變化的反應以及投資組合管理都有特定的影響。

現在我們將了解實施高階選擇權交易策略所需的技能。

實施高階期權交易策略的技能

以下是您需要培養的一些基本技能，以便透過高級期權交易策略取得成功：

技術知識

深入了解選擇權希臘人：掌握 Delta、Gamma、Theta、Vega 和 Rho 至關重要。您應該能夠解釋它們對選擇權定價和投資組合行為的影響。
波動率分析：能夠評估歷史波動率和隱含波動率以及影響波動率的因素，對於制定基於波動率的策略至關重要。
高階選擇權定價模型：雖然基本的 Black-Scholes 模型可能足以滿足某些策略的需要，但了解 Heston 或 SABR 等更複雜的模型可以更深入地了解選擇權定價動態，尤其是在波動的市場中。
風險管理技術：進階策略通常涉及管理多條腿（買入/賣出不同的選擇權）。 Delta 對沖和利差調整等技術對於降低風險至關重要。
投資組合建構：能夠結合不同的選擇權策略來實現特定的風險回報狀況並對現有資產進行對沖是一項寶貴的技能。

分析能力

市場分析：高階策略通常依賴特定的市場前景或波動性預期。需要強大的分析能力來解釋市場數據和技術指標，以做出明智的決策。
回測策略：使用歷史資料測試策略的能力（回測）有助於評估其潛在表現並在拿實際資本冒險之前識別弱點。
情境分析：考慮您的部位對不同市場情境（上漲/下跌、波動性變化）的反應對於風險管理至關重要。

交易技巧

紀律與耐心：高階策略通常需要等待特定市場條件的出現。紀律和耐心對於避免偏離計畫的衝動交易至關重要。
訂單管理：了解不同的訂單類型（市價訂單、限價訂單、止損訂單）以及如何有效使用它們對於管理部位的進場和出場至關重要。
情緒控制：選擇權交易的快節奏和潛在的波動性可能會引發情緒反應。保持情緒控制並堅持您的交易計劃對於成功至關重要。

額外技能

編碼技能：在當今技術驅動的交易領域，基本編碼知識 (Python) 有助於回測策略、自動化計算或使用高級期權定價模型。
研究技能：隨時了解選擇權交易策略、市場趨勢和相關財經新聞的新發展對於持續學習和適應非常重要。

現在讓我們看看看跌期權平價意味著什麼以及更多相關內容。

Python 中的看漲期權平價是什麼？

賣權平價（PCP）是歐式買權、歐式賣權、標的資產價格、無風險利率與到期時間的關係。它本質上規定，根據執行價格的現值調整的看漲期權的價格應等於看跌期權的價格加上當前股票價格。

以下是一個 Python 程式碼，用於計算看跌期權奇偶校驗並評估其對於給定參數集的有效性：

S：目前股價
K：執行價格
C：買權價格
P：賣權價格
r：無風險利率（年化）
T：到期時間（以年為單位）

它使用以下公式計算看跌期權平價：

C — e^(-rT) * K = P + S

然後，函數顯示方程式的左側 (LHS) 和右側 (RHS)，以及它們之間的差異。它還檢查差異是否接近零，表明看跌期權平價大致成立。

這是 Python 程式碼：

import math

def calculate_put_call_parity(S, K, C, P, r, T):

  # Left-hand side (LHS) of Put-Call Parity
  lhs = C - math.exp(-r * T) * K

  # Right-hand side (RHS) of Put-Call Parity
  rhs = P + S

  # Difference between LHS and RHS
  parity_difference = lhs - rhs

  print("Put-Call Parity Calculation:")
  print(f"Left-hand side (LHS): Call option price adjusted for present value of strike - {lhs}")
  print(f"Right-hand side (RHS): Put option price + Stock price - {rhs}")
  print(f"Difference between LHS and RHS: {parity_difference}")

  # Check if Put-Call Parity approximately holds (small difference due to rounding)
  if abs(parity_difference) < 1e-5:
    print("Put-Call Parity approximately holds.")
  else:
    print("Put-Call Parity does not hold.")

  return parity_difference

# Example usage:
S = 100  # Stock price
K = 110  # Strike price
C = 5    # Call option price
P = 7    # Put option price
r = 0.05  # Risk-free interest rate (5%)
T = 1    # Time to expiration (in years)

parity_difference = calculate_put_call_parity(S, K, C, P, r, T)

Output:

Put-Call Parity Calculation:
Left-hand side (LHS): Call option price adjusted for present value of strike - -99.63523669507855
Right-hand side (RHS): Put option price + Stock price - 107
Difference between LHS and RHS: -206.63523669507856
Put-Call Parity does not hold.

接近零的值表示奇偶校驗成立，但在上面的輸出中，它表明看跌期權奇偶校驗不成立。

接下來讓我們轉向期權定價。

期權定價

選擇權定價涉及確定選擇權合約的公允價值，這賦予持有人以以下價格購買（如果是看漲選擇權）或出售（如果是看跌選擇權）標的資產的權利，但沒有義務。價格）。

下面您將看到兩種類型的選擇權定價技術以及它們之間的差異。這些類型是：

選擇權的內在價值
選擇權的時間價值

選擇權的內在價值

選擇權的內在價值是指選擇權立即行使時所具有的價值。

下面您可以看到它們是如何計算的。


Intrinsic Value of Call Option = Current Market Price of Underlying Asset - Strike Price
Intrinsic Value of Put Option = Strike Price - Current Market Price of Underlying Asset

選擇權的時間價值

選擇權的時間價值是指選擇權買方為在到期前擁有選擇權的特權而支付的權利金。它反映了期權在到期時最終成為價內期權的機率。

Time Value = Option Premium - Intrinsic Value

展望未來，我們將了解選擇權定價模型。

期權定價模型

選擇權定價模型是用來決定選擇權公允價值的數學模型。您將在下面找到不同的期權定價模型以及每個模型之間的主要差異。

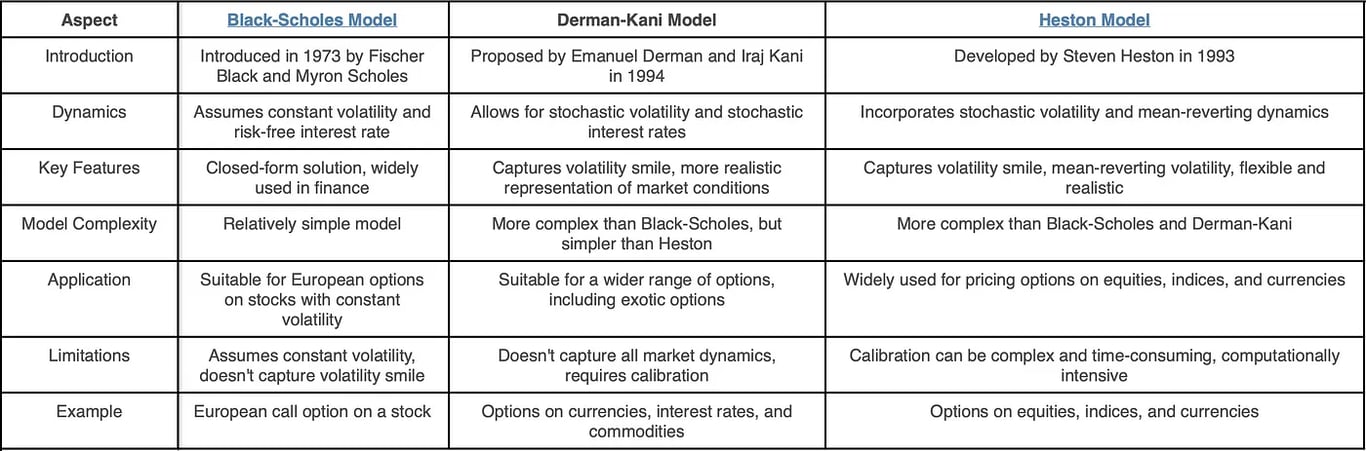
每種模型都有其優點和局限性，模型的選擇取決於交易者或投資者的特定要求。

現在讓我們來看看最受歡迎的高階選擇策略之一，即蝴蝶策略及其收益圖。

使用 Python 的蝴蝶期權交易策略範例

要獲得蝴蝶策略的收益圖，您需要遵循以下步驟：

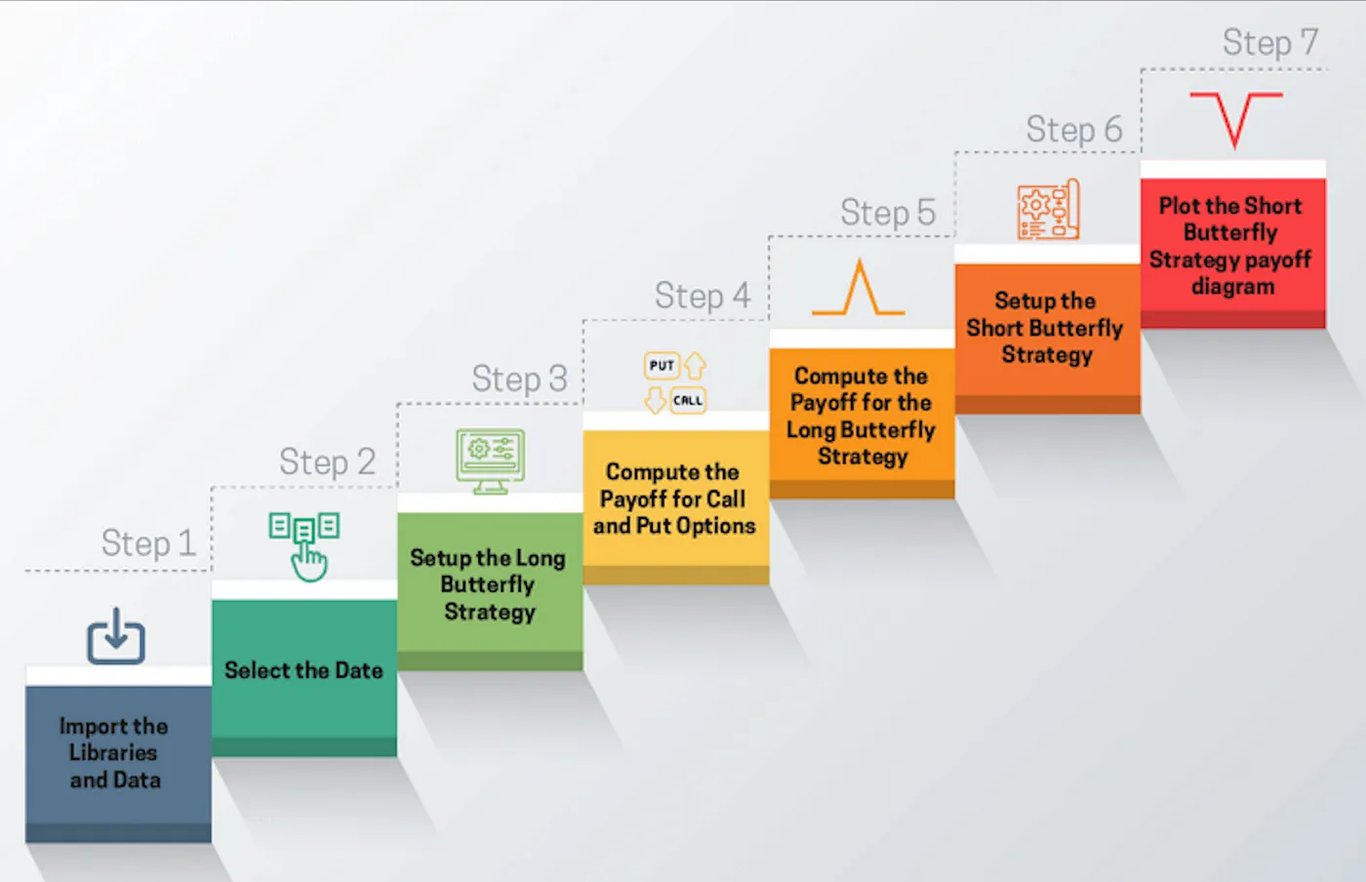
建立策略並了解您將使用什麼類型的選項。
了解每個選擇權將使用哪個執行價格。
選擇一個價格範圍，您將與該價格範圍比較每個選擇權的收益。
將策略效益計算為蝴蝶策略中使用的所有選項的收益總和。
根據價格範圍繪製策略收益。

學習此策略後，您將能夠繪製您可能想要設定的任何選擇權策略的收益圖。

步驟如下：

# For data manipulation
import pandas as pd
import numpy as np

# For data visualisation
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('seaborn-darkgrid')

# For option's payoff computations
import sys
sys.path.append('..')
from data_modules.options_util_quantra import setup_butterfly


# Read the options data
options_data = pd.read_pickle('../data_modules/nifty_options_data_2019_2022.bz2')

# Read the futures data
futures_spot_data = pd.read_pickle(
    '../data_modules/nifty_data_2019_2022.bz2')[['futures_close', 'Expiry']]

# Print the last 5 rows of the futures data
futures_spot_data.tail()

輸出：

futures_close ExpiryDate 2022-05-20 16253.25 2022-05-262022-05-23 16183.35 2022-05-262022-05-24 16104.70 2022-05-262022-05-25 16013.80 2022-05-262022-05-26 16159.05 2022-05-26

第 2 步：選擇日期

# Set the analysis dateanalysis_date = "2021-01-01"# Fetch the futures close price that corresponds to the above datefutures_price = futures_spot_data.loc[analysis_date, 'futures_close']# Fetch the options chain data that belongs to the above dateoptions_chain = options_data.loc[analysis_date]# Print the futures close price of the datef"The futures price on {analysis_date} is {futures_price}"

Output:


'The futures price on 2021-01-01 is 14053.85'

# Print the options chain data of the above date
options_chain.head()

Symbol Expiry Option Type Strike Price Open High Low Close Last Settle Price Number of Contracts Turnover Premium Turnover Open Interest Change in OI Underlying
Date                                
2021-01-01 NIFTY 28-01-2021 CE 12000 2017.10 2062.25 2014.0 2043.60 2042.00 2043.60 256.0 269606000.0 39206000.0 456225.0 10200.0 14018.5
2021-01-01 NIFTY 28-01-2021 CE 12050 0.00 0.00 0.0 609.75 0.00 2009.45 0.0 0.0 0.0 0.0 0.0 14018.5
2021-01-01 NIFTY 28-01-2021 CE 12100 1923.15 1936.45 1922.6 1934.75 1934.75 1960.25 4.0 4209000.0 579000.0 15750.0 0.0 14018.5
2021-01-01 NIFTY 28-01-2021 CE 12150 0.00 0.00 0.0 569.95 0.00 1911.10 0.0 0.0 0.0 0.0 0.0 14018.5
2021-01-01 NIFTY 28-01-2021 CE 12200 0.00 0.00 0.0 1797.80 1799.00 1862.15 0.0 0.0 0.0 22575.0 0.0 14018.5

步驟三：制定多頭蝴蝶策略

# Setup the butterfly strategybutterfly = setup_butterfly(futures_price, options_chain, "long")# Print the strategy dataframebutterfly

Output:

Option Type Strike Price position premium0 CE 14050 -1 280.751 PE 14050 -1 279.002 CE 14600 1 69.253 PE 13500 1 103.00

步驟四：計算買權和賣權的收益

既然我們已經建立了多頭蝴蝶策略，現在讓我們計算買權和賣權的收益。請記住，多頭買權的收益由下式給出：

Long Call Payoff=𝑀𝑎𝑥(Spot Price−Strike Price,0)−Premium

Max 函數解釋如下：

如果現貨價格高於執行價格，則多頭買權收益為現貨價格與執行價格之間的差額。
如果現貨價格低於執行價格，則多頭買權收益為 0。

你能猜出如何計算空頭買權嗎？很簡單，您只需將上述函數乘以 -1 即可獲得賣空版本的看漲期權收益。

定義呼叫支付函數

# Setup the butterfly strategy
butterfly = setup_butterfly(futures_price, options_chain, "long")

# Print the strategy dataframe
butterfly

Output:

  Option Type Strike Price position premium
0 CE 14050 -1 280.75
1 PE 14050 -1 279.00
2 CE 14600 1 69.25
3 PE 13500 1 103.00

第 5 步：計算多頭蝴蝶策略的效益

# Compute long call payoff value
call_payoff_value = call_payoff(16000, 15000, 20, 1)

# Print the long call payoff value
call_payoff_value

Output:

# Compute the short call payoff value
call_payoff_value = call_payoff(16000, 15000, 20, -1)

# Print the short call payoff value
call_payoff_value

Output:

- 980

然後，類似地，我們可以定義看跌期權收益。

對於多頭看跌期權收益，我們有以下公式及其解釋：

多頭賣權收益 = 𝑀𝑎𝑥(行使價−現貨價格,0)−權利金

如果執行價格高於現貨價格，則多頭賣權收益為執行價格與現貨價格之間的差額。
如果執行價格低於現貨價格，則多頭賣權收益為 0。

# Define the put payoff function
def put_payoff(spot_price, strike_price, premium_spent, position):
    return (np.maximum(strike_price - spot_price, 0) - premium_spent) * position
    
# Compute the long put payoff value
put_payoff_value = put_payoff(16000, 15000, 20, 1)

# Print the long put payoff values
put_payoff_value

Output:

-20

最後，空頭賣權收益值：

# 計算空頭看跌期權收益值
put_payoff_value = put_payoff(16000, 15000, 20, -1) 

# 列印空頭看跌期權收益值
put_payoff_value

輸出：

第 6 步：制定空頭蝴蝶策略

def get_payoff(spot_price_expiry, options_strategy):

    # Create a payoff column with empty values
    options_strategy['payoff'] = np.nan

    # Create a loop to go through each option that belongs to the butterfly strategy
    for i in options_strategy.index:

        # Check if the option is a call
        if options_strategy.loc[i, 'Option Type'] == 'CE':

            # Compute the call payoff as per its corresponding values
            options_strategy.loc[i, 'payoff'] = call_payoff(
                spot_price_expiry, options_strategy.loc[i, 'Strike Price'], options_strategy.loc[i, 'premium'], options_strategy.loc[i, 'position'])

        # Check if the option is a put
        elif options_strategy.loc[i, 'Option Type'] == 'PE':

            # Compute the put payoff as per its corresponding values
            options_strategy.loc[i, 'payoff'] = put_payoff(
                spot_price_expiry, options_strategy.loc[i, 'Strike Price'], options_strategy.loc[i, 'premium'], options_strategy.loc[i, 'position'])

    # Return the payoff sum of the 4 options
    return options_strategy['payoff'].sum()

讓我們舉個例子。讓我們針對特定價格呼叫 get_payoff 函數，看看到期時的價值是多少。

get_payoff(13100, butterfly)

Output:

-162.5

# Create the payoff dataframe
payoff = pd.DataFrame()

# Compute the price range
payoff['price_range'] = options_chain['Strike Price'].unique()

# Print the last 5 rows of the price range of the payoff dataframe
payoff['price_range'].tail()

Output:

66    15300
67    15350
68    15400
69    15450
70    15500
Name: price_range, dtype: int64

# Compute the butterfly strategy payoff values
payoff['pnl'] = payoff.apply(
    lambda r: get_payoff(r.price_range, butterfly), axis=1)

# Print the last 5 rows of the strategy payoffs
payoff['pnl'].tail()

Output:

66   -162.5
67   -162.5
68   -162.5
69   -162.5
70   -162.5
Name: pnl, dtype: float64

# Set price_range as index
payoff.set_index('price_range', inplace=True)

# Set figure size
plt.figure(figsize=(15, 7))

# Plot the payoff data
plt.plot(payoff)

# Set the title and labels and their sizes
plt.title('Long Butterfly Strategy Payoff Diagram', fontsize=16)
plt.xlabel('Price (Rupees)', fontsize=15)
plt.ylabel('Payoff (Rupees)', fontsize=15)
plt.tick_params(axis='both', labelsize=15)

# Show the graph
plt.show()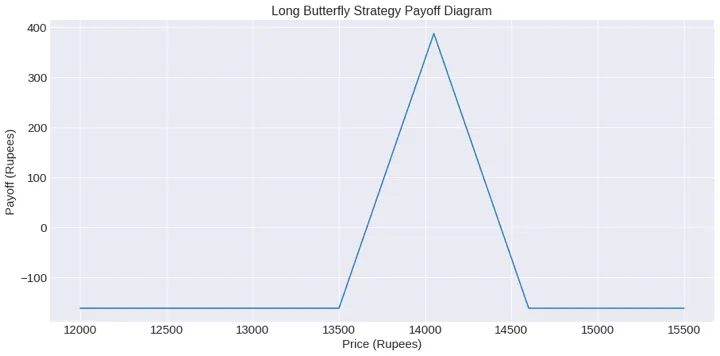

# Print the maximum expected profit for the strategy
max_profit = round(payoff.max(),2)[0]

# Print the futures price corresponding to the maximum profit
max_profit_futures_price = payoff.idxmax()[0]

f"The maximum profit is {max_profit} and its corresponding futures price is {max_profit_futures_price}"

Output:

'The maximum profit is 387.5 and its corresponding futures price is 14050'

因此，如果到期時的期貨價格為 14050，則該策略的最大利潤預計為 387.5 盧比。

# Print the maximum expected loss for the strategy
max_loss = round(payoff.min(),2)[0]

# Print the futures price corresponding to the maximum loss
max_loss_futures_price = payoff.idxmin()[0]

f"The maximum loss is {max_loss}"

Output:

'The maximum loss is -162.5'

第 7 步：繪製空頭蝴蝶策略收益圖

# Setup the butterfly strategy dataframe
butterfly = setup_butterfly(futures_price, options_chain, "short")

# Print the short butterfly dataframe
butterfly

輸出：

 Option Type Strike Price position premium
0 CE 14050 1 280.75
1 PE 14050 1 279.00
2 CE 14600 -1 69.25
3 PE 13500 -1 103.00

# Create the payoff dataframe
payoff = pd.DataFrame()

# Create the price range based on the strike prices of the options chain
payoff['price_range'] = list(options_chain['Strike Price'].unique())

# Compute the payoff values for the short butterfly strategy
payoff['pnl'] = payoff.apply(
    lambda r: get_payoff(r.price_range, butterfly), axis=1)

# Set price_range as index
payoff.set_index('price_range', inplace=True)

# Set figure size
plt.figure(figsize=(15, 7))

# Plot the payoff data
plt.plot(payoff)

# Set the title and labels and their sizes
plt.title('Short Butterfly Strategy Payoff Diagram', fontsize=16)
plt.xlabel('Price (Rupees)', fontsize=15)
plt.ylabel('Payoff (Rupees)', fontsize=15)
plt.tick_params(axis='both', labelsize=15)

# Show the graph
plt.show()

Output:

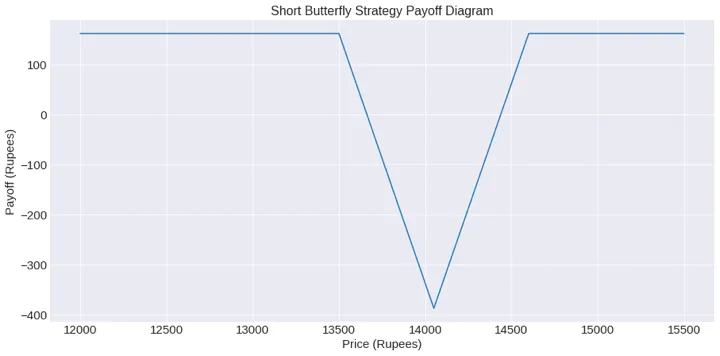
正如您所看到的，收益圖讓我們直觀地了解何時可以透過多頭或空頭蝴蝶策略獲得最大回報。上面的程式碼可用於您想要獲得的任何策略效益。

您可以透過系統選擇權交易課程查看整個策略以及更多有關蝴蝶策略的資訊。本課程也將幫助您詳細學習回測期權交易策略和相關概念。

值得注意的是，回測結果並不能保證未來的表現。所提供的策略結果僅用於教育目的，不應被解釋為投資建議。有必要對多個參數的策略進行全面評估，以評估其有效性。

現在，我們將了解如何在高級選擇權交易中進行風險管理。

進階期權交易中的風險管理

風險管理對於高級期權交易至關重要，可以保護您的資本並優化您的回報。

以下是高階選擇權交易的一些關鍵風險管理策略：

頭寸規模：確定您願意在任何單筆交易中承擔風險的最大資本金額。這可以確保您不會過度暴露於任何一種職位。
多元化：透過不同標的資產、產業和策略的選擇權交易多元化來分散風險。
止損訂單：使用停損訂單來限制選擇權部位的潛在損失。根據您的風險承受能力和標的資產的波動性設定停損水準。
對沖：使用買入保護性看跌期權或賣出有擔保看漲期權等策略對沖您的期權頭寸，以抵消潛在損失。
波動性管理：了解波動性對選擇權價格的影響並相應調整您的部位。考慮使用從波動性變化中受益的策略，例如跨式選擇權或寬跨式選擇權。
風險報酬率：在選擇權交易中保持有利的風險報酬率。目標是潛在回報遠遠超過潛在風險的交易。
定期監控：定期監控您的選擇權頭寸，並準備好在市場狀況發生變化或您的交易理論不再成立時調整或平倉。
風險分析工具：在進行選擇權交易之前，使用經紀商或第三方軟體提供的風險分析工具來評估選擇權交易的潛在風險和回報。
部位調整：制定計畫來調整或平倉未如預期執行的選擇權部位。這可能涉及將頭寸展期、調整執行價格或平倉虧損頭寸以限制損失。
持續學習：隨時了解市場趨勢、經濟指標等可能影響選擇權價格的因素。不斷學習先進的選擇權交易策略和風險管理技術。

透過實施這些風險管理策略，您可以最大限度地降低下行風險，同時最大限度地提高高級選擇權交易的潛在回報。

最後但並非最不重要的一點是，我們將看到可用於學習選擇權交易的資源。

有關高級期權交易的常見問題

以下是選擇權交易者通常會問的問題。因此，我們已經為前面的每個問題提供了答案。

Q：進階交易中影響選擇權定價的主要因素有哪些？
答：高級交易中的選擇權定價受以下幾個因素影響：

標的資產價格：標的資產的當前價格顯著影響選擇權的價值。
執行價格：執行價格與標的資產當前價格之間的關係會影響選擇權的內在價值。
到期時間：選擇權到期之前的剩餘時間會影響其時間價值。
波動性：隱含波動性衡量市場對未來波動性的預期，對選擇權定價有重大影響。
利率：利率的變動會影響選擇權現金流的現值。
股利：對於股票選擇權，股利支付的時間和規模會影響選擇權定價。

Q：如何選擇合適的選擇權合約進行進階交易？
答：選擇正確的選擇權合約需要考慮以下幾個因素：

標的資產：根據您熟悉並深入分析的標的資產選擇選擇權合約。
市場狀況：考慮當前的市場狀況，包括波動性、趨勢和流動性。
交易目標：確定您的交易目標，無論您是在尋求創造收入、投機還是對沖。
風險承受能力：評估您的風險承受能力並選擇符合您的風險管理策略的選擇權合約。
選擇權希臘人：分析選擇權希臘人以了解選擇權價格對各種因素變化的敏感度。
到期日：選擇與您的交易時間表和對標的資產的預期相符的到期日。

Q：隱含波動率在高階選擇權交易中發揮什麼作用？
答：隱含波動率是選擇權定價和高階選擇權交易的關鍵因素：

選擇權定價：隱含波動率反映了市場對未來波動率的預期，是選擇權定價模型的關鍵輸入。
策略選擇：高隱含波動率可能導致選擇權定價過高，使賣出選擇權等策略更具吸引力，而低隱含波動率可能有利於買入選擇權。
風險管理：隱含波動率可以幫助交易者評估其選擇權部位的潛在風險並相應調整策略。
市場情緒：隱含波動率的變化可以顯示市場情緒的變化，並提供對未來價格趨勢的洞察。

Q：在進階期權交易中需要避免哪些常見錯誤？
答：在進階期權交易中要避免的常見錯誤包括：

過度槓桿：相對於帳戶規模而言，持倉量過大進行交易。
忽略風險管理：未能使用停損單或風險管理技術來限制損失。
忽略隱含波動率：選擇選擇權策略時不考慮隱含波動率。
缺乏多元化：交易集中在單一標的資產或策略，增加了投資組合風險。
追逐回報：只專注於潛在利潤而不考慮潛在風險。
未能規劃：沒有明確的交易計畫或策略進行交易。
忽視市場狀況：未能根據當前市場狀況調整交易策略。

Q：我如何及時了解與高階選擇權交易相關的市場動態？
答：您可以透過以下方式了解市場動態：

市場研究：定期查看財經新聞、市場分析和經濟報告，隨時了解可能影響選擇權價格的動態。
技術分析：監控技術指標和圖表模式以識別潛在的交易機會。
選擇權教育：不斷自我教育高階選擇權交易策略與風險管理技術。
專業分析：專注於市場分析師、交易員和金融專家，他們提供與選擇權交易相關的見解和分析。
線上社群：加入線上論壇、交易社群和社群媒體群組，討論交易想法並隨時了解市場趨勢。
經紀商工具：利用經紀商提供的研究工具和資源，例如市場掃描器、選擇權篩選器和研究報告。

Q：我可以在不同的市場條件下使用高階選擇權交易策略嗎？
答：是的，高階選擇權交易策略可以在各種市場條件下使用：

看漲市場：買權多頭、賣權空頭、買權價差和備兌買權等策略可用於看漲市場，從價格上漲中獲利。
看跌市場：看跌市場中可以使用多頭看跌期權、空頭看漲期權、看跌期權價差和看漲期權價差等策略，從價格下跌中獲利。
橫盤市場：鐵禿鷹、蝴蝶和日曆價差等策略可用於橫盤市場，從區間價格波動中獲利。
高波動性市場：跨式選擇權、寬跨式選擇權和比率價差等策略可用於高波動性市場，從大幅價格變動或隱含波動性變動中獲利。
結論
高級期權交易為尋求有效管理風險的投資者提供了大量的策略和工具。了解選擇權希臘字母，即 Delta、Gamma、Vega 和 Theta 至關重要，因為它們直接影響選擇權定價和投資組合管理。
波動性策略對於高階選擇權交易的成功至關重要，掌握實施這些策略所需的技能是關鍵。
了解期權如何定價、影響定價的因素以及各種期權定價模型是基礎。風險管理至關重要，學習如何有效分析選擇希臘人並避免常見錯誤對於成功至關重要。隨時了解市場發展並利用可用資源（例如高級期權交易課程和書籍）對於持續學習和改進至關重要。
透過遵循正確的方法並利用正確的經紀商，交易者可以充滿信心和能力地駕馭高級選擇權交易的世界。
要了解有關高級期權交易的更多信息，我們的期貨和期權市場量化交易學習路線涵蓋了 7 門課程，以開始在期貨和期權交易中使用量化技術。透過這些課程，您將學習波動率預測、期權回測、風險管理、期權定價模型、希臘語以及各種策略，如跨式策略、蝴蝶策略、鐵禿鷹策略、價差策略、離散交易、情緒交易、盒子策略、多元化期貨交易策略還有更多。