CAPM與手扶梯

大家聽過CAPM嗎? 回憶自己跌跌撞撞的經歷,CAPM是我投資知識的分水嶺。相似的,人類在思考「市場」和Markowitz效率前緣的關係之後,又基於既有理論,往前跨了一大步。
1. 我們看過Markowitz以及效率前緣的畫法。以股票為例,每當我加入一家公司,就能把效率前緣又往前擠一些。換句話說,當我採取多資產組合時,可以吃到「免費的午餐」。而當資產分散到極致時,我們的組合表現就會等於市場,這也是「指數投資」的精神。
不過,即使我採取市場組合,還是需要承擔波動風險。也就是說,透過分散投資的方式,我們可以把風險壓到極限,但這極限又是什麼呢? 答案就是「不可分散風險」,或是「系統性風險」,代號β (beta)。相對的,那些可分散風險,也被稱為「非系統性風險」,代號α (alpha)
在市場上,我們必須透過冒險,才有可能取得預期報酬,但不代表只要冒險就一定有收穫。
賽車的雨天進站策略,就是一種賭注,因為雨胎適合溼地,但在乾地上反而不理想。所以如果天氣發展不如車隊預期,選擇換胎反而會讓圈速下滑。(各位可以試著雨天跑kart,感受胎溫過低的刺激。) 不過,無論車隊如何選擇,都是「不可避免」的冒險,因為他們的目標是取得最佳成績。一個錯誤的押注方向,往往已經是當時最好的策略。那什麼是「可避免」的冒險呢? 例如搶桿位的時候,故意把車開出賽道,風險十足,但是不會讓圈速上升。因此,聰明的車隊,應該要承受必要的風險,而遠離非必要風險,這道理在市場上也適用。聰明的投資者,應該清楚自己承受的風險,而不是盲目冒險。
2. 我很喜歡在手扶梯上往回跑,只要速度適中,我可以連續跑幾分鐘都留在相似位置。想像一下,如果現在有一堆人跟我一樣開始跑步,只是方向和速度都不同,大家要如何分出高下? 你可能會有兩種方案,第一種是乾脆停掉電梯,第二種是站在一旁觀測,並扣掉電梯的速度影響。在市場上,如果我們從宏觀的視角檢視,會發現每個標的都像在手扶梯上跑步。或者從個體的角度,一項資產會受到自身能力和整體環境的綜合影響,對應的價格也會產生波動。
回到主題,簡單來說,從均值-方差模型來看,觀測者會認為公司股票的預期收益來自於價格波動。可是波動風險又可以拆成 α + β ,我們應該使用更精細的衡量標準。因此,Sharpe等人在Markowitz奠定的基礎上,提出了「資本資產定價模型」(capital asset pricing model, CAPM),用「市場風險β」來解釋單一資產的獲利來源。
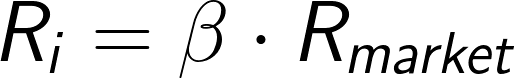
β: 隨著市場波動的敏感度
在真實世界中,我們需要另外考慮「無風險資產」,有些人會使用短期國債的利率來代替,因此我們把公式微調。
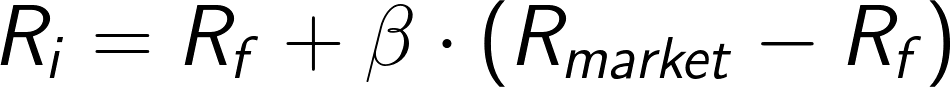
3. 用CAPM來描述資產價格有什麼好處呢?
顯而易見,由於使用了「市場風險」,我們只需要把β和R「線性結合」即可。舉個簡單的例子,如果無風險利率是1%,長榮的β是3,此時大盤漲10%,那長榮的預期回報就是 1%+3×(10%-1%)=28%. (數字隨便猜的,本人沒有相關股票。) 由於大家都知道大盤的漲跌和無風險利率,因此投資者只要計算出手中股票的β,就能快速得出合理的預期收益。
如果我們認同「回報來自於波動」,那麼CAPM可以很簡潔的描述兩者的關係。當投資者願意承受高度波動時,往往可以得到相應的高回報,而應用CAPM的語言,就是他採取高β策略。從這個角度來看,一支飆股不會比穩定股更好,畢竟高回報的背後是高風險,往上飆的股票很可能也會往下衝。換句話說,我們可以用簡單的波動風險,來描述手中的持股,而想要多大的β,就見仁見智了。
4. 奇怪,α躲到哪裡了?
不是我故意提到α卻草率帶過,而是CAPM天生就「討厭」α。當我們用「市場風險」來衡量一支股票的收益時,其實已經假設「報酬只和風險有關」,同時也很大程度的相信「市場有效」,也就是天上不會掉禮物。因此,如果大家都是理性投資者,就應該只會想要承受必要風險β,而不會打α的主意。
問題是,當我們回頭檢視手中資產時,會發現CAPM無法只靠β完美解釋真正價格,而對於這些差異,有些人會用α來表達。簡單來說,β之外的報酬,我們可以通稱為α,因此也有人稱α為「超額報酬」。(超額報酬有很多種意思,這是其中一種。) 事實上,當我們使用CAPM的精神來衡量基金經理人時,也會得到β和「Jensen's alpha」。
5. 現在,讀者朋友可以休息一下,我們來聊些輕鬆的,保證不會有數學公式。
為什麼我要在資產配置系列中提到CAPM呢? 最主要的原因是均值-方差(MV)模型和CAPM有關,而且都認為報酬只來自波動風險。借用指數投資者的名言,任何想要打敗大盤(市場組合)的努力,都是徒勞。或許一支股票或一個經理,能夠短暫戰勝大盤,但是時間拉長來看,這些非系統風險和報酬會彼此抵消。
我知道有些「指數投資者」會有經典理論(尤其是諾貝爾獎)撐腰的傲氣,我也是,OK。
看著一堆人,明明承認報酬來自於波動風險,卻又矛盾的想要打敗系統性報酬,就覺得可笑。就像遇到不會騎車的人,完全不知道怎麼按煞車和轉油門,還想上場比賽,我會很樂意上前揶揄他。減速就是收油,懂嗎? 指數投資最有效率,好嗎?
懂,道理很多人都懂。但是,如果有人說減速要補油,妳又怎麼看? (減速退檔補油可以避免後輪鎖死。) 如果妳選擇先笑再說,那麼有很大的機率,妳是對的,可是很可能也止步於此了。在我看來,有些指數投資人,完全是指數派的信徒而已,很可能受到媒體或師父影響而直接相信。雖然我認為這種信仰很安全,但是不求甚解、不願質疑的心態,很危險。
「狂徒,你是不是想背叛指數投資教派?」看到這裡,我猜會有讀者和作者感到困惑。不過如果你真的讀過我的歷來文章,就會發現,貫穿我所有知識體系的,是「質疑」而不是「信仰」。為了避免誤會,我再強調一次,我非常推崇指數投資,我也認為散戶就該如此。但是,我還是喜歡挑戰所有權威。因此,我依然持續吸收不同理論,化為自己的知識。
自認能打敗大盤的投資者,通常是過度自信,倒不如採用指數投資。不過,如果妳認為自己的策略或持股,能穩定產生α,或是想要彌補β過低的缺點,我會在之後的文章中提到相應手段。(篇名暫定為「加法和乘法」、「還我兩顆地球」。)
6. 接下來我要從理論層面,寫出CAPM的缺點。
首先,只用波動來解釋預期報酬,很有可能是錯的。最簡單的方式就是把模型預測結果和實際價格相比,會發現結果往往不理想。後來學界提出擴充版本的「套利定價理論」(APT),接受了非波動風險的獲利因子。事實上,就連支持過CAPM的Fama,也提出了FF3和FF5等多因子模型。
其次,CAPM強調「市場有效」,過度簡化實際狀況。注意,這裡不是討論市場效率本身,而是在說CAPM的假設比較狹隘,畢竟它建立在有效組合之上。因此,一旦市場無效或效率低,CAPM的假設自然不成立。
再者,我們根本無法得知個股的準確β,因此透過β來解釋報酬,注定會有誤差。順帶一提,這些誤差在後續理論中(例如APT),被解釋為α或ε(殘差),側面點出CAPM的不足。
記得我剛剛說的車隊冒險案例嗎? 對於系統性風險,CAPM認為投資者能得到回報補償,可是對於非系統性風險,理論上卻沒有任何回報。有些人可能會認為,這是理性投資的精神,可是我覺得這反而讓「風險和報酬」的解釋模式顯得無理。
CAPM受到的攻擊來自四面八方,還有許多從假設到計算細節的質疑,都在提醒我們不要迷信一套理論。然而,我寫出這些不是要抨擊CAPM,而是想告訴大家,即使是經典理論也有可能出錯。學而不思則罔,老派證券分析學徒也好,CAPM狂熱信徒也罷,一旦我們放棄了思考,接受既有框架,那麼或許很快就會被收割了。
7. 即將進入尾聲,我補充幾個比較具體的有趣論戰,但沒興趣的朋友可以往下跳一段。
「低波異象」。照理說,低波動(β)應該會對應到低收益,可是當我們檢驗數據時,很可能會發現α和β負相關,也就是波動風險越小的資產,反而有更高的超額收益,直接把CAPM的公式打爆。後來有人提出槓桿限制和「行為金融」層面的解釋,例如彩券偏好或虧損風險偏好,一定程度的解釋了低波異象。
「特質波動率異象」(IVOL)。CAPM認為非系統風險不會有相應定價,不過在計算單一資產的殘差時,有學者觀察到高IVOL往往代表著高回報。換句話說,本來看似合理的「聰明冒險」,變成了自以為聰明。行為金融同樣也在此有多處研究,我認為一些主流解釋都很值得參考。
我也知道,有人會提到1973的 Fama-Macbeth「二階回歸」。(見Risk, return, and equilibrium: Empirical tests) 而基於errors-in-variables(EIV)的懸而未決,反方認為這會造成統計偏差。直到1992 Shanken提出了解法,也就是著名的Shanken correction. 另外,從宏觀的角度來看,我認為由於當時Fama-Macbeth法著眼於CAPM而非APT,因此或多或少會有對β的依賴偏好。
8. 如果大家看完這篇文章覺得有道理,或許也該反思這些歷史理論演進的實用性。
對於資產配置者而言,CAPM或許沒有「實際意義」,畢竟既然都要採用市場指數投資了,我們還需要研究單一資產的定價嗎? 可是,我覺得各位朋友最好還是了解這套理論,為未來的學習和思辯打基礎。輕鬆來說,人類在眾多矛盾的理論當中找出最佳答案,就像在過河拆橋,不打破過去就無法迎接未來。CAPM只是一座古老的橋,但如果我們不屑走橋,很可能連過河都會失敗。
我的目標不是介紹一堆配置方式和定價模型,而是闡述一般投資人能夠輕鬆複製的投資框架。如果妳看過本系列的第一篇,應該知道我決心往「多因子配置」講過去,所以CAPM章節成為Markowitz之後的必然安排。當然,我沒接觸過相關課程,只是分享自己覺得順暢的推進路線,因此如果大家有更偏好的順序,也請相信自己的判斷。
這裡,讓我們先在探索資產定價的偉大航道上暫停,換個口味。
市場上充斥著機率,而投資者們的評估和最終決策,都需要承受失敗風險,在資產配置領域當然也是。因此,下一篇我會分享Bayes定理,而這又是另外一座橋了。
