简单性曾经是科学最求的最高目标

简单性曾经是科学最求的最高目标，从最早特勒斯认为万物源于水，将自然现象的复杂性简化的第一性原理，天文学家将复杂的行星运行轨道简化为规则且简单的球体运动，哥白尼在他的《天球运行论》也提到天球运动的基本模式是匀速圆周运动，牛顿和莱布尼兹发明的微积分，为运动模型理论加入了新东西，科学家可以计算一个物体的瞬时速度。

在牛顿的世界里，描绘了一副钟表宇宙的图景，设置好初始状态，然后遵循三条定律一直运作下去，只要知道宇宙所有粒子的当前的位置和时间，原则上就有可能预测任何时刻的情况。

这样还原论思维方式一直是占据科学的主导地位，还原论的最早提出者是笛卡尔，他是这样描述科学方法：“将面临的所有问题尽可能细分，细到能用最佳方法解决为止，依照特定的顺序引导思维，从最简单和最容易理解的对象开始，一步一步上升，直至最复杂的知识。”

大自然原则一直被看做一个确定轮的系统，只要知道初始状态，就可以预测和追溯每一时刻的因果事件。

以至于19世纪末，物理学家迈克尔孙说，大部分的基本定理都明确建立起来了。

三体问题导致的哲学转向

19世纪80年代后期，瑞典数学家依国王60岁生日的名义主办一个国家性数学比赛，题目是太阳系的系统是稳定的吗？拓扑学的先驱庞加莱也参与了这个挑战，他利用相空间模型，以证明太阳系系统是稳定的，他并未试图描述全貌，而把焦点放在简化的三体问题，相当于只关注相空间的一个切面，庞加莱最终赢得了大奖，但他的论文发布会，其他科学家仔细研究发现，庞加莱犯了一个错误，他的证明不成立。所以庞加莱在1890年发布了一篇修正版的论文，在修正论文的过程，庞加莱发觉自己的新方法证明了对于简化的三体运动，不稳定是常态，永久稳定的轨道则是例外。

从庞加莱的研究成果中，得到的最重要概念是，在某些情况下，几乎相同状态发展出的系统，可以很快演变出完全不同的结果。

此外庞加莱还发现，真实世界的系统对其初始状态十分敏感，而且是以非线性的方式变化。

1908年，他在《科学方法》中表示，初始条件微小的差异，将会最终现象的极大错误，这让预测成为不可能的事，我们只能面对偶然现象。在他看了天气也是不能预测的。

庞加莱的想法，并没有让气象学家放弃预测，关键是明白初始的观测必须广泛与准确到何种程度。而理查森就是挑战这一问题，他试图利用物理定律与数学近似算法，来预测天气，基本思路是讲地球表面划分为方格点，在上面测量气压与温度等资料，并向上扩展，然后计算每一个点与临近点的影响，如果点越近，大气的数学模型越准确，但受限于当时的计算能力，运算的时间比天气变化慢。

1959年，计算机开始登场，罗伦兹使用了一台 4000kb存储的计算机进行了模拟，他发现天气模型对初始状态十分敏感，即使差异小于千分之一，两次的模拟结果也完全不同，真实的大气对初始状态非常敏感，这样导致天气预测只能准确的 10-14天，他在1972年，提出了蝴蝶效应，混沌研究的核心课题，系统是否完全取决于初始状态。但是罗伦兹的发现只局限于气象学的领域。

生物学问题 - Logistic equation

为了搞懂混沌，我们需要先理解 Logistic equation方程，改方程是描述物种从一代到下一代数量的变化，为了简化，我们假设某种昆虫在冬天产卵后全部死掉，新生的一代在隔年的春天孵化出来。

开始昆虫数是 X，下一代是出生率决定，如果每只昆虫（不论公母）产生 r 个卵，那么隔年的昆虫数，就是

$$X_{n+1} = r X_n $$

如果考虑昆虫的死亡率，为了简化问题，使用 renormalization 技巧，考虑到昆虫的数量会有上限，我们将 X 的范围定位 0 与1 之间，为了反应未繁殖之前的死亡率就要乘上（1-X），这样的话

$$X_{n+1} = r X_n (1-X_n)$$

如果昆虫数 X 非常小，接近于 0 ，那么成长率就是 rX，不造成影响

如果昆虫数 X 非常大，接近于1，那么多数昆虫会饿死

如果将公式展开

$$X_{n+1} = r X_n - r X_n^2$$

因为有平方存在，所以昆虫的繁衍是非线性的过程。

生物繁衍会出现多种周期：

1. 如果 r > 1，种群将无法繁衍，导致灭亡。
2. 如果 3 > r >1, 将会产生吸引因子，种群数达到一个稳定的状态。
3. 如果 r > 3，运算次数足够多，将会出现两个不同，但各自固定的数值间隔交替变化。

通过计算机模拟周期3，出生率 r 值在 2.5 和 4 之间迭代 10000 次，可以得到一个分叉的图：

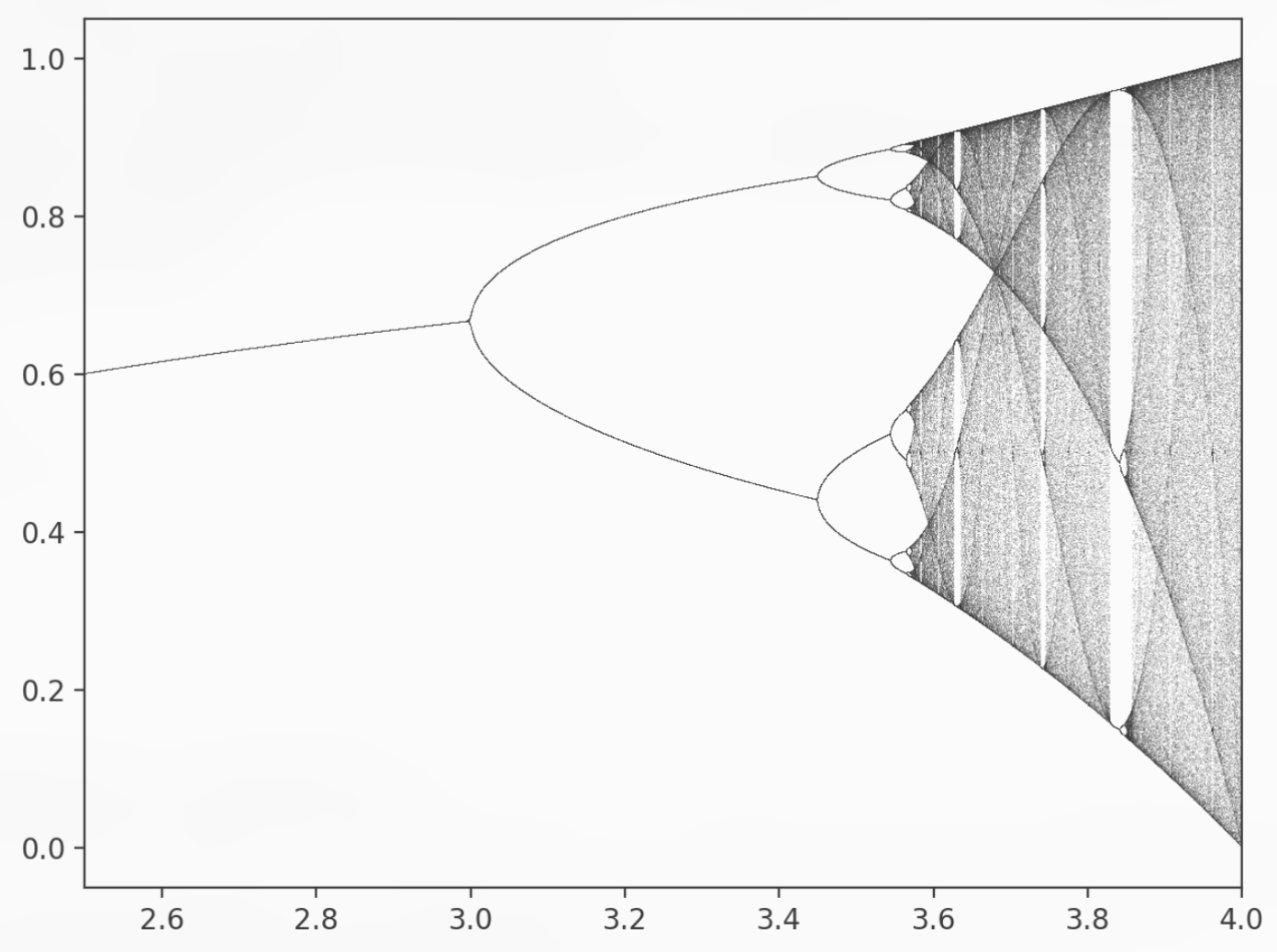
20世纪70年代，拥有物理学和生态学背景的罗伯 · 梅伊利用计算机模拟发现，当 r=3 时候出现分叉， r = 3.4495 时出现四种不同种群数中震动的系统（周期4），到 3.596，每个分支会再次倍增 16种可能性的种族群，找这里还是遵循简单决定式规则。

在 r> 3.5669时，种群数可能收敛到的吸引子有无穷多，进入混沌。

但是有意思的是在 3.9 > r >3.8 时，系统又回到了 r < 3 的稳定状态，放大看，得到了类似的分叉图形。同样的模式又再次重复，可以得到一个自相似的图形，这样的现象被称为自相似，在有序中存在混沌，而混沌中存在有序。

1973年，美国马里兰大学为了打破科学家之家藩篱，设立了扩学科的物理科学与技术研究所，在其中工作的数学家约克与气象学富勒交谈自己从事非周期的研究，富勒推荐了罗伦兹在1963年发表的《决定式的非周期流动》的论文，约克立刻意识到这篇论文可以应用在气象学之外，可以用物理系统呈现，1975年，约克与李天岩发表了一篇名为周期3意指混沌的论文，混沌一词才因此出名。

他们的论文指出，如果某微分方式存在一个周期为3的解，那么比如存在无穷的周期解，他们提到的更多是有限混沌(limited chaos)，这样的系统是周期的。他们描述梅伊在逻辑斯蒂方式发现的行为模式。

在梅伊突破性发现的几年后，美国科学家费根堡指出，混沌具有更广泛的含义，依倍数进入混沌状态的不止是Logistic equation，还有生物种群的大小、电路的震荡、化学反应的震荡，还有经济表现的起伏循环，其中的重点是 “自引用”，如果符合这个条件，系统会依同一路径走向混沌，不是确定的，而是确定的。

有倍周期的方式达到混沌的例子有很多：

1. 滴水的水龙头
2. 河流的漩涡🌀
3. 电话传输数据的噪音（康托集合）
4. 分形

一些思考

1. 混沌可以来自于确定的系统，无需外部的随机源
2. 虽然混沌系统的具体变化是无法预测的，但是混沌中也存在秩序，比如倍周期，细节无法预测，但是更高的层面上混沌系统却可以预测
3. 对于混沌系统，对初始条件敏感依赖性。一些自然系统是没有问题的，比如预测行星的位置，即使预测不准确，也是八九不离十。但另外一些情况则完全不一样，比如预测非常多天之后的天气。

参考

• 《复杂》
• # 深奥的简洁
• # Logistic map - Master Math by Coding in Python
• # Using the Logistic Coupled Map for Public Key Cryptography under a Distributed Dynamics Encryption Scheme