Bayesian機率

為什麼,市面上的COVID-19 快篩試劑,都在強調「陽性一致率」有多高? 為什麼,在資產配置的系列文章中,我要重溫高中機率和統計? 投資有風險,而對於不可知的未來,我們可以使用模型來估算。然而只要是估算,就會有誤差,因此投資者應該與「不確定」和平共處,而不是夢想找到一個完美神準模型。在我眼中,一個有彈性的簡易框架,遠好過嚴格的複雜系統,在思想和投資領域皆然。
1. 讓我們複習統計和機率。
「頻率學派」統計,是傳統的統計方式。為了知道一件事的「確切」機率,傾向於不斷的重複實驗,並逼近真實機率的極限。例如我想知道骰子偶數的機率,最簡單的方式就是丟很多次。換句話說,這個機率已經確定了,只是我們還不知道,所以手中的任務就是逼出這個數值。猜的準嗎? 不知道,但是我可以用「信賴區間」來描述。
至於「貝氏」框架,不認為結果是注定的,每個數值可能都是答案,因此人們往往會描述一個結果的「可能性」。換句話說,每一次的實驗,都有可能帶給觀測者新的結果,所以在此框架下會有「先驗機率」和「後驗機率」。非常粗略的說,由於從觀測者的「主觀」角度出發,這個機率會吸收新資訊而改變。例如我先假設骰子偶數的機率是0,可是丟一丟發現不對勁,於是把數值上調到0.8,後來又逐漸下修到0.5。
2. 說到貝氏,就想到「條件機率」和貝氏定理。
先定義P(A|B),代表B發生的時候,A發生的機率。例如我想描述闖紅燈而被撞的機率,就可以寫成 P ( 被撞 | 闖紅燈 )。
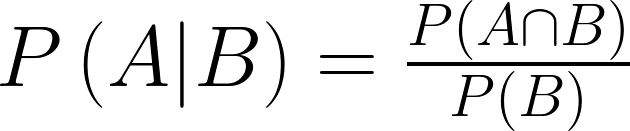
相對的,如果我想知道被撞的成因是闖紅燈的機率,可以用 P ( 闖紅燈 | 被撞 ) 表示。
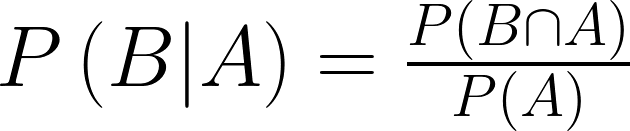
接下來,我們稍微整理公式。
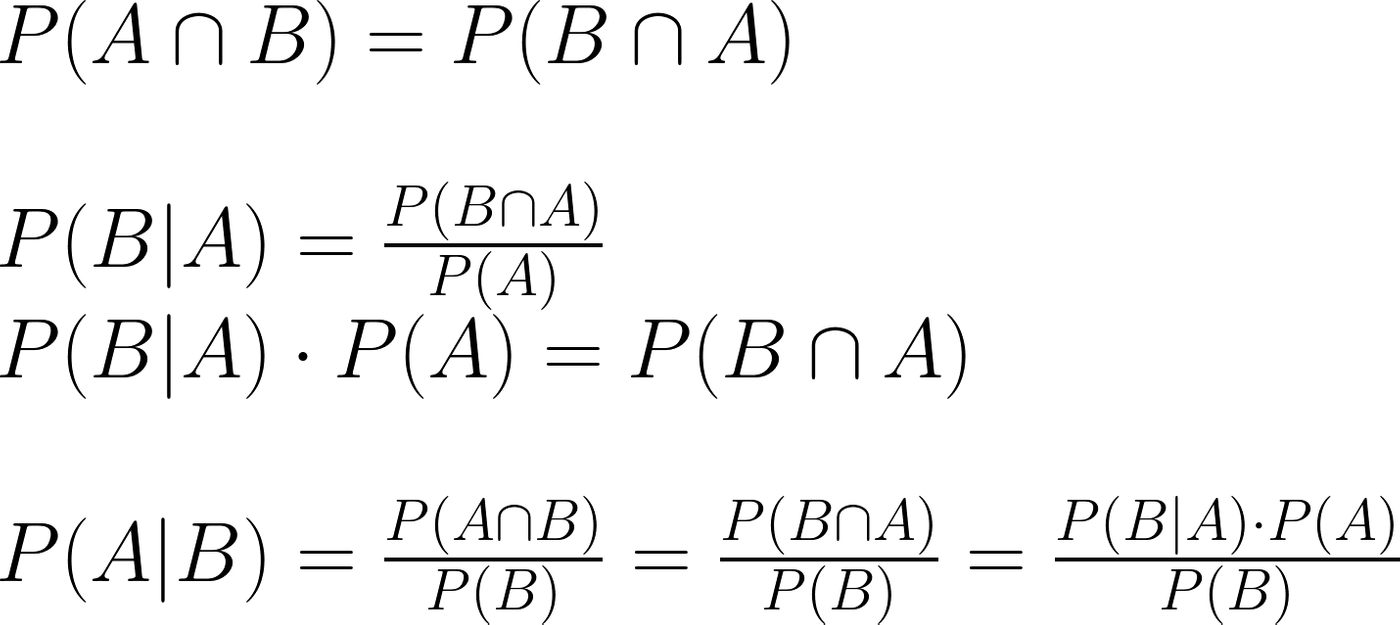
值得注意的是,P ( 被撞 | 闖紅燈 ) 和 P ( 闖紅燈 | 被撞 ) 是兩回事。換句話說,被撞有很多種可能原因,不一定只是闖紅燈。因此就算闖紅燈100%會被撞,也不能確定被撞就是闖紅燈。
3. Bayes是投資領域很重要的一個工具。
在生活中,有時候我們知道某件事情的可能性,就可以利用貝氏定理來回推相關事件的機率。從另一個角度看,我們也可以利用貝氏框架,導入自己的主觀推測。也就是隨著時間經過,不斷放進新的先驗機率假設,然後逐步修正模型。
因此,雖然我寫入Bayes是為了幫Black Litterman模型鋪路,但它的應用層面非常廣,例如機器學習中的簡單貝氏分類機。而對於資產配置,貝氏框架讓投資者有機會輸入自己的先驗模型,也就是主觀看法,所以從這個角度檢視,我認為Black Litterman比Markowitz法多了些彈性。
另外,關於先驗機率模型,有些人可能會想到Beta函數,畢竟它的參數簡單(兩個),但是結果多元。如果單純站在收益率的角度,Beta函數無用武之地,畢竟通常收益率比較趨近於高斯分布(嚴格來說不是,在此先放水)。不過對於統計數據的處理,Beta和Bayes的就很常合作了,而這也展現了模型的適應性。
我再說一個自己聽過的有趣例子,在利用基金淨值「逆向重建」投資組合的時候,我們依然可以使用Bayes幫助建模。有興趣嘗試的讀者,先驗可以用Dirichlet(可以當成多項版的Beta),後驗可以繼續用Dirichlet(也就是直接當成共軛)或嚴謹一些的隨機變分(stochastic variation)。
4. 最後來聊聊自己一些投資的想法。
既然本篇在說Bayes,就先從貝氏切入。有些人可能會看過貝氏推論的寫法P(θ|X),我們透過先驗分布和觀察數據,推論出新的猜測,而這也是投資者的學習過程。一開始的認知,會影響到後面的結果,因此保持更新的彈性,才能讓自己不容易掉入固執陷阱。
大家可能會意識到,貝氏框架天生帶有預測性質。我知道有些投資者(尤其是交易者),會告誡大家「不要預測行情」,可是這幾乎不可能。例如純多頭投資人可以不預測短期行情,可是他們希望長期而言市場會上漲。或是有人利用選擇權交易波動率,他們也會預測各種希臘字母。妳可以說,貝氏框架下的BL模型,帶有主觀意見,但我認為廣義來看,就連MV算出來的效率前緣和之後的CAPM,也帶有臆測。或許對於被動投資者而言,貝氏推論和收縮顯得無用,但我認為了解這些工具依然可以幫助自己。
另外,有時候我會聽到不同流派的信徒,因為不了解彼此而爭執,但這在我的眼中沒有必要。頻率學派框架下,我們很可能必須捨棄掉機率較小的結果,只保留看起來最適合的解答;但在貝氏框架下,我們可以用分布函數來表示不同觀點成立的機率,這也是我比較推崇的精神。是的,我也會批評別人的理論,但我會先了解對方的論據和論點,而且通常都是修正論述本身的漏洞,而不是研究方向。所以讀者會聽到我對於定投的抨擊,這是因為我有實際結果撐腰,也能看透理論本身的矛盾,但我從不會說一個定投者「錯」。就如同我認為股價波動不是常態分布,但我也不會排斥利用此函數的理論。
本篇簡述了貝氏精神,而在下一篇,我會介紹另一項資產配置的好武器,Black Litterman法。
