[leetcode]3319. K-th Largest Perfect Subtree Size in Binary Tree
※:這題是leetcode週賽419th的題目
二元樹是一種資料結構,每個節點(Node)最多有兩個子節點(left, right),而子節點又可以有自己的子節點……,這樣的節點組成就是二元樹,其中第一個節點稱為根(root node),沒有子節點的節點就叫做葉(leaf node)。
完全二元樹(Perfect binary tree)的定義是「每個leaf的層樹(到root的距離)相同,而且leaf以外的所有節點都有left, right兩個子節點」。
題目:3319. K-th Largest Perfect Subtree Size in Binary Tree
關鍵字:演算法、二元樹、遞迴
第一版
首先是準備測試資料,先照著題目的註解寫出TreeNode的結構方便測試,如下圖。
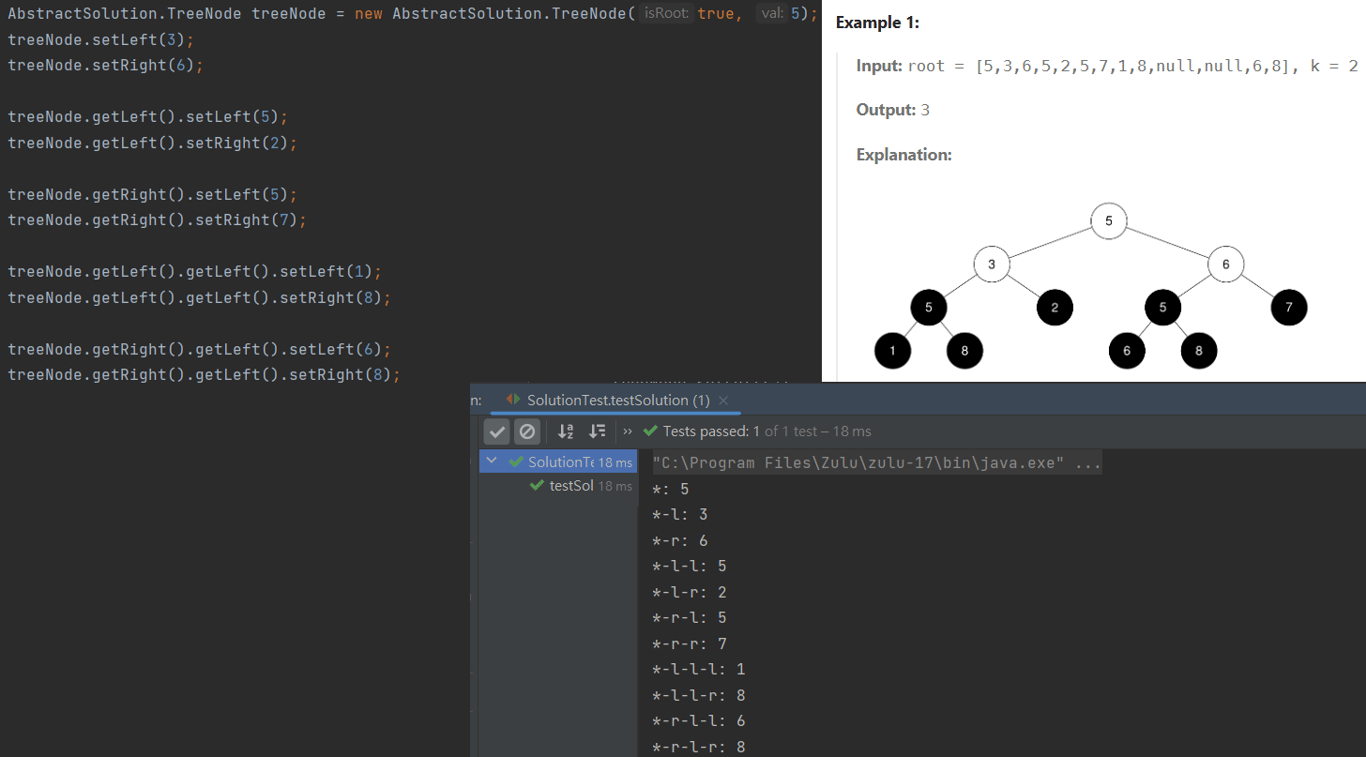
接著就是開始解題了。首先是關於完全二元樹的特性,「完全二元樹底下的每個子樹都是完全二元樹,所以一節點的左右子樹只要有一個不符合它就不是完全二元樹」、「每個leaf節點都是大小為1的完全二元樹」,因此從leaf節點往上判斷它的父節點還是不是完全二元樹,直到根節點為止每個點都檢查一遍,就可以得到總共有多少完全二元樹,以及個別的大小。
以下開始解題,照著題目的規則寫出檢查邏輯
// 完全二元樹的大小為1, 3, 7...,規則為「2的n次方-1」,所以只要計算深度就行。
// 同樣大小的二元樹沒有區別,記錄每深度的完全二元樹出現次數。
private SortedMap<Integer, Integer> result;
// 記錄總共的完全二元樹數量
private int perfectTreeCount;
private int countTreeNodesDepth(TreeNode root) {
// 子節點不存在不會列入計算,例如左子節點不存在表示左子樹的大小為0。
if (root == null)
return 0;
// 每個節點要判斷是否為完全二元樹需要等左右仔節點的判斷都完成才能進行。
int leftDepth = countTreeNodesDepth(root.left);
int rightDepth = countTreeNodesDepth(root.right);
// 如果任一個子節點的子樹不是完全二元樹,或者兩個子樹的大小不同,都代表這個節點範圍內的子樹並不是完全二元樹(回傳-1)。
if (leftDepth == -1 || leftDepth != rightDepth)
return -1;
// 符合的二元樹深度就是子樹深度再加1。
int nowDepth = leftDepth + 1;
// 記錄完全二元樹總數和該大小多一個,
result.merge(nowDepth, 1, Integer::sum);
perfectTreeCount++;
return nowDepth;
}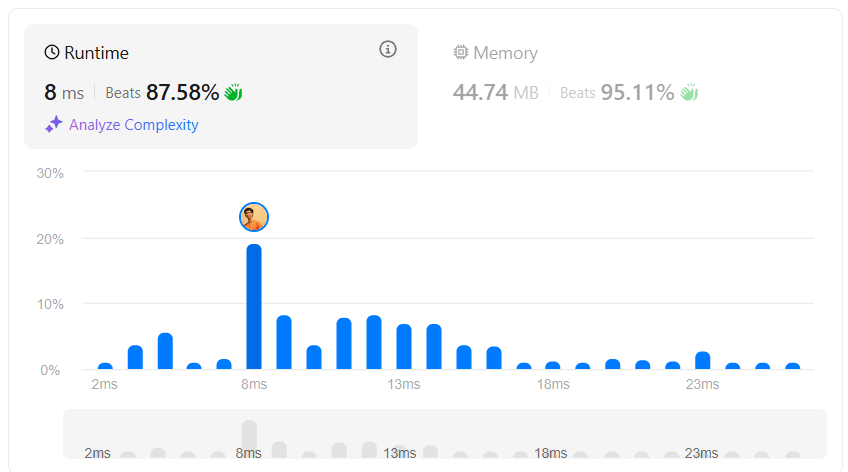
第二版,完全二元樹有三就有二,有二就有一
用SortedMap在新增資料的時候會經過排序,因此取出的時候可以用keySet()方法依據排序規則定義的順序取得每個值,那麼,是不是有更快的方法?
完成第一版之後想通了一件事「完全二元樹的大小一定是連續的」,層數三的樹當中一定包含二的,層數二的一定包含一的...
這樣一想就不需要排序,只要記錄著每個大小的完全二元樹有幾個,以及最大的是多大就好。
改動並不大,不用額外說明,總之改完之後確實有顯著提升效果。
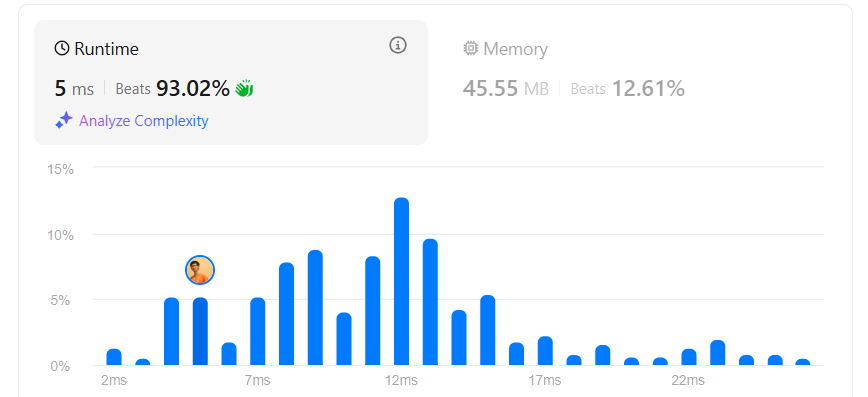
順帶一提我也嘗試過不要存層數1、2、3,而是直接存節點數量1、3、7,避免在最後才計算節點數量,但是這對時間沒有影響,因此不列出。
演算法類型的題目都可以當成益智遊戲來理解,最後找到的答案應該會是個不特別複雜、沒有太多例外狀況要判斷的做法,即使學會這類演算法本身不能為生活或工作帶來什麼改變(日常程式開發不會用到這麼高深的東西),但是理解好方法之所以是好方法的理由,也就比較不會寫出爛方法了吧。
有的人號稱開發經驗豐富,實際寫程式還是會出現同樣的邏輯重複出現,複製貼上了超過五千行,難讀又難改,就是因為這種基本概念都沒有,我就不該以為這是常識的。(怨念很深有感而發
