模型的估計誤差 (Estimation Error) 與近似誤差 (Approximation Error)

前言
在機器學習基本觀念:Bias-Variance Tradeoff 一文中,我們介紹了機器學習模型的 Error 包含了 Bias Error 與 Variance Error。當模型有很高的 Bias 時,我們稱為 Underfitting;當模型有很高的 Variance 時,我們稱為 Overfitting。
在閱讀本文之前,應該先理解機器學習基本觀念:Bias-Variance Tradeoff 中說明的概念,因為我們將會以另外一種角度來看模型的 Error。
訓練一個模型
假設我們希望擁有一個完美的模型,能夠 100% 準確的進行貓狗圖片的分類。這是一個相當基本的二元分類問題,我們通常會以監督式學習的方式來訓練我們模型。
在訓練模型之前,我們會先建立一個模型,模型架構的設計因人而異,也許是 5 層 CNN 再接上全連階層。此時的模型中的參數可能為隨機,也可能是由某一個機率分佈進行初始化,無論是哪一種,此時的模型都還沒有能力進行貓狗圖像的分類。
我們利用準備好的資料集,開始訓練模型。在訓練的過程中,模型內部的參數不斷的被調整,模型的 Error 也隨之下降。直到我們滿意,我們停止模型的訓練,得到一個訓練後的模型。
訓練後的模型內部的參數已經和原本截然不同,模型也能夠針對大多數的貓狗圖像做出正確的分類。
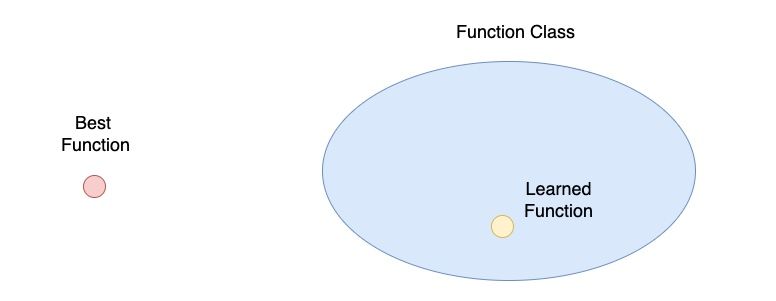
在上面的敘述中,我們歷經了三個步驟:
- 想要一個完美的模型
- 建立一個模型
- 訓練後的模型
其實這三個步驟就對應到上圖中的每一個元素。我們所希望得到的「完美模型」就是圖中的「Best Function」;當我們「建立一個模型」時,可以設計不同的模型架構,此時模型中的參數有無限多種可能,就是對應到圖中的「Function Class」;當我們訓練模型後,模型中的參數固定下來,所得到「訓練後的模型」對應到圖中的「Learned Function」。
估計誤差 (Estimation Error) 與近似誤差 (Approximation Error)
由上圖可以發現 Learned Function 其實與 Best Function 有一大段的誤差,這段誤差中就包含了估計誤差 (Estimation Error) 與近似誤差 (Approximation Error)。
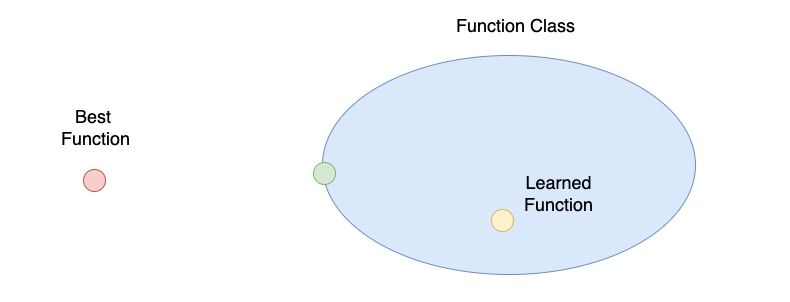
在上圖中,我們多標上了「綠色點」,用來表示在我們所定義的 Function Class 中與 Best Function 最接近的 Function。
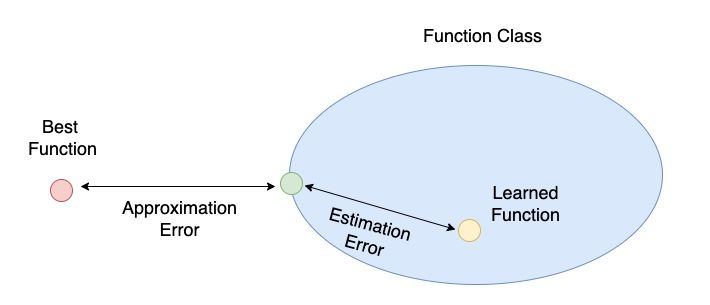
「綠色點」到 Best Function 的距離我們稱為近似誤差 (Approximation Error);「綠色點」到 Learned Function 的距離我們稱為估計誤差 (Estimation Error)。
如果我們定義一個非常複雜的模型,也就是一個很大的 Function Set,把 Best Function 都包覆進去了,那麼此時的 Approximation Error 會為零,但是 Estimation Error 可能會變得更大。相反的,如果我們定義一個非常簡單的模型,也就是一個很小的 Function Set,那麼此時的 Estimation Error 會很小,但是 Approximation Error 卻會變得很大。
不覺得 Approximation Error 與 Estimation Error 的關係,就像是 Bias-Variance Tradeoff 嗎!
結語
在本篇文章中,我們介紹了模型的估計誤差 (Estimation Error) 與近似誤差 (Approximation Error) 的概念:隨著模型愈複雜,Approximation Error 降低,Estimation Error 上升。
參考
- Stanford CS221 Lecture3
- Estimation versus approximation error
- What does the term “Estimation error” mean?
👣 👣 👣 我喜歡撰寫程式開發、資料科學領域相關的文章,希望可以透過簡單的文字解釋複雜的觀念!如果你也有興趣可以到我的其他平台逛逛哦!
👉🏻 DataSci Ocean
👉🏻 YouTube
👉🏻 Instagram
👉🏻 Potato Media
