「亚麻」我刷 994 ～ 烂橙子 🍊

基本信息

• 题号：994
• 题厂：亚麻
• 难度系数：中

在一个 m X n 的棋盘里，有各种橙子……

• 0: 代表格子里面没有橙子
• 1: 代表格子里面放了一个好橙子
• 2: 代表格子里面放了一个烂橙子

烂橙子可以按每分钟从上下左右四个方向污染相邻的新鲜橙子，问：究竟要等多少分钟，棋盘里的所有好橙子都会被感染成烂橙子？？？

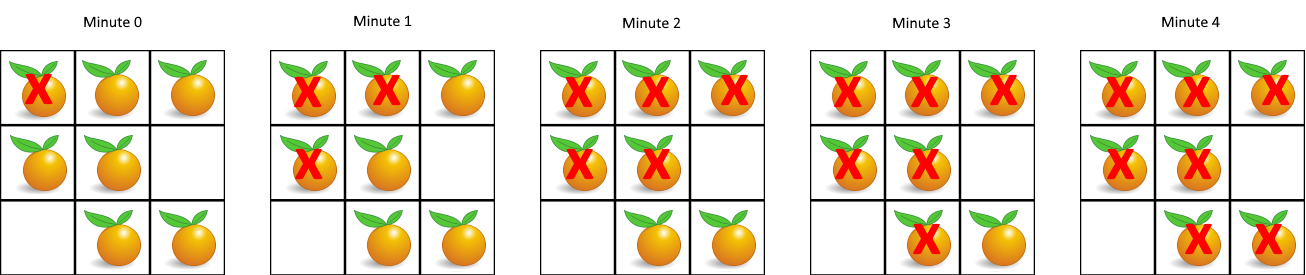
grid = [[2,1,1],[1,1,0],[0,1,1]]
返回 4

在 9 X 9 的棋盘里面有 1 个烂橙子；
1 分钟以后 1 号烂橙子感染了右边 2 号好橙子和下边的 3 号好橙子；
第 2 分钟，新加入的 2 号烂橙子和 3 号烂橙子继续向四周扩散……
以此类推，终于在第 4 分钟的时候，所有的好橙子都变成了烂橙子……
「游戏结束」返回 4

• 如果好橙子不能被烂橙子感染，返回 - 1:好橙子四周都是 0 与烂橙子不相邻；
• 当然，如果棋盘里面没有好橙子，那也无需研究烂橙子扩散问题，直接返回 0.

解题思路

• 欲解此题，需要从「烂橙子」为突破口研究——所有的橙子都是因为有了初始化烂橙子才会不断被感染的……
• 同时也需要关注一下好橙子——如果棋盘本身没有好橙子，也就没有后续了；
• 基于以上两点，我们先遍历一遍棋盘，统计一下橙子的情况。因为烂橙子是扩散中心，需要创建数组记录烂橙子的坐标值；而好橙子只要记录有多少就行了……
• 统计了好橙子和烂橙子数量后，我们把这道题转换为建立在矩阵模式下的「四个方向」广度查询遍历问题……

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        ROW, COL = len(grid), len(grid[0])
        
        # 统计烂橙子坐标和好橙子数量
        rotten = []
        fresh = 0
        for r in range(ROW):
            for c in range(COL):
                if grid[r][c] == 2:
                    rotten.append((r, c))
                elif grid[r][c] == 1:
                    fresh += 1
        
        # 接下来进入烂橙子扩散状态。需要满足 2 个条件：棋盘里面还有好橙子；棋盘还有烂橙子等待扩散……
        # 每扩散一轮，意味着时间过去 1 分钟……同时更新下一轮的烂橙子坐标
        minute = 0
        while fresh > 0 and len(rotten) > 0:
            next_rotten = []
            for (r, c) in rotten:
                directions = [(0, -1), (0, 1), (-1, 0), (1, 0)]
                for (dr, dc) in directions:
                    if (r + dr < ROW
                     and (r + dr) >= 0
                     and (c + dc) < COL
                     and (c + dc) >= 0
                     and grid[r + dr][c + dc] == 1
                     and (r + dr, c + dc) not in next_rotten):
                     grid[r + dr][c + dc] = 2
                     fresh -= 1
                     next_rotten.append((r + dr, c + dc))
            
            minute += 1
            if fresh == 0:
                break
            rotten = next_rotten
        
        # 结束循环返回前，需要检查好橙子是否为 0. 
        # 好橙子数量不为 0 说明遇上了好橙子周围都是 0 的绝缘状态——返回 -1  
        return minute if fresh == 0 else -1

Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

做题前可以向考官讨论：棋盘里面会不会出现没有烂橙子，没有好橙子的情况……

测试

• 好橙子与烂橙子绝缘状态
• ……

Big O

• 时间复杂度：O（n X m）我们遍历了所有的格子一轮
• 空间复杂度：O（n X m）最坏的情况，棋盘里面全是烂橙子，此时烂橙子数组长度为 n X m。

总结

• 看着信息量很大，仔细理清楚以后，思路还是很容易有的……
• 要牢牢记住「上下左右」四个方向查找的基础模板及核心思想
• 「烂橙子」作为亚麻经典高频题，一定要温故知新，彻底明白思路流程