如何投资庞氏骗局——再平衡策略原理
- 这是我们家的真实故事
多年前,当笔者还在念大学,两位家长中较激进的一位主掌财权,家庭主要积蓄在一个貌似高回报的庞氏骗局中基本亏光。从此,财权移交较保守的另一位家长,在未来的许多年,家庭几乎没有参与任何高风险、高回报的投资项目,更没有强迫大学毕业的孩子在落户的一线城市贷款买房。那个庞氏骗局中亏掉的钱,即使考虑通胀现在看来也微不足道。但那笔钱永久改变了家庭的投资风格。
- 一道心理统计课习题
有这样一个赌局,押上一笔钱,到期后,1/2概率赢回两倍(翻成三倍)、1/2概率输光。如果可以独立地玩很多局,是否参与?
(1) 家长A认为是这是有利的赌局,决定用所有的本金尽量充分地参与。多少局之后,家长A以99.9%的把握......亏光?
解答:
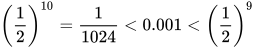
10局之后,家长A亏光的概率达到99.9%。
(2) 孩子B也认为是这是有利的赌局,但他只能决定10%的家庭投资,每局都是如此。N 局之后,如何计算家庭投资对数收益率的总体均值和总体方差?如何计算N 局投资平均到每局对数收益率的总体均值和总体标准差?
解答:
如果赢一局、输一局,收益率为[(100% +10% * 2) * (100% - 10% ) -100%]。(以e为底数的)对数收益率记为 log(100%+收益率),即 log(1.2*0.9) = log(1+20%) + log(1-10%)。注意到,对数收益率相加而不相乘。
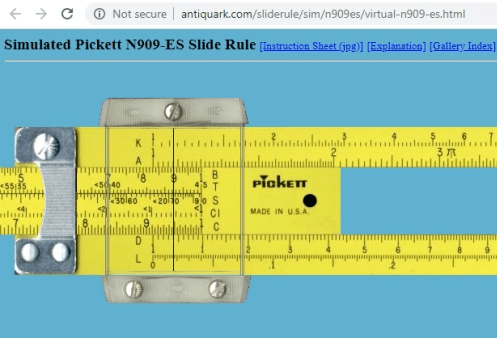
每局对数收益率以1/2概率为log(1.2)、以另外1/2概率为log(0.9)。第i局对数收益率 Y_i 的期望μ=0.038481,总体方差σ^2=E[ (Y_i - μ)^2] =0.02069。N 局之后,该投资的对数收益率
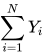
总的对数收益率期望为N×μ,总体方差为 N×σ^2。
平均到每局,
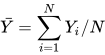
平均每局对数收益率期望为μ,总体方差为N×σ^2 / (N^2)=σ^2 / N,总体标准差为:
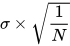
随着局数越来越大,平均到每局的对数收益率总体标准差越来越小,期望不变——这的确是一个有利的赌局。
(3) 多年以后,孩子B现在是家长C。C发现,这个赌局的庄家注定亏光钱,庄家为了维持局面,需要在赌局到期之前不断吸引更多的参与者押入本金。C还发现,不少庞氏骗局在庄家资金链断裂之前有1/2概率以200%的盈利退出,拿走三倍的本金。如果以固定的仓位投资这类庞氏骗局的特定阶段,200%盈利后结束撤出,否则就等它亏光。撤出或亏光之后,继续下一局。求每局最佳的仓位。
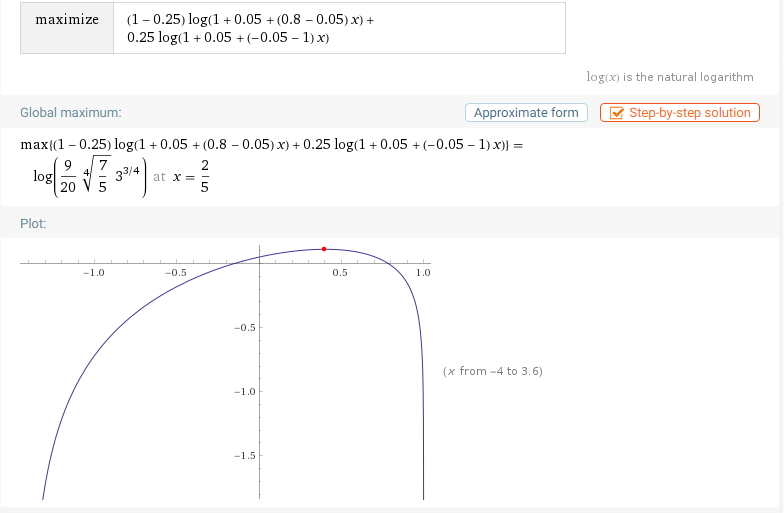
解答:C没有忘掉B在大学一年级的数学课。[log(1+2x)+log(1-x)]/2 的导函数是 [ 2/(1+2x) - 1/(1-x) ] / 2 。在最优仓位x =25%,导函数为零。
更一般的情形,如果实现q×100% 盈利之前庞氏骗局资金链断裂的概率是p,市场利率是r×100% (0≤ r<q),最佳仓位为
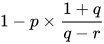
例如:r =0.05,p =0.25,q =0.8,最佳仓位 1-0.25*(1+0.8)/(0.8-0.05) = 40%。
- 最优仓位的操作化解读:再平衡策略
故事中的另一位孩子D最近发现,他竟然买了一个年报从未盈利的明星公司股票,而且四年来赚了不少浮盈。为了让D放心,C建议不妨先把这支股票的本金变现出来。本周四,这支股票开盘超过了埋单的卖价,成交之后摊薄成本摊到了负值。
然而C发现,卖出本金的策略可能仍然不妥。「从长远观点看,我们都会死」——凯恩斯可能不是这个意思,但我们持股的公司从长远观点看的确都会死,尤其是年报从未盈利的公司。它们是否庞氏骗局,并不要紧。如果卖出本金之后再也不搭理这支股票,仍然会在长远的未来见证归零。

这可能是习题最重要的启示:只要投资品下期对数收益率分布预判没有改变,最优仓位就不应当受本期盈亏影响而改变。如果本期不幸亏光了投入的25%仓位,在新的一期要再投入剩余75%本金中的25%,等于最初本金的18.75%。如果投入的25%仓位有幸盈利200%,浮盈等于最初本金的50%,就要变现出这笔浮盈的75%,保持下期仓位仍然为25%。这就是所谓的再平衡策略。
本文标题或许这么改会更准确:「如何投资注定归零的标的」。在比特币不到1美元的时候,在比特币接近700美元的时候,C都相信它会最终归零,同时还相信归零之前有不少于一半的概率涨上两倍。比特币是否庞氏骗局,并不重要。重要的是在200%浮盈的时刻,必须不太贪心地护持初心,变现浮盈的75%。然而以上并不构成任何投资建议,面对一万美元的比特币,C已经失去判断的自信。其实,大多数庞氏骗局的投资仓位算出来甚至小于零,这或许就是那些从岌岌可危的P2P机构疯狂借钱的坏人的算盘。
再平衡策略的习题推导用到了这样的假定:各期的对数收益率随机数相互独立。这差不多就是 Eugene Fama 的代表作标题——Random Walks In Stock Market Prices。C的大学室友E有幸师从 Fama 教授。2013年10月15日,E在朋友圈发了下面的喜报。如果想跟E老师学量化金融成为 Fama 教授的徒孙,可报读 fisf.fudan.edu.cn 的研究生项目。

- 写给耐心读者的文末建议
- 庞氏骗局付利息通常小于企图骗走的本金。在达到目标浮盈之前就归零的概率太大,往往计算出的最优仓位只是负值。「如何投资庞氏骗局」,大多数情形算出的答案其实是不投资。
- 模型中的目标浮盈率不是估算出的,是设定好的。唯一需要估算的是达到目标浮盈率之前的归零概率。这正是量化投资算法用武之地,也是不成功的算法取败之处。
- 目标浮盈率设置太低会导致归零概率太低,对小概率的量化估算容易差出数量级。习题中的算法通常只适用于不太小归零概率的高目标收益率情形,对应的最优仓位应当比较低。如果选品种时机的算法厉害,就能以较高频次重复低仓位×高浮盈率获得不菲的回报。如果选品种时机的算法错了,每一次的失败损失也可以获得控制,过多频次的失败可以及时提示算法要改。
- 其实前后期并不需要严格独立。只要各期的正相关不太高,平均对数收益率的标准差仍然可以收敛。如果有归零概率,绝不全仓。考试作弊,就是一种归零概率为正的全仓玩法。不要尝试任何作弊、不要情绪失控的时候跑进机动车道、不要在过马路的时候看手机。
