[leetcode]448. Find All Numbers Disappeared in an Array

題目：448. Find All Numbers Disappeared in an Array

第一版，建表記錄存在的數字

我的方法是使用布林陣列建個表，數字1存在就將表中的索引0標為true，反正數值最大就是N，我只要宣告個長度N的陣列就足夠使用。

不過這方法有些要求，首先建表必須知道表要多大，所以題目提供數字範圍的情況才可以使用；此外範圍太大也可能導致過多的記憶體消耗甚至超過題目限制；如果範圍很大但要記錄的數字不多的話也可能浪費較多空間。

這方法以這題的要求正好合用。輸入陣列的長度N在1~100000之間，其中數值的範圍在1~N之間，只要標示哪些數字有傳入，最後再檢查一次表中哪些數字沒標示過，收集起來就是解答。

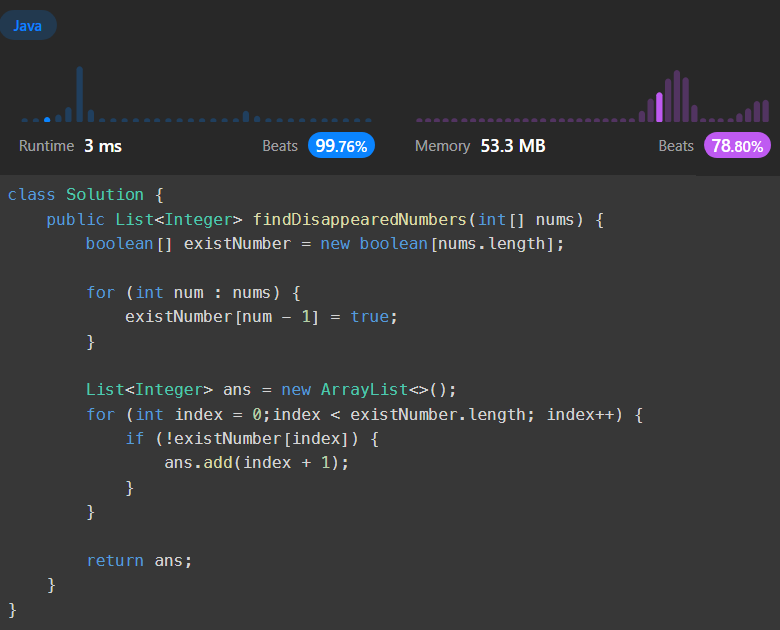
實際上後來也沒想到更好的方法，因此接下來就分享討論區看到的其他做法了。

其他方法，不使用額外空間的方法

這是寫在題目最後的敘述：「你是否寫出不使用額外空間，時間O(n)(線性時間)的做法？」我自己沒想到，所以這是參考自討論區的方法。

它並非在額外的空間標示該數字存在，而是在原本輸入的陣列標示，同時又不影響後續的判斷。

以輸入陣列為[4,3,1,1]為例：

第一個數字確認到4的存在，將第四個數字標為負數，以此代表4已記錄，陣列變為[4,3,1,-1]；
第二個數字讓陣列變為[4,3,-1,-1]；
第三個數字轉為正整數(畢竟沒有第'負一'個數字)再記錄，陣列變為[-4,3,-1,-1]；
第四個數字轉為正整數仍標在第一個數字，陣列仍是[-4,3,-1,-1]。

最後依序確認一次整個陣列，發現其中第二個數字是正的，也就代表前面的檢查中沒有發現過數字2，這就是解答。

將正負數判斷用絕對值函式精簡之後的程式和效率如下：

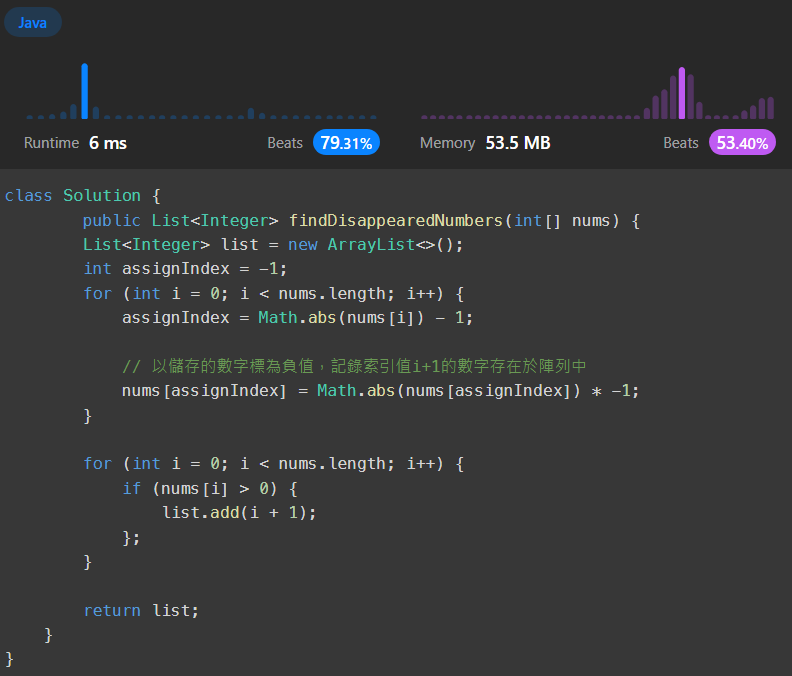
我的方法較快的可能原因有幾個，關於第一個迴圈將有傳入標記為true的部分，不只布林比整數的位元來的少，另外因為我的寫法是不加判斷直接寫true，少了一些判斷和計算的功夫；第二個迴圈檢查數字1~N是否在先前記錄過，純粹的true/false判斷也會比數字比大小的過程來得快。

至於明明不使用額外空間，執行結果使用的空間卻比我的方法略多的原因，我認為是在過程中計算使用的空間也被計算所造成的。

參考的討論區解答：https://leetcode.com/problems/find-all-numbers-disappeared-in-an-array/solutions/1583741/time-o-n-space-o-1/