複雜性是報酬預測的優點嗎？股票報酬預測：複雜模型 vs 簡單模型，哪一種比較優？

近年來，金融領域中人工智能的應用取得了顯著突破，尤其是在機器學習模型方面。人工智能不僅在投資組合構建和股票分析中得到了廣泛應用，還在股票市場收益預測中展現出巨大潛力。現有文獻中，許多研究傾向於使用參數較少的“簡單”模型進行市場回報預測。然而，本文通過理論分析和實證研究發現，相較於參數數量遠超觀測數量的“複雜”模型，簡單模型往往低估了收益的可預測性。本文將深入探討複雜模型在市場收益預測中的優勢，並解析其相較於簡單模型的潛在有效性。

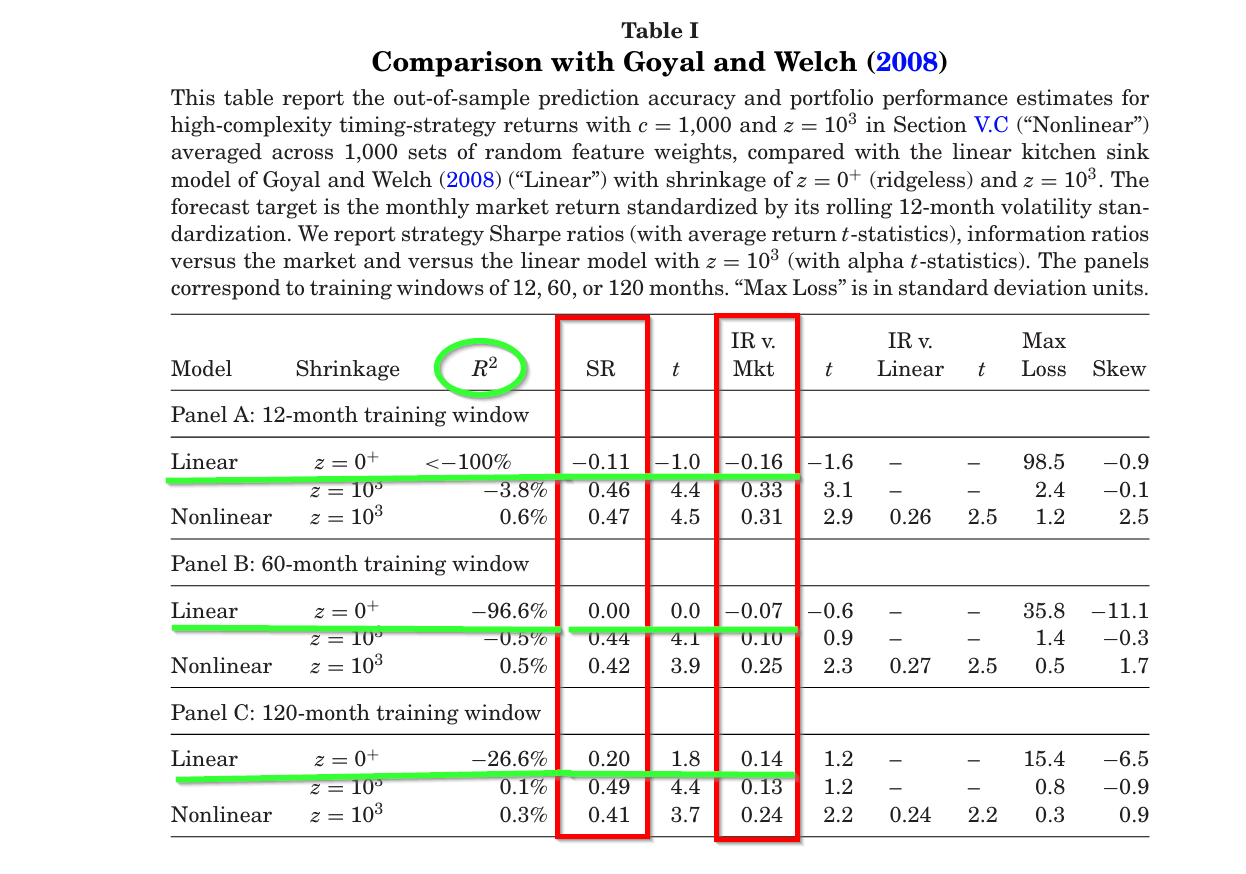
我們在所研究的所有資產類別（股票、債券、商品、貨幣和利率）中記錄了“複雜性的優點”。具體來說，每個資產類別的收益預測R²和最佳投資組合夏普比率通常隨著模型參數化程度的增加而提高。即使在數據極其稀少的環境中，複雜性的優點依然存在。模型複雜度與樣本外模型表現之間的實證關聯表現出與理論預測驚人的一致性。

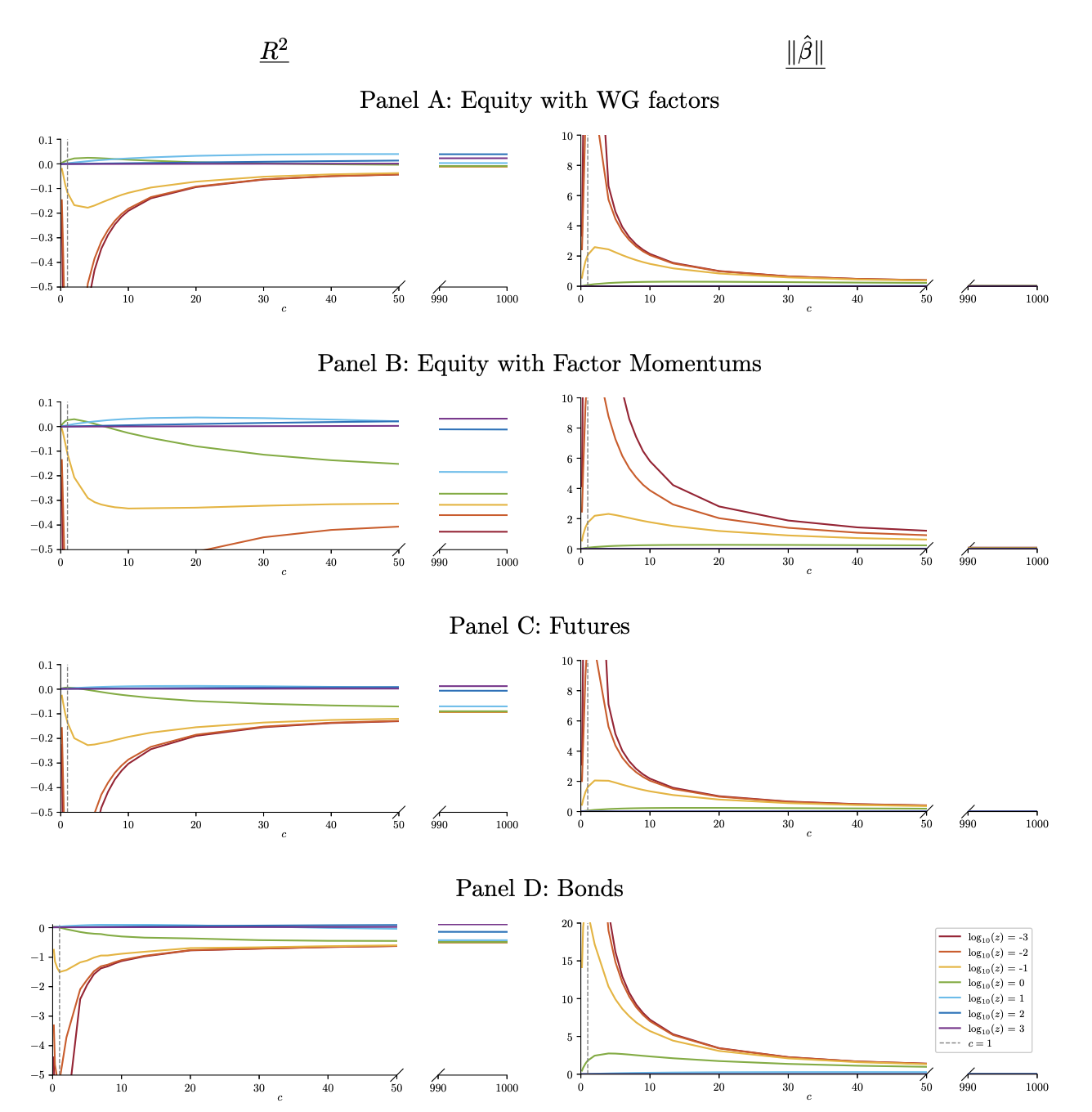
注：樣本外時機策略預期股票、期貨和美國國債的收益和波動率。

訓練窗口為 T = 12 個週期（股票因子和債券的一個週期等於一個月。期貨的一個週期等於一周，因為我們研究的是每周重新平衡的策略）；預測因子數量 L（或 cT）範圍從 2 到 12,000。這些數字報告了數據集中所有交易工具的數量 (47) 和 (48) 相等的平均值：(1) 對於股票因子，平均值涵蓋 159 個因子；(2) 對於期貨，平均值涵蓋 44 個期貨合約；(3) 對於美國國債，沒有平均值。

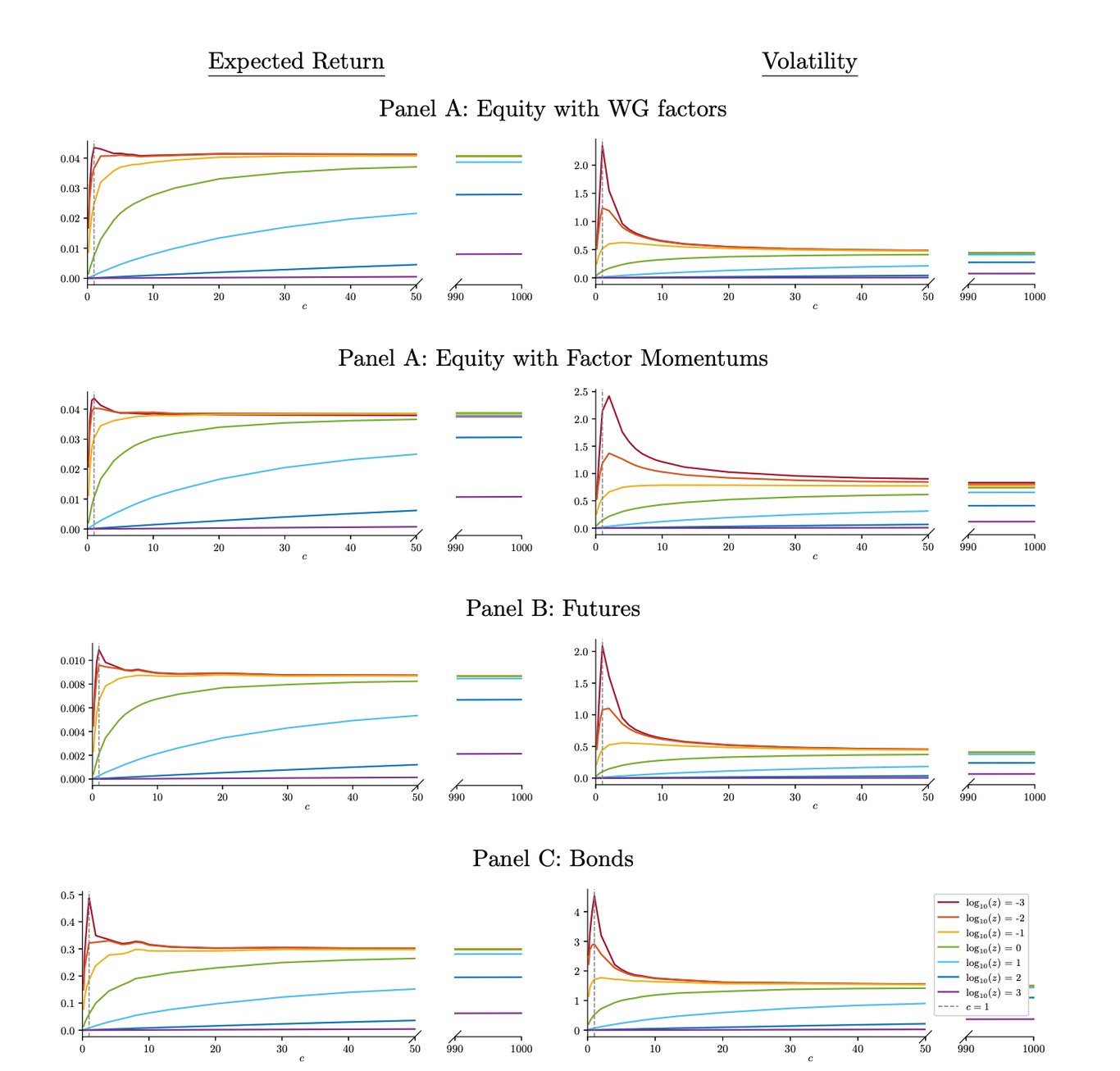
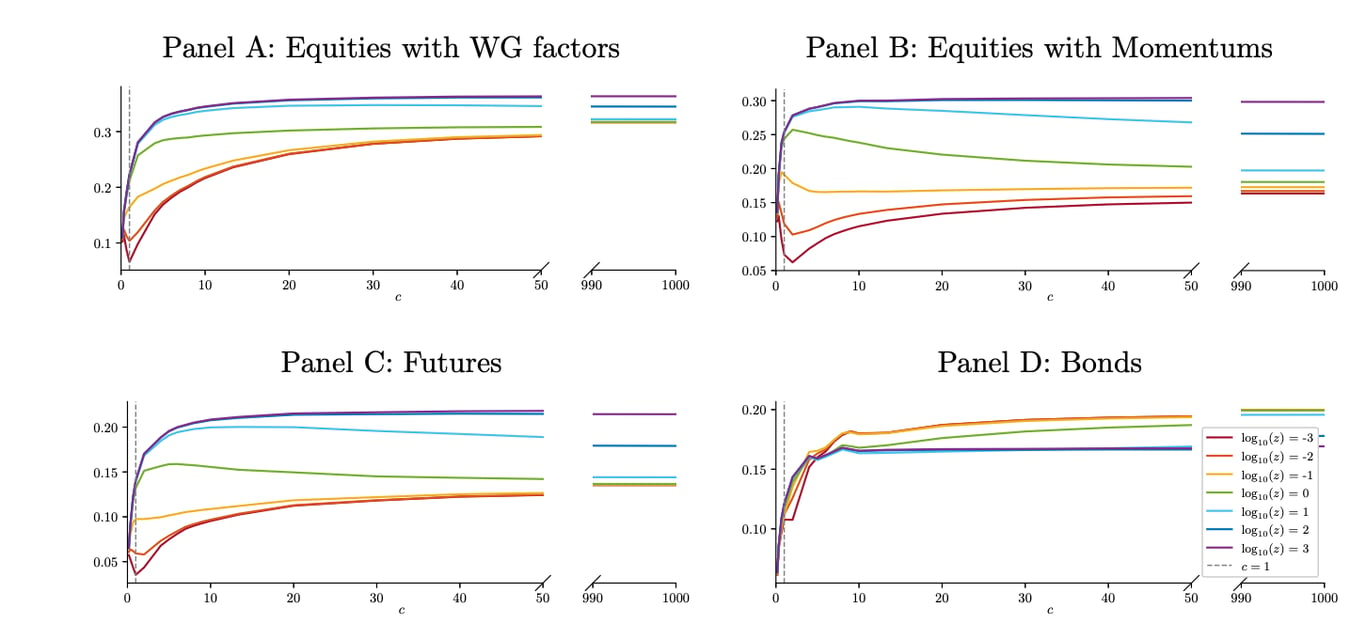
註：股票、期貨和美國國債的樣本外擇時策略預期收益和波動性。訓練視窗為 T = 12 個週期（對於股票因子和債券，一個週期等於一個月。它等於一周對於期貨，因為我們研究每週重新平衡的策略）；預測變數計數 L（或 cT）範圍為2 至 12,000。這些數字顯示了所有交易工具的平均數量 (49) 和 (50) 資料集：（1）對於股權因素，159 個因素的平均值； (2) 期貨，平均值跨越44 期貨合約； (3)美國國債沒有平均值。

研究目的

本研究旨在探討在高複雜度環境下（即當模型參數數量超過觀測數量時），非線性收益預測模型的表現。研究的資產類別涵蓋了美國股票、國際股票、債券、商品、貨幣和利率等。

1. 收益預測和最佳投資組合夏普比率的提升：

   • 隨著模型參數化程度的增加，所有資產類別的收益預測R²和最佳投資組合夏普比率通常會提升。這表明複雜模型能夠更好地捕捉市場的複雜性和變化，從而提高預測精度和投資組合的表現。

2. 複雜性的優點在數據稀缺環境中的體現：

   • 即使在數據極其稀缺的環境中，如樣本量少於二十但預測變量多達數萬的情況下，複雜模型仍然顯示出顯著的優勢。這一髮現挑戰了傳統的簡單模型觀念，表明在某些情況下，更多的參數可以提供更好的預測能力。

實證結果的一致性：

• 模型複雜度與樣本外模型表現之間的實證關聯表現出與理論預測的一致性。這進一步驗證了複雜模型在收益預測中的實用性。

結論

通過理論分析和實證研究，證明瞭複雜模型在市場收益預測中的巨大潛力。研究結果清晰地表明，無論是在數據豐富還是數據稀缺的環境中，複雜模型都能夠提供更高的預測精度和投資回報。這為投資者和金融機構在模型選擇上提供了有力的實證支持，促使他們在實際應用中考慮使用更加複雜的模型。

复杂模型在收益预测中具有以下显著优势：

1. 更高的預測精度

細膩捕捉市場細節：

複雜模型通常包含大量的參數和更複雜的結構，能夠對市場的細微變化和複雜動態進行更精細的捕捉和刻畫。因此，它們在捕捉市場中的非線性關係和異常現象方面通常表現出色，從而提高了預測精度。

2. 更佳的投資策略表現

提升夏普比率：

研究表明，複雜模型能夠提高最佳投資組合的夏普比率。夏普比率是衡量投資組合風險調整後收益的重要指標，較高的夏普比率意味著在同等風險下，投資組合可以實現更高的回報。因此，使用複雜模型可以幫助投資者建立更有效率的投資組合。

3. 適應數據稀少環境

複雜模型的穩健性：

即使在樣本量較少但預測變數較多的情況下，複雜模型仍能展現其顯著的優越性。傳統的簡單模型在面對少量資料時往往表現不佳，而複雜模型則能夠跨越資料稀缺的限制，提供可靠的預測。

4. 提升模型的彈性與適應性

動態市場中的優越表現：

市場環境是不斷變化的，簡單模型往往難以適應這種動態變化。複雜模型由於其更高的參數化程度和靈活性，可以更快速和準確地調整自身以適應新的市場數據和結構變化。

5. 捕捉非線性關係

發現深層市場法則：

市場中存在大量的非線性關係和複雜依賴結構，簡單模型可能無法充分捕捉這些深層的規律。複雜模型由於其非線性機制，能夠發現並利用這些隱藏的市場規律，從而做出更準確的預測。

更多內容歡迎關注花雨琦的Telegram頻道：@HuaHuaNotes