折現沒錯，但也請照顧未來的自己 - 關於雙曲折現（Hyperbolic discounting）

最近偶遇了一個概念：雙曲折現（Hyperbolic discounting）

它是認知偏差的一種，概括來說就是， 我們看重當下利益、低估長遠利益。得到利益前的延遲時間越長，對利益的價值評估便打越多折扣，兩者關係近似於雙曲線。

「當下利益優先」的現象大家都懂：堅持晨跑的對身心健康的益處抵不過賴床半小時的舒適，死線在下週的話不如先看一集劇再工作。但拖延真的可以簡單地用「看重當下利益」來解釋嗎？經濟學中的另一種折現方式是指數折現（exponential discounting）。這些數學模型一開始看得我一頭霧水，於是今天仔細研究了下，覺得很有意思！

其實「折現」本身，並不是認知偏差。正常情況下，本來就是當下利益優先，任何未來的收益都要做出折現。三年後的100塊可能只抵得上現在的80塊。

傳統經濟理論是利用指數性的折現。 例如第五期的利潤為x， 折現成第一期的利潤值就相當於𝛿^4x，其中𝛿<1就是兩期之間的折現率。指數折現有一個非常重要的性質：決策者在期初所建立的最適跨期決策，有其時間上的一致性。決策者做過相應的成本效益分析後，會優先執行淨收益更高的活動，放棄淨收益為負的活動。這個分析今天做和一段時間後做，得出的結果是一樣的。

然而心理學的許多實驗都發現人類（動物也是） 對較近未來的折現率，遠高於對遙遠未來的折現率。

例如，美國心理學家Ainslie做了這樣的實驗：

• 實驗的第一階段，人們可以選擇立刻得到$50，還是在六個月後得到$100；第二個階段，他們可以選擇在三個月後得到$50，還是九個月後得到$100。
• 絕大多數人在第一階段選擇立即拿到$50，而在第二階段決定多等半年而得到翻倍的收益。

問題在於，兩個選擇本質上是相同的。同樣的選擇放在三個月後，人們出現了完全相反的行為！

雙曲折現的重要特點是即時傾向性：在足夠遙遠的未來，決策者能夠對比回報與付出，做出明智的選擇，但在短期，我們更樂於逃避付出，及時行樂。

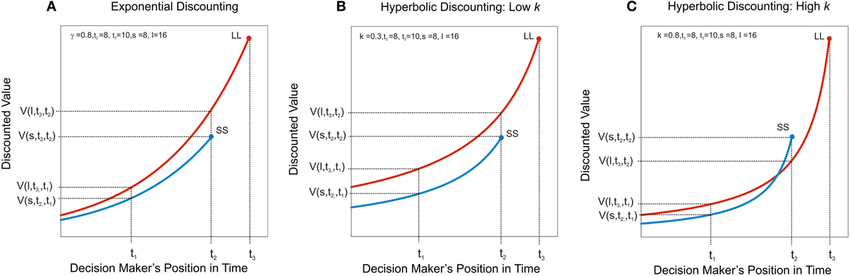
覺得上面的圖很有幫助——橫軸對應時間，縱軸對應收益——我用它舉個栗子：

• 假設紅線是去跑步，一小時後身體放鬆精神抖擻的收益曲線（長遠的較高收益），藍線是吃一盒冰激凌，半小時後糖分補足心情愉悅的收益曲線（短期的較低收益）。
• 圖A用指數折現，看到不論在什麼時刻選擇，運動的收益都是大於甜食的收益。結論：快去運動啦~
• 折現率k決定了雙曲線有多彎。圖B中在k還很小的時候，長遠的較高收益還是優於短期的較低收益。
• 圖C則是高k值的雙曲折現。隨著時間的推近，到了t2… 啊啊啊怎麼突然就甜食優先了xD？！

類似的例子有很多，對於好比戒煙、儲蓄、準備考試這樣會蠻辛苦的跨時決策，訂立長期目標的時候該怎麼選看得很清楚，但選擇近在眼前時，即刻滿足的選項突然變得無比誘人。

所以說，「當下利益優先」並不足以解釋拖延之類的選擇。雙曲折現的模型更能反映人們的行為：我們的決策不具有時間一致性。

換句話說，「此刻的自己」會做出和「未來的自己」不同的選擇。

在我們的幻想中，未來的自己更理智，更勤奮，更聰明。尷尬的是未來的自己並沒有變得那麼厲害。

這個模型在廣告和營銷中應用很多，在公共政策上的應用也很有趣（例如從工資中扣除養老金，公共場所禁煙）。在《簡介行為經濟學》裡讀到：「Laibson（1997）曾經利用一個可以用來近似（approximate）雙曲折現，但又同時擁有指數折現良好之數學性質的半雙曲（quasi-hyperbolic） 折現模型， 成功的計算出人的跨時儲蓄選擇行為。」

不明覺厲QAQ我得補課數學。

好麻煩吶 ><

未來的我會好好學習的吧。

參考：

陳 恭平 人非聖賢：簡介行為經濟學 http://idv.sinica.edu.tw/kongpin/teaching/micro/behavioral economics.pdf

Martuscello, J. (2017, December 17). New Perspectives into How Consumers Choose. (Behavioral Economics & HYPObolic Discounting). Retrieved from https://medium.com/@jasonmartuscello/new-perspectives-into-how-consumers-choose-behavioral-economics-hypobolic-discounting-ed399ec359b5

Story, Giles & Vlaev, Ivo & Seymour, Ben & Darzi, Ara & Dolan, Raymond. (2014). Does temporal discounting explain unhealthy behavior? A systematic review and reinforcement learning perspective. Frontiers in behavioral neuroscience. 8. 76. 10.3389/fnbeh.2014.00076.