用动态规化或者深度优先算法来数2英镑有多少种组合方法
IPFS
英国的英镑硬币有 1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), 和 £2 (200p). 比如我们可以用以下方式来组成2英镑
1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
问:一共有多少种方式可以组成2英镑?注意 不能有重复,比如 1英镑+2个50P 和 50P+50P+1英镑是一样的。
深度优先算法来数硬币
深度优先也就是 Depth First Search, 在计算机中是个很经常用到的搜索算法。我们可以假定以下函数 f(a, l) 来计算需要组成钱数 a, 上一个硬币的数值是 l 的方式总数。
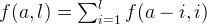
边界值 f(0, x) 上 1. 我们可以假定每一次选择的硬币不能比上一次的大。
function dfs(amount, last) {
if (amount === 0) return 1;
const coins = [1, 2, 5, 10, 20, 50, 100, 200];
let ans = 0;
for (let x of coins) { // 尝试每一种硬币
if (now - x >= 0 && x <= last) { // 不大于上一个硬币
ans += dfs(amount - x, x); // 递归深度优先
}
}
return ans;
}
console.log(dfs(200, 200));
通过计算 得到答案 73682. 当然我们也可以每次尝试不小于上一个硬币(相反方向)
function dfs(amount, last) {
if (amount === 0) return 1;
const coins = [1, 2, 5, 10, 20, 50, 100, 200];
let ans = 0;
for (let x of coins) { // 尝试每一种硬币
if (now - x >= 0 && x >= last) { // 不小于上一个硬币
ans += dfs(now - x, x); // 递归深度优先
}
}
return ans;
}
console.log(dfs(200, 0));
通过动态规化算法来数硬币
递归求解中间有一些节点会被重复计算,费时费力。我们可以用一个哈希表(或者字典)来存放这些已经计算过的值。很多情况下,递归+记忆就是动态规化了。
function dfs(amount, last, cached = {}) {
if (amount === 0) return 1;
const coins = [1, 2, 5, 10, 20, 50, 100, 200];
// 如果这个值已经被计算了
if (typeof cached[amount + "-" + last] !== "undefined") {
// 就直接返回值。
return cached[amount + "-" + last];
}
let ans = 0;
for (let x of coins) {
if (now - x >= 0 && x >= last) {
ans += dfs(amount- x, x, cached);
}
}
// 把这次计算好的值存起来以备将来调用
cached[amount + "-" + last] = ans;
return ans;
}
console.log(dfs(200, 0));
我们还可以用数组迭代的方式,来实现动态规化,以下JS代码就不需要任何递归,我们用数组f[x]来表示能组成钱币x的方案数,只需要两层循环累加计数即可。
function dp(amount) {
let f = Array(amount + 1).fill(0);
f[0] = 1;
for (let x of [1, 2, 5, 10, 20, 50, 100, 200]) {
for (let a = x; a <= amount; ++ a) {
f[a] += f[a - x];
}
}
return f[amount];
}
该算法的时间复杂度是 O(NM) N是硬币的类别数量,M是我们要算的总金额,空间复杂度是 O(M).
英文: How many different ways can £2 be made using any number of coins? (Depth First Search and Dynamic Programming)
同步到博文:https://justyy.com/archives/32222

喜欢我的作品吗?别忘了给予支持与赞赏,让我知道在创作的路上有你陪伴,一起延续这份热忱!
- 来自作者
- 相关推荐