实现拉格朗日插值方法 (Python)

 【还没研究过blogspot的排版方式，好像不能插入latex？所以先用截图来展示表达式了】

有高斯形状的分布函数:

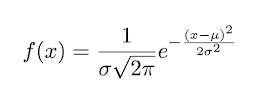
其中\mu = 50, \sigma = 15令x0 = 5.0, xn = 95.0, 在[x0, xn]范围内，等间距地选取 n+1 个值

以下为n = 2, 4, 6 时的多项式插值函数和原高斯函数的绘制代码：

#对高斯函数做拉格朗日插值近似

import numpy as np

import matplotlib.pyplot as plt

plt.rcParams['xtick.labelsize'] = 20

plt.rcParams['ytick.labelsize'] = 20

#绘制n=2,4,6时的多项式差值函数

x0 = 5.0

xn = 95.0

for n in [2, 4, 6]:

   x_arr = np.arange(x0, xn+(xn-x0)/n, (xn-x0)/n)

   y_arr = np.exp(-(x_arr-50)**2/(2*15**2))/(15*np.sqrt(2*np.pi))

   x = np.arange(x0, xn+0.01, 0.01)

   lk = [y_arr[i] for i in range(len(x_arr))]

   for i in range(len(x_arr)):

       for j in range(n+1):

           if j == i:

               continue

           else:

               lk[i] *= (x-x_arr[j])/(x_arr[i]-x_arr[j])

   Pn = sum(lk)

   plt.figure(1,figsize=(15,8),dpi=300)

   lbl='n='+str(n)

   plt.plot(x,Pn,label=lbl)

   plt.plot(x_arr,y_arr,'ko',ms=10)

#绘制高斯函数

x_arr = np.arange(x0, xn+0.1, 0.1)

y_arr = np.exp(-(x_arr-50)**2/(2*15**2))/(15*np.sqrt(2*np.pi))

plt.plot(x_arr,y_arr,label='Guass')

plt.legend(prop={'size': 16})

plt.grid()

______________________________

下图为output：

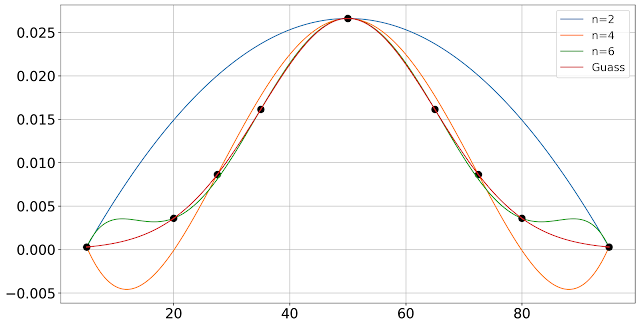
 下面附赠线性插值的画法，可以参考如何用python写分段函数。

代码：

import numpy as np

import matplotlib.pyplot as plt

plt.rcParams['xtick.labelsize'] = 20

plt.rcParams['ytick.labelsize'] = 20

#用线性插值法近似高斯函数

x0 = 5.0

xn = 95.0

for n in [2, 4, 6]:

   x_arr = np.arange(x0, xn+(xn-x0)/n, (xn-x0)/n)

   y_arr = np.exp(-(x_arr-50)**2/(2*15**2))/(15*np.sqrt(2*np.pi))

   #定义分段函数

   def fx(x):

       for j in range(n):

           if x_arr[j] <= x <= x_arr[j+1]:

               return y_arr[j]*(x-x_arr[j+1])/(x_arr[j]-x_arr[j+1])+y_arr[j+1]*(x-x_arr[j])/(x_arr[j+1]-x_arr[j])

           else:

               continue

   x = np.arange(x0, xn+1, 1)

   y = np.array([fx(t) for t in x])

   plt.figure(1,figsize=(15,8),dpi=300)

   lbl='n='+str(n)

   plt.plot(x,y,label=lbl)

   plt.plot(x_arr,y_arr,'ko',ms=10)

plt.legend(prop={'size': 16})

plt.grid()

______________________________

 下图为输出：

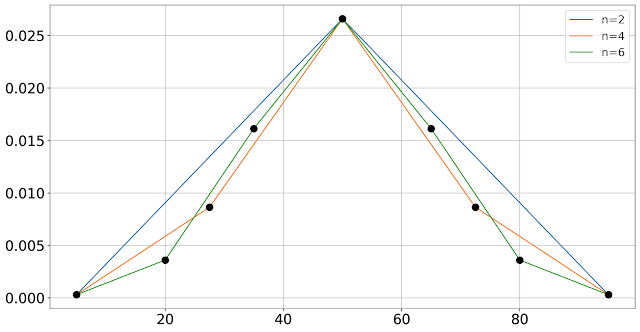
 以上禁止转载，仅供参考@奇特比喻