高等概率論筆記（3）無師自通的麻將與σ-域的生成

作爲一個四川娃兒，蓋碗茶，日光燈，竹馬甲，麻將聲，這四個意象構成了重要的童年回憶。幼時家裏老人去麻將館打麻將，爲了方便照看就會帶着我一起去。反正在那裏有近乎無限量的瓜子供應，還可以和其他的小朋友一起玩，滿地亂爬亂拱，倒也不會無聊。當然長輩是斷然嚴禁我們小輩學打麻將的，不過小孩子好奇心本來就重，越是禁止就越是躍躍欲試。看着大人四人一圈碼長城，時而沮喪嘆氣，時而欣喜若狂，而我們好像除了拿麻將牌來搭積木外就沒有別的玩法，久而久之，便就一起開始琢磨起麻將的規則來。

雖然長輩閉口不談麻將規則到底如何，不過一旦他們開打，便無暇再顧及我們在幹嘛了。所以我們有時就會默默地站在桌子旁邊看着大人打牌，耳濡目染，也就能夠捕捉到一些“碰”，“槓”，“胡牌”的一鱗半爪。於是，我們就會拿着一副麻將跑到沒人的雅間裏，煞有介事地根據自己聽到的支言片語，七嘴八舌的討論，自己發明了一套想象中的麻將規則出來。時隔多年，我們發明的兒童版麻將規則的具體細節已經記不太清楚了，不過大家玩自己發明出來的遊戲的那種單純的興奮，現在仍然歷歷在目。

我們在先前的筆記中談到過，從隨機事件的基本集出發構造σ-域的過程，本質上是利用隨機事件所能產生的所有可能結果來建立其一種合理的“玩法”. 這是大人玩麻將的方式. 而小孩在並不知道這套遊戲的規則的情況下，從有限的勝負觀察試圖重新構造一套自洽的遊戲玩法的過程，其實在數學上也是一個很值得研究的現象.

我們繼續以擲色子爲例，假如一個小孩子誤入賭場（未成年人嚴禁入內）暗中觀察一張賭桌的情況，他發現在這張賭桌上，只有擲出{6}的賭客獲勝了，那麼如果他學過一點σ-域的定義的話，他應該就能反推出整套遊戲規則：這裏很有可能是在玩猜六點 F = {∅, {1, 2, 3, 4, 5}, {6}, Ω}.

不過不要輕易被這個例子蒙蔽了，對σ-域的重建會輕而易舉地變得相當復雜. 例如，如果我們告訴你子集{A₁: 1, 2, 3}和{A₂: 1, 3, 5}都是某個σ-域的元素，並要求你重建包含A₁,₂的最小σ-域，我們從A₁和A₂出發，反復利用σ-域的定義2和定義3加入必要的子集元素，最終會獲得一個包含16個子集的子集簇F.

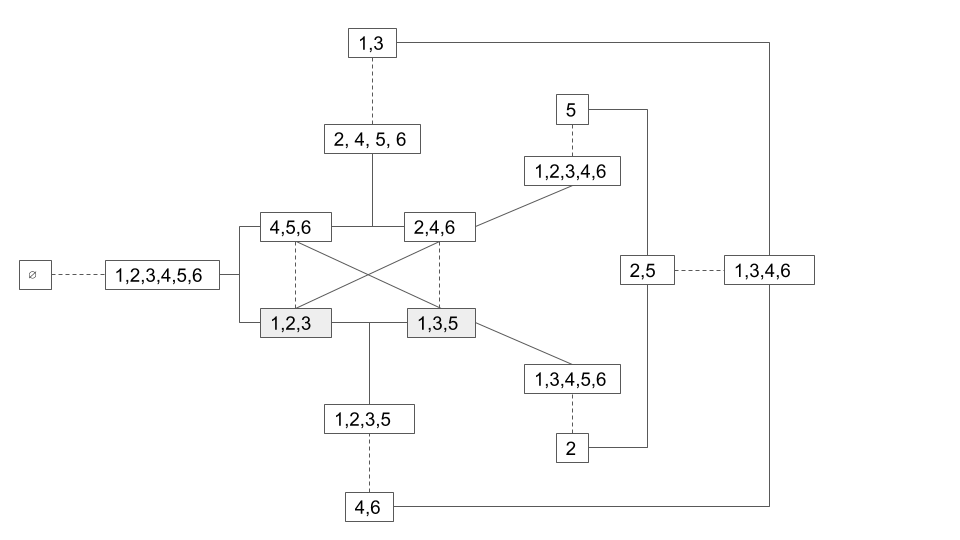
需要注意的是，在這裏添加“最小”這一限定條件是有必要的：我們顯然可以看出能包含A₁,₂的σ-域並不唯一. 比如，由基本集的冪集P(Ω)所構成的σ-域就必然包含A₁,₂，但是P(Ω)的計數測度顯然遠大與我們手動構建的σ-域. 在崇尚簡潔的數學中，顯然這個最小σ-域的性質更值得我們關心. 我們將它稱之爲由子集簇A = {Aᵢ}生成 (generate) 的σ-域，並簡記作σ(A).