機械學習2
延續上一章
架設出一個模型後我們把圖片丟進去,他只會跑出一個不三不四的結果。
那該如何去條整模型weight和bias呢?
面對如此之大的函數我們不可能自己手動調整。要調整要先有一個標準去判斷模型的好壞,在機械學習中使用cost function來判斷模型的好壞,cost function的計算方法是將模型給出的每張圖片的結果減去你預計的每張圖片的結果的平方和的平均。所以函數的值愈小模型愈好

我們的輸入是圖片的每個像素的灰階值,輸出是0~9。亮度代表是這個答案的可能性。
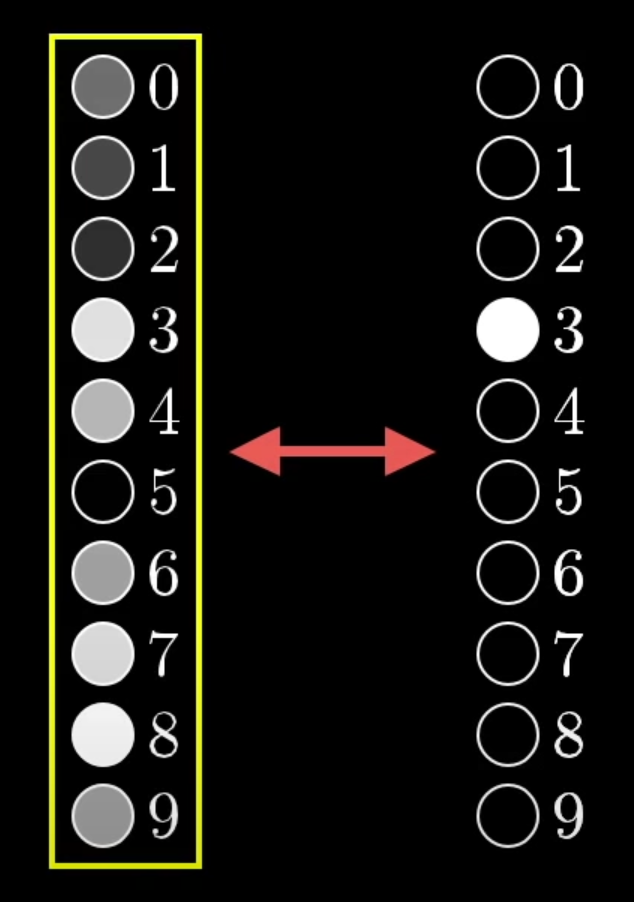
現在目標就很明顯了,就是要靠調整weight和bias去求出cost function的最小值,讓它對每一張圖片給出的結果都是正確的。
那要怎麼去求出最小值呢?
求最小值就是求函數最低點,在國高中教的二次函數四次函數可以輕鬆求出最低點,但是在機械學習中有成千上萬的自變數,不說求出最低點,連話圖都是個問題。
所以在機械學習中使用了微積分的梯度下降法去求出最小值。
可以想像你在一座山上你想要下山,而梯度會告訴你最快的上山方向反方向就是下降最快。

現在你要做著過山車下山去到最底點,如果你的速度太快的話可能跟下圖一樣滾來滾去找不到最低,但是如果速度太慢那可能過了一天都還沒到半山腰。
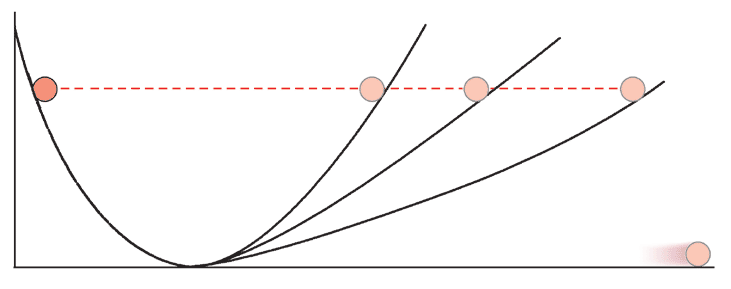
找出適合的速度後就可以尋找最底點了,我們用走一步看一次斜度的方式看看我們是不是到了最低點,如果走到了平地基本上就是函數的局部最低點了。
現在我們找到了一個最低點,但是這真的是最低點嗎?
我們的函數可能長這樣
有可能你只是走進了其中的一個坑而已,不是到了真正的最低點。
但是有時局部最低點就足夠給出一個不錯的結果了。
那該如何用梯度求出最低點?
對所有的weight和bias求反梯度後會告訴你,
告訴你調整哪些數對cost function的影響比較大,上升多少或是下降多少。
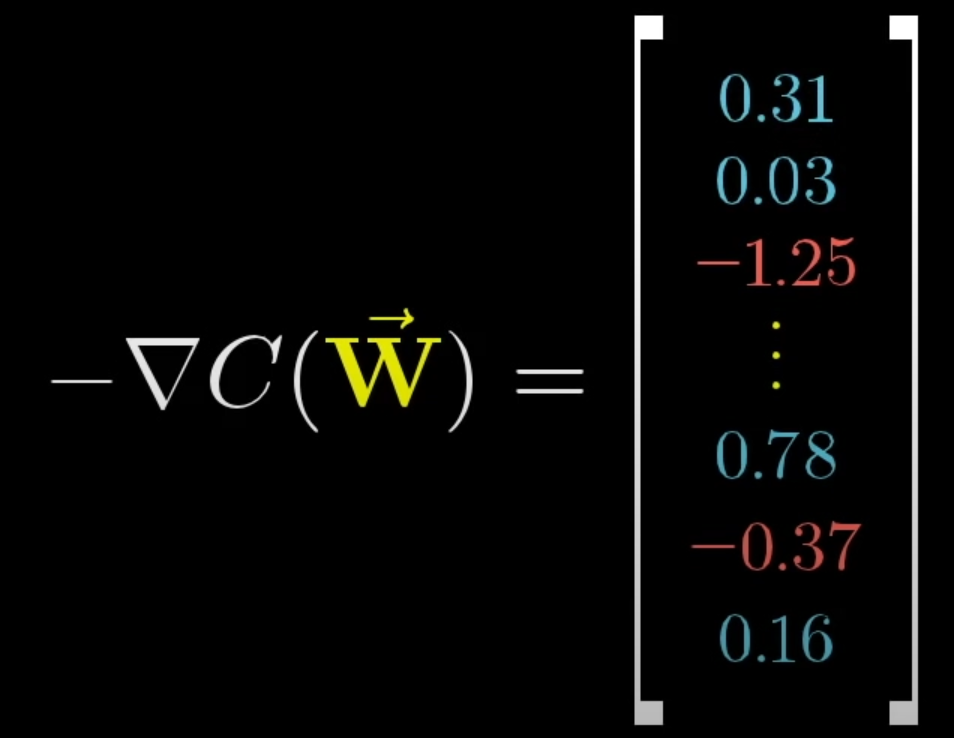
一直求梯度然後下降,透過這種方式就可以將cost function降低,但是每次都對全部的數據求梯度好像有點浪費時間。所以通常會使用batch,將資料分成小塊然後對小塊的資料求梯度,雖然不會是那麼完美的下山路線但每次都會有一定的近似值。
這種方法叫隨機梯度下降,可以用來加快速度。

資料:https://www.youtube.com/watch?v=Ilg3gGewQ5U&list=RDCMUCYO_jab_esuFRV4b17AJtAw&index=6
喜欢我的作品吗?别忘了给予支持与赞赏,让我知道在创作的路上有你陪伴,一起延续这份热忱!




