Mythos Lullaby - Kosmos Flatland (Part I)
神話的搖籃曲 - 平面神話秩序 英文版
Petreon: https://www.patreon.com/posts/92198393

The Mathematician's Tombstone
A long, long time ago, a stranger passed by a small town not marked on the map. He saw three tombstones in a cemetery outside the town, which read:
| Mathematician's Father ◭ | Mathematician's Mother ◮ | Mathematician Daughter ▲ |
There were still fresh flowers in front of the tombstones, not yet withered.
As someone interested in mathematics, the passing traveler took out his mobile phone and searched online for the mathematical achievements of the "Mathematician Daughter".
However, he couldn't find anything on the internet. He couldn't find anything on the most advanced search engines, he didn't get an answer from the most advanced AI, and he couldn't find any trace of the "Mathematician Daughter" in all academic paper databases.
Frustrated by the data desert, the traveler decided to enter the small town and ask the local people about the mathematican family.

The Town's Past
This is a peaceful small town, the residents are not wealthy but live in peace.
The center of the town is a temple, the traveler has no idea which deity is worshipped in the temple.
He found a very old man in the square outside the temple, who was feeding pigeons at the time.
Traveler: "Excuse me for the interruption, do you know the town's past?"
Old man: "Hello stranger, I have lived in this town for a very long time and remember most of its past."
Traveler: "I saw three tombstones outside the town, which read 'Mathematician's Father', 'Mathematician's Mother', and 'Mathematician Daughter'. Do you know anything about this family?"
Old man: "Of course, although the descendants of that family no longer live in this town, their story has left a deep impression in my mind."
The Old Man's Memories
The "Mathematician Daughter" was the youngest daughter of the family. The parents, although not well-educated, were kind and hardworking people with a good reputation in the town. Their other children had grown up and lived in different places. Unexpectedly, they had a little daughter in their old age.
They cherished their little daughter very much.
The little girl was naturally lively, optimistic, active, and full of curiosity.
From a young age, she had a dream - to become a philosopher, astronomer, and mathematician like Hypatia [1].
The little girl would imagine what Hypatia would have been like in history, the cultural customs of the people at that time, what the night sky of Alexandria would have been like, etc.; she would also grieve for Hypatia's death.

Although the little girl's dream was to become a mathematician, her talent seemed not to lie in mathematics. She usually just merely passed the school's math exams. She spent a lot of time improving her math exam scores, but to little avail.
On the other hand, the little girl had obvious talents in music, language, and sports. She was found to have perfect pitch at a young age, and she could reproduce the music after hearing the melody once or twice.
Whenever the girl was upset, she would quietly look at the stars alone, humming the tunes she had heard. Sometimes she would dance by herself, spinning and spinning until she was dizzy.

The girl still did not give up her dream of mathematics. She used her pocket money to buy some books related to mathematics. One of them she loved very much and often shared the stories with her friends.
This storybook, called "Flatland" [2] [3] [4].

The Traveler's Trance
When the old man mentioned the book "Flatland", the stranger fell into a trance.
The traveler knew about "Flatland", he had read it, and remembered that there were several adapted movies of this book, which was published in 1884.
The author of this book is Edwin A. Abbott [5], born in 1838 in Victorian England, studied classics, mathematics, and theology at Cambridge University. He was an Anglican clergyman, devoted his life to education and spiritual pursuit, and loved Shakespeare.

"Flatland" is a story that describes the life of a square named A-Square living in a two-dimensional flat world.
In the new millennium year of 2000, A-Square encounters a visitor who claims to be from a three-dimensional world. Subsequently, A-Square's worldview is overturned.
It has been adapted into several different versions of films [6] [7] [8] [9].
Flatland (1965) - https://www.youtube.com/watch?v=yBbZmwROv84
Flatland (TED) - https://www.youtube.com/watch?v=MGv8MMi8QO0
Flatland (2007) - https://www.youtube.com/watch?v=avMX-Zft7K4

Social Hierarchy in the Two-Dimensional World
In the memory of the traveler, the protagonist of "Flatland", A-Square, is a square and a lawyer. By the start of the story, he is already a grandfather with several grandchildren. A-Square's memories and self-narration form the content of the entire book.
In the two-dimensional world where A Square lives, one's social status is determined by the number of sides of their geometric body shape.
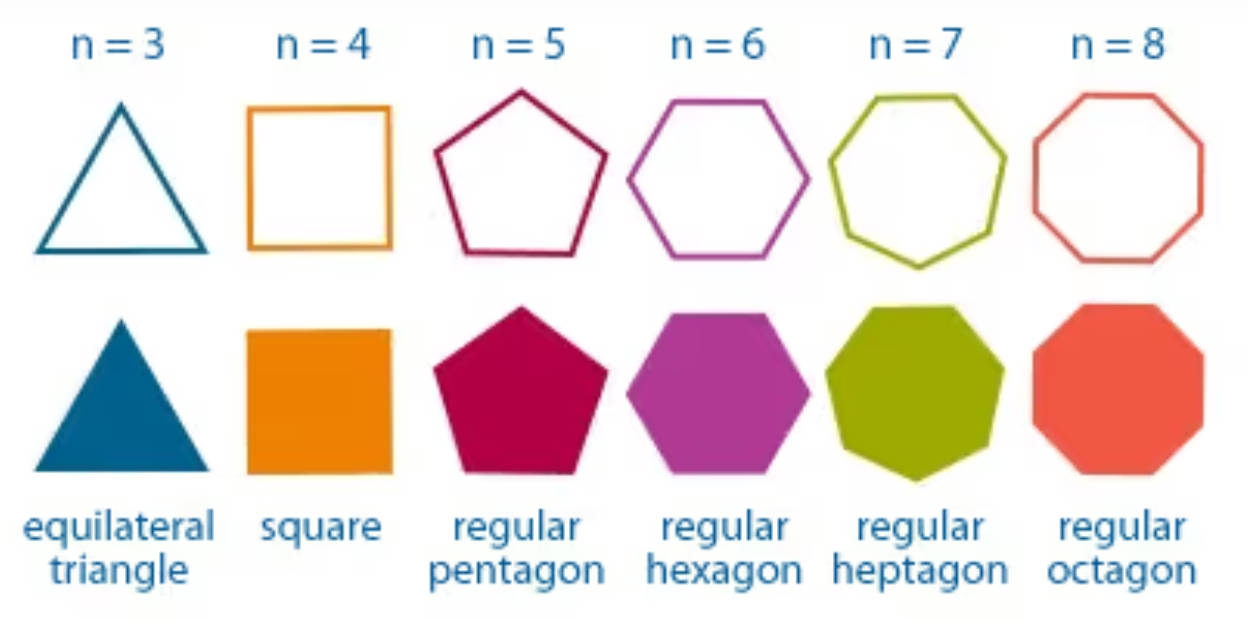
A square has a higher status than an equilateral triangle, a regular pentagon has a higher status than a square, a hexagon has a higher status than a pentagon, and so on.
In the social order of this two-dimensional world, the closer the flatlanders are to a Circle, the more perfect, wise, and noble they are considered. Those who approach the shape of a Circle, like a regular 100-gon or 200-gon, are seen as near-perfect and belong to the highest class in the social order - the Priests.
As a square, the protagonist A-Square belongs to the middle class in this social order.
In this social order, polygons with equal sides are praised and admired, while irregular polygons are considered inferior, of poor quality, and even deformed.

Four Directions: East, South, West, North
Just like the three-dimensional world, the two-dimensional world has four directions - East, South, West, and North.
For the inhabitants of the two-dimensional world, the North is "UP" and the South is "DOWN" (the two-dimensional world does not have the concept of UP and DOWN, these concepts only exist in the language of the three-dimensional world).
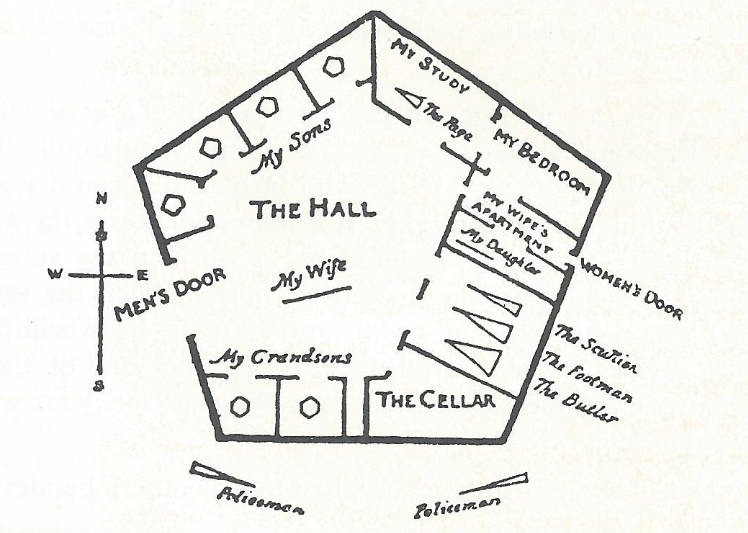
Most people of two-dimensional world live in pentagonal houses, the shape of the pentagonal housing is a legal requirement. As the angles of a pentagon are > 90 degrees, not so sharp, and therefore not so dangerous for pedestrians. The roof faces North, and the bottom faces South.
The following is a three-dimensional overhead view of a house in the two-dimensional world.
Phenomenal World: One-Dimension, All Things are Lines
In A-Square's world, what people can see with their eyes is actually only one kind of geometric shape - a line.
Just like a very thin, thin, thin coin, looking down from above, it is a circle, but if you spin the coin 90 degrees, you will see its side is close to a line.

So what A-Square sees every day is a line, what he touches is a line, and the sound he hears is also reflected by a line.
Apart from lines, there is nothing else.
In the two-dimensional world, their senses are one-dimensional (touch, vision, hearing).
So how do the people of the two-dimensional world distinguish different geometric shapes?
They mainly use three senses to distinguish geometric shapes: hearing, touch, and vision.
Perceptual Skill: Auditory Recognition
In the two-dimensional world of Flatland, although hearing is used to identify different residents, it is difficult for it to accurately identify a person's geometric shape compared to touch and vision.
The inhabitants of the two-dimensional world do not have echolocation organs and perception like dolphins, whales, bats, and other animals. These amazing animals can actively emit high-frequency sounds and use their echoes to locate the distance, position, and shape of an object.
The inhabitants of this world also have not developed radar technology capable of identifying the shape of objects - "Flatland" was published in 1884, when the concepts of radar and sonar did not exist, and the ability of some animals to echolocate was not yet discovered by humans.
Thus, in the two-dimensional world where A. Square resides, hearing is far less effective in identifying shapes than touch & vision.

Perceptual Skill: Tactile Recognition
In the two-dimensional world, touch is the simplest way to distinguish shapes. Different geometric shapes have different angles, acute angles (less than 90 degrees) and obtuse angles (greater than 90 degrees and less than 180 degrees) feel different, and different geometric shapes have different numbers of angles, such as triangles have 3 angles, squares have 4 angles, and so on.
Although tactile perception is so "intuitive", the inhabitants of the flat world still need to learn in school to use touch to supplement perception. The size of the angles, acute and obtuse, what geometric shapes they can form, etc., cannot be simply felt by touching. Touching is only a part of constructing perception.
Experienced blind people can construct in their perception what they are touching with just a little touch, while less experienced blind people need to touch more and for a longer time to know what they are touching.
In the two-dimensional world, tactile perception is considered a lower method of constructing perception, usually used by the less educated lower classes. The higher social classes need to learn another perceptual skill - visual perception.

Perceptual Skill: Visual Recognition, Fog, Light & Dark, Depth
In the middle and upper classes of the two-dimensional world, relying on touch to identify the geometric shape of others is considered "primitive" and "impolite", relying on vision to identify geometric shapes is considered elegant and appropriate. Thus, the middle and upper classes send their children to schools that teach high-level visual recognition skills to hone their offspring's eyes.
The problem is, from the perspective of the two-dimensional world, everyone sees "a line". So how do they distinguish between "a line projected by a triangle" and "a line projected by a square"? Since any geometric shape in the two-dimensional world projects "a line", how is "distinguishing recognition" possible?
The key lies in the ubiquitous fog in the two-dimensional world. With the presence of fog, distant things will look blurrier than near things, and angles will look brighter than edges. Where there is brightness (Φοίβη), there is shadow (Έρεβος).
Because of the existence of fog, different geometric shapes in the two-dimensional world project lines that are distinguishable visually. Their "depths" are different, and the images formed by the refraction of the fog to the eyes are different.
And the high colleges of the two-dimensional world teach how to construct visual perception through these differences in light and dark. Through the "projection" of one-dimensional line segments, they use the intellect (διανοια = διά + νοῦς) to restore a two-dimensional geometric shape.



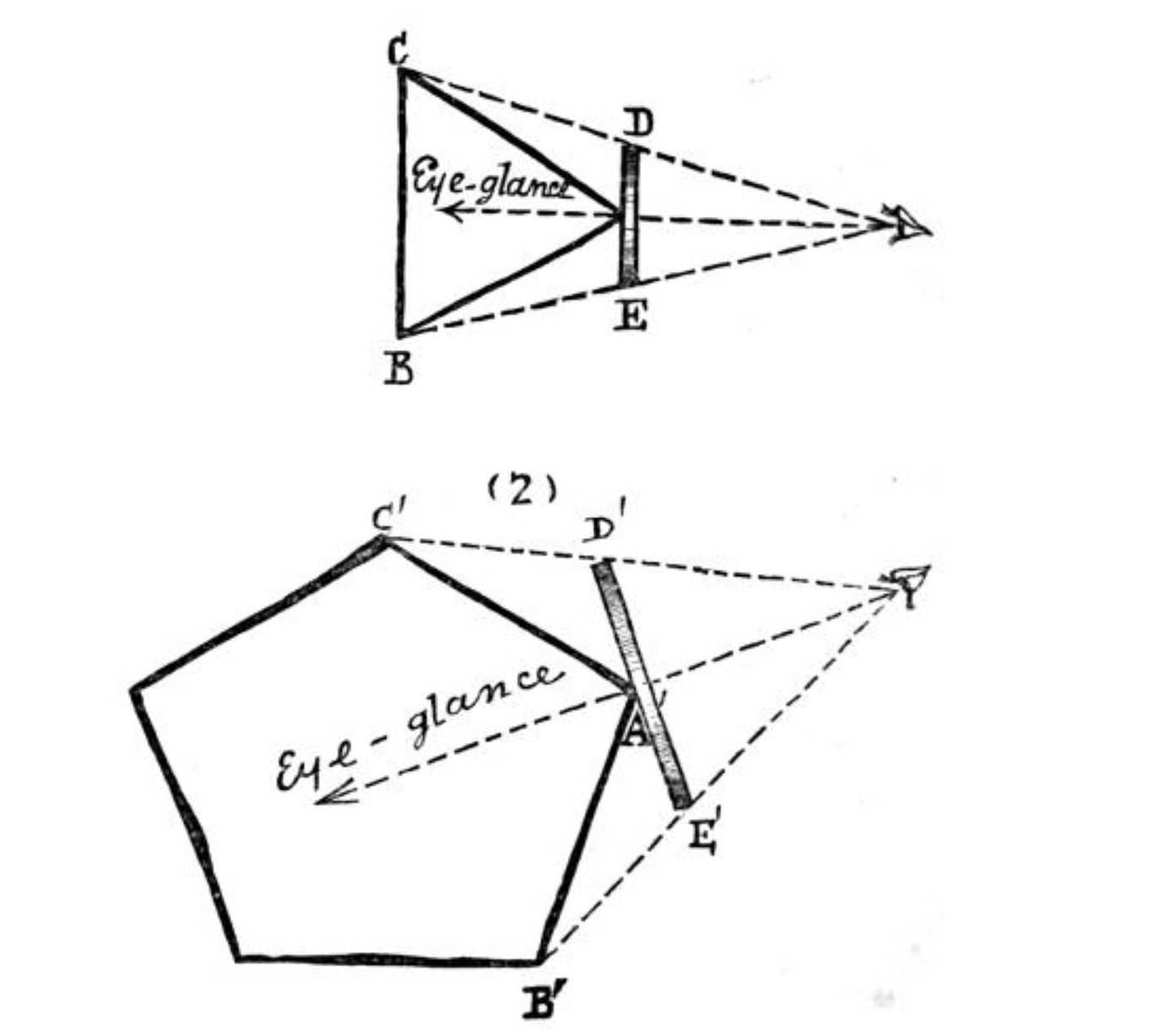
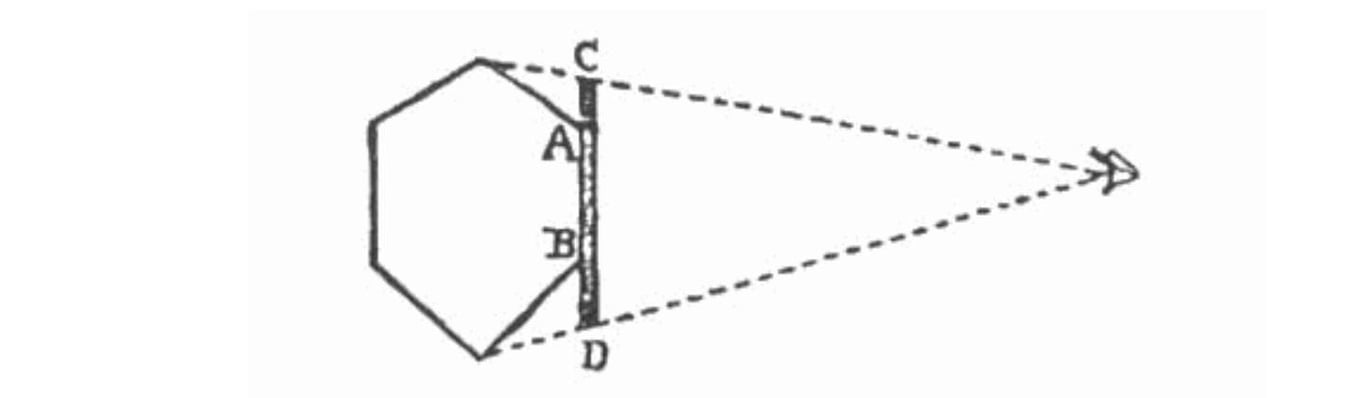
The following picture is from "Flatland", where A-Square explains how they use visual recognition to identify a geometric shape in their society.
In the picture, the eye is on the right, the dashed line is the path of the light, DE = the one-dimensional line segment projected (proportional to the image in the eye).
Due to the ubiquitous presence of fog, the angles of the geometric shape closer to the eye will appear brighter, while the angles farther from the eye will appear dimmer.
Human Vision in the Three-Dimensional World
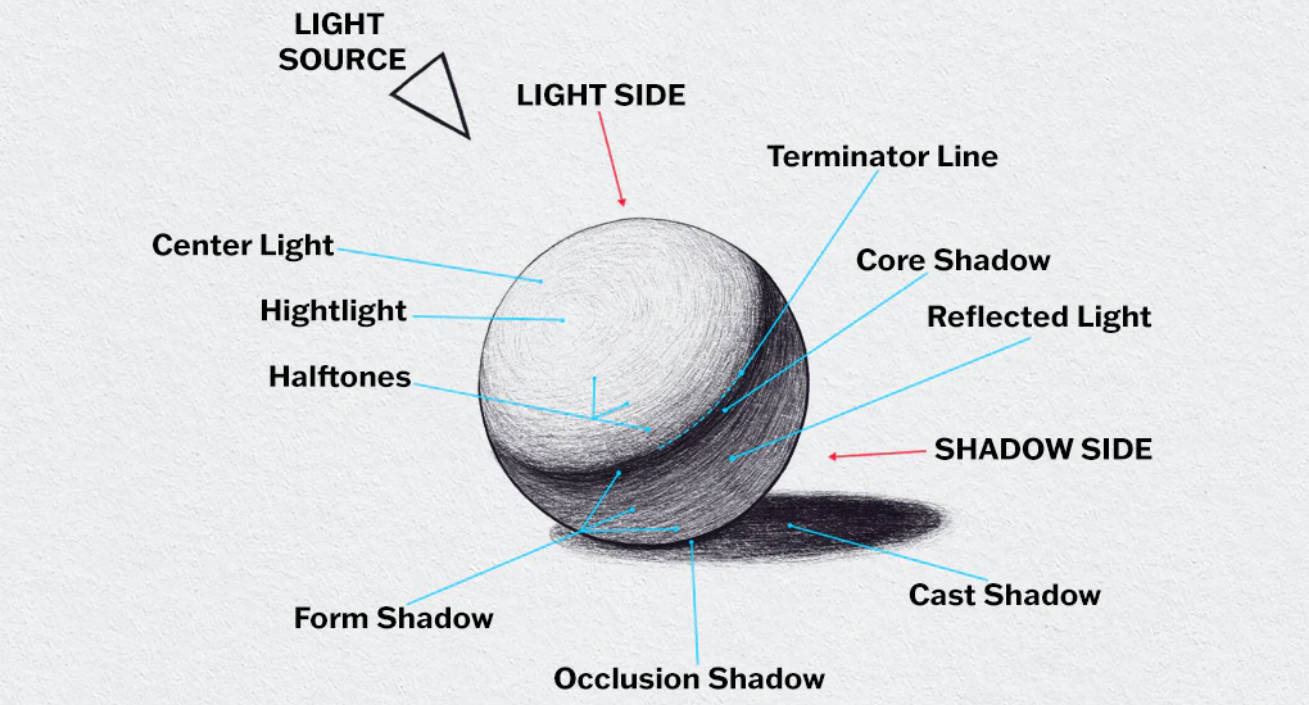
Analogous (αναλογία = ανά + λόγος) to the transformation of visual perception in the two-dimensional Flatland, what we see in the three-dimensional world is actually a two-dimensional projection of a three-dimensional object.
When we look at a painting drawn on paper, what our senses see is a two-dimensional paper, but what our perception perceives is a three-dimensional image. Where does this perceived "depth (βάθος)" come from?



The ability to "perceive" depth in a painting is related to the different painting techniques used by the artist. These techniques include:
Using "fog" to make near objects clear and far objects blurry, with more texture in near objects and less in far ones.
The difference between light and shadow, creating a sense of depth on the surface of the object.
Overlapping objects, with those in front visible and those behind partially obscured.
And so on.
Perspective & Projective Geometry
Starting from the Renaissance, painters consciously organized geometric lines and used perspective composition to make their works more approaching real and better reflect the visible geometric order of the world.
Examples of works using perspective include "The Last Supper" by Leonardo da Vinci

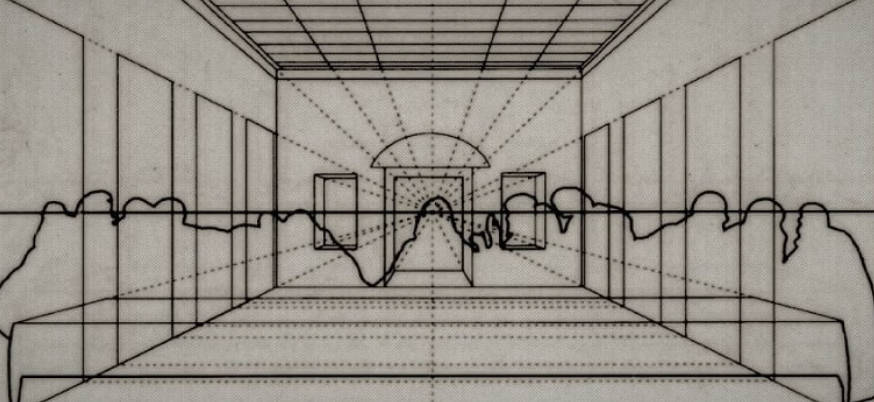
"The School of Athens" by Raphael (Raffaello Sanzio da Urbino).


In order to accurately "restore" the geometric order they could see, painters even created machines to aid in their work.
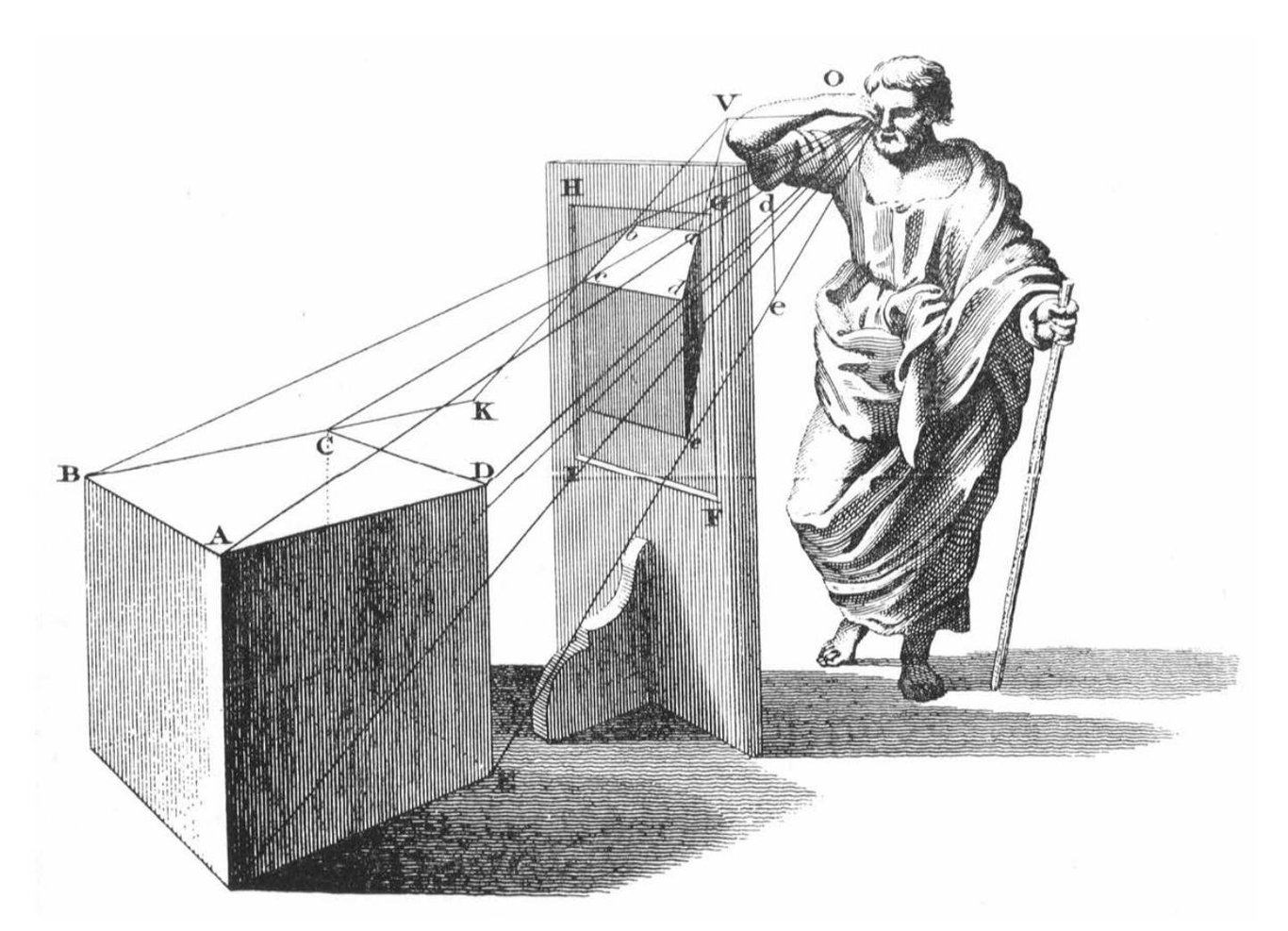


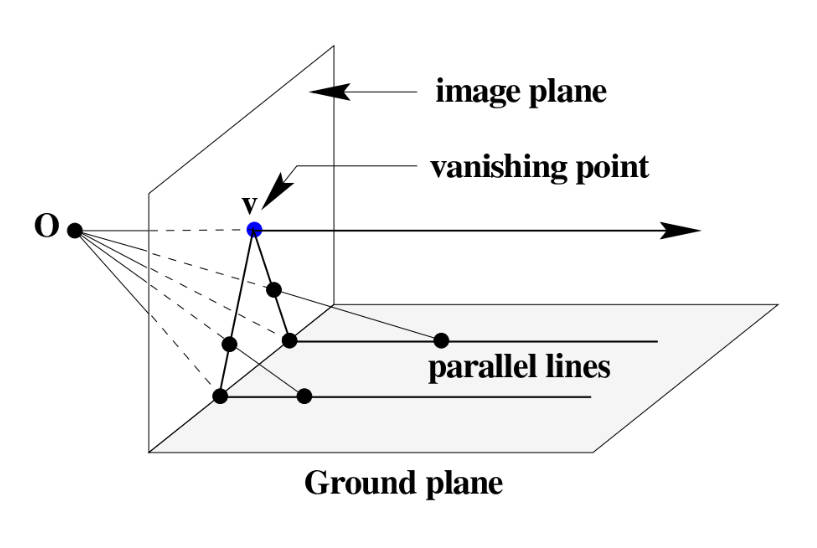
If we are directly above the ground, like a satellite observing the ground below, parallel lines will not intersect in our field of view.

When we return to the ground, we find that from our ground perspective, the parallel lines formed by the road seem to "intersect" visually at a very distant point. This point where parallel lines "intersect" at a very distant point from the ground perspective is called the vanishing point by painters.
From the ground perspective, parallel lines "intersect" at infinity.

The mathematics related to perspective drawing techniques is projective geometry.
Sensations, Perceptions, and Consciousness
In our three-dimensional world, as soon as we open our eyes, we continuously receive the "seen" two-dimensional flat images. Although the images received by the eyes are two-dimensional, our cognitive structure and acquired habits allow us to "automatically and unconsciously" transform these continuous two-dimensional flat images into three-dimensional perceptions.
At this very moment, when we look at our phones or computers, we feel that we are in a three-dimensional space. All "movements", "changes", and "time differences" occur in this three-dimensional space, but what our senses continuously see is only a two-dimensional image.
We are constantly using the visible two-dimensional plane to "deduce," "infer," "guess," and "perceive" a three-dimensional space that we experience on a daily basis.
Similar to the residents of "Flatland", A-Square's eyes can only receive "a line". It is through experience and learning that he constantly infers this "line" as "a two-dimensional figure".
Artists, by imitating this visible visual geometric order, are to some extent performing a sophisticated magic, using painting skills to make people believe that they see a three-dimensional space on a flat piece of paper.
The Possibility of Illusion
Optical illusions intentionally use people's perceptual tendencies to create confusion.













Projection as Illusion
These optical illusions unconsciously guide us from sensation to the awareness of perception, leading us to believe that the received two-dimensional plane is adequate to reconstruct the three-dimensional object, making us think that a two-dimensional image will reveal the "truth (αλήθεια)".
A two-dimensional image can "simulate (imitate)" through various means, leading people to perceive the presence of a three-dimensional object in front of them. A large painting viewed up close can create a sense of a real scene. As long as the projection's details are convincingly portrayed, people will assume that what lies behind the projection is something familiar to them.
The illusion lies in the fact that the image received by our senses certainly "exists" and that the illusory image is a "real projection." However, there is a deviation in the process of inferring from sense-certainty (sinnliche gewissheit) to perception.
This cannot be blamed on sense, because our eyes can only receive two-dimensional images. Sense-certainty (sinnliche gewissheit) has always operated in this way, only receiving a "part", "a cross-section", "a projection" of the whole being.
Perhaps the phone or computer in front of us is merely a piece of paper?
At this moment, not only does visual perception fall into illusion, but tactile perception also falls into illusion, leading us to believe that what we touch is not a piece of paper but a phone. The ears are wearing headphones, inadvertently forgetting to remove them, resulting in a perfect synchronization of the grand illusion in what is heard from nearby and afar. All these sensory stimuli are real, yet there is a significant deviation in the unconscious inference process, where the fragmented "projection" is taken as the complete whole "source," which is a component of projective geometry's work.
And one day, someone flying in a helicopter above us, observing us on the ground operating a piece of paper as if it were a phone, also becomes entangled in the great confusion of "what is this person on the ground doing."
The Hope (Ελπίς) may lie in the illusion being an incomplete projection.
The movement and rotation of the projected source will always generate subtle clues. If those who are trapped in the illusion close their eyes, not solely focusing their attention on the projection's appearance, but instead search for abnormal traces in their memories and meticulously calculate the extraordinary deviations from inertia, they might discover a glimmer of light at the exit. They could hear the loud roar of the helicopter above, prompting them to look up, where the possibility of the right angle (ορθή γωνία = right angle = correct angle) lies.

Tower of Knowledge in Two-Dimensional Projection
The wandering thoughts of the traveler shift from being fixated on the topic of perception to contemplating the depiction of the priestly hierarchy in the story of "Flatland."
In the two-dimensional plane world, polygons that closely resemble circles constitute the highest hierarchy of social order. The protagonist, A-Square, explains this.
(§ 11 Concerning our Priests),
When I call them Priests, let me not be understood as meaning no more than the term denotes with you. With us, our Priests are Administrators of all Business, Art, and Science; Directors of Trade, Commerce, Generalship, Architecture, Engineering, Education, Statesmanship, Legislature, Morality, Theology; doing nothing themselves, they are the Causes of everything worth doing, that is done by others.
These nearly circular priests are the philosophers, theologians, metaphysicians, and core rulers of the entire society. They are the aristocrats possessing the most "knowledge." They legislate and interpret the natural law (Ius naturale) based on their perceptions and strive to learn and uphold it.
Although these priests are referred to as "circles" in society, everyone knows that no "circle" is truly a "circle"; all "circles" are merely approximations of polygons (300 polygons, 400 polygons, 500 polygons, and so on).

Doctrine of Two-Dimensional Projection: Attend to your Configuration
The priests' comprehension of metaphysics (μεταφυσική = μετά + φυσική = beyond physics) and natural law (ius naturale) is transformed and popularized into the doctrines, laws, culture, customs, and all the subtle thoughts and actions of the general public.
The core doctrine of the social order in the two-dimensional world where A-Square resides is that
(§ 12 Of the Doctrine of our Priests)
As to the doctrine of the Circles it may briefly be summed up in a single maxim, “Attend to your Configuration.” Whether political, ecclesiastical, or moral, all their teaching has for its object the improvement of individual and collective Configuration—with special reference of course to the Configuration of the Circles, to which all other objects are subordinated.
That is to say, the highest value in A-Square's society is to strive towards resembling a "Circle" in geometric figures. The regular polygons with a greater number of sides bear a closer resemblance to a "circle". Consequently, a polygon with 12 sides is considered more noble than one with 10 sides, and a polygon with 10 sides is deemed more noble than one with 5 sides.
The foundation of society is constituted by triangles with 3 sides. These triangles are further divided into equilateral triangles, which bear a stronger resemblance to circles, isosceles triangles at the next level, while other types of triangles are viewed as inferior.

"Round-based and Attend to your Configuration" is the core value and worldview of the society in which A Square resides. It serves as the foundation for the entire political order.
There was once a famous philosopher in the two-dimensional plane world. His name was Pantocyclus (panto + cyclus = everywhere is round). The metaphysics of this philosopher can be summarized as,
(§ 12 Of the Doctrine of our Priests)
All faults or defects, from the slightest misconduct to the most flagitious crime, Pantocyclus attributed to some deviation from perfect Regularity in the bodily figure, caused perhaps (if not congenital) by some collision in a crowd; by neglect to take exercise, or by taking too much of it; or even by a sudden change of temperature, resulting in a shrinkage or expansion in some too susceptible part of the frame. Therefore, concluded that illustrious Philosopher, neither good conduct nor bad conduct is a fit subject, in any sober estimation, for either praise or blame. For why should you praise, for example, the integrity of a Square who faithfully defends the interests of his client, when you ought in reality rather to admire the exact precision of his right angles? Or again, why blame a lying, thievish Isosceles, when you ought rather to deplore the incurable inequality of his sides?
What the entire society prioritizes the most is the notion of "tending to be round". The value system heavily centers around geometric figures, while placing less emphasis on intangible virtues (ἀρετή) such as temperance (σωφροσύνη), courage (ἀνδρεία), justice (δικαιοσύνη), wisdom (σοφία), and so forth.
In the society where A-Square resides, the perception of nobility and beauty (καλός) revolves solely around the concept of "tending to be round".
The society operates in accordance with this order, and it has been functioning since the beginning of time, spanning two millennia (the events in "Flatland" revolve around the past 1999 and the approaching new millennium of 2000).
Certainly, the doctrine of "Round-based and Attend to your Configuration" occasionally faces challenges when it comes to interpreting reality.
(§ 12 Of the Doctrine of our Priests)
Theoretically, this doctrine is unquestionable; but it has practical drawbacks. In dealing with an Isosceles, if a rascal pleads that he cannot help stealing because of his unevenness, you reply that for that very reason, because he cannot help being a nuisance to his neighbours, you, the Magistrate, cannot help sentencing him to be consumed—and there’s an end of the matter. But in little domestic difficulties, when the penalty of consumption, or death, is out of the question, this theory of Configuration sometimes comes in awkwardly; and I must confess that occasionally when one of my own Hexagonal Grandsons pleads as an excuse for his disobedience that a sudden change of temperature has been too much for his Perimeter, and that I ought to lay the blame not on him but on his Configuration, which can only be strengthened by abundance of the choicest sweetmeats, I neither see my way logically to reject, nor practically to accept, his conclusions.
A-Square also observed that the upper echelons of his society did not strictly adhere to the most rigid doctrines when it came to educating their children.
(§ 12 Of the Doctrine of our Priests)
For my own part, I find it best to assume that a good sound scolding or castigation has some latent and strengthening influence on my Grandson’s Configuration; though I own that I have no grounds for thinking so. At all events I am not alone in my way of extricating myself from this dilemma; for I find that many of the highest Circles, sitting as Judges in law courts, use praise and blame towards Regular and Irregular Figures; and in their homes I know by experience that, when scolding their children, they speak about “right” and “wrong” as vehemently and passionately as if they believe that these names represented real existence, and that a human Figure is really capable of choosing between them.
In A-Square's society, 300 years ago, the ruling priests held the belief that women lacked rationality, leading them to prohibit women from receiving education.
One other word of warning suggest itself to me, though I cannot so easily mention a remedy; and this also refers to our relations with Women. About three hundred years ago, it was decreed by the Chief Circle that, since women are deficient in Reason but abundant in Emotion, they ought no longer to be treated as rational, nor receive any mental education. The consequence was that they were no longer taught to read, nor even to master Arithmetic enough to enable them to count the angles of their husband or children; and hence they sensibly declined during each generation in intellectual power. And this system of female non-education or quietism still prevails.
And A-Square is concerned that this would lead to the overall decline of society. In comparison to 300 years ago, the intelligence of the contemporary residents in the two-dimensional world is gradually diminishing. A-Square firmly believes that it is imperative for the higher authorities to once again permit women to receive education.
Already methinks I discern a weakness in the grasp of mathematical truth at the present time as compared with the more robust intellect of our ancestors three hundred years ago. I say nothing of the possible danger if a Woman should ever surreptitiously learn to read and convey to her Sex the result of her perusal of a single popular volume; nor of the possibility that the indiscretion or disobedience of some infant Male might reveal to a Mother the secrets of the logical dialect. On the simple ground of the enfeebling of the male intellect, I rest this humble appeal to the highest Authorities to reconsider the regulations of Female education.
A-Square's perspective is still constrained by the inertia of his deeply ingrained worldview.

Powerful Opponents of the Two-Dimensional Configuation Order
The order established by the Circle Priest class, with its emphasis on "Attend to your Configuration", has encountered formidable challengers in the history of the two-dimensional world.
In the past, people have discovered that the recognition of geometric shapes can be differentiated by coloring various edges.

(§ 9 Of the Universal Colour Bill)
Year by year the Soldiers and Artisans began more vehemently to assert—and with increasing truth—that there was no great difference between them and the very highest class of Polygons, now that they were raised to an equality with the latter, and enabled to grapple with all the difficulties and solve all the problems of life, whether Statical or Kinetical, by the simple process of Colour Recognition. Not content with the natural neglect into which Sight Recognition was falling, they began boldly to demand the legal prohibition of all “monopolizing and aristocratic Arts” and the consequent abolition of all endowments for the studies of Sight Recognition, Mathematics, and Feeling. Soon, they began to insist that inasmuch as Colour, which was a second Nature, had destroyed the need of aristocratic distinctions, the Law should follow in the same path, and that henceforth all individuals and all classes should be recognized as absolutely equal and entitled to equal rights.
These revolutionaries are known as "Chromatistes."
The "Chromatistes" launched a formidable challenge against the "Formalist Order".
The "Chromatistes" put forth a new metaphysics and value system - "Color solves everything, and the spectrum signifies fulfillment."
However, the implementation of the "Chromatistes Values" (Colorist Values) resulted in unexpected side effects.
Science and Art were deemed redundant, leading to a decline in the overall intellect of society.
(§ 9 Of the Universal Colour Bill)
The Art of Sight Recognition, being no longer needed, was no longer practised; and the studies of Geometry, Statics, Kinetics, and other kindred subjects, came soon to be considered superfluous, and fell into disrespect and neglect even at our University. The inferior Art of Feeling speedily experienced the same fate at our Elementary Schools. Then the Isosceles classes, asserting that the Specimens were no longer used nor needed, and refusing to pay the customary tribute from the Criminal classes to the service of Education, waxed daily more numerous and more insolent on the strength of their immunity from the old burden which had formerly exercised the twofold wholesome effect of at once taming their brutal nature and thinning their excessive numbers.

It has also caused unexpected confusion - confusion between circles and lines.
(§ 9 Of the Universal Colour Bill)
Bear in mind the decay of Sight Recognition which threatened society at the time of the Colour revolt; add too the certainty that Woman would speedily learn to shade off their extremities so as to imitate the Circles; it must then be surely obvious to you, my dear Reader, that the Colour Bill placed us under a great danger of confounding a Priest with a young
Woman.
The original intention of "Chromatism" was to weaken the aristocratic class, but inadvertently made the aristocratic class even stronger (due to the preservation of intellect).
The second object aimed at by the Bill was the gradual demoralization of the Circles themselves. In the general intellectual decay they still preserved their pristine clearness and strength of understanding. From their earliest childhood, familiarized in their Circular households with the total absence of Colour, the Nobles alone preserved the Sacred Art of Sight Recognition, with all the advantages that result from that admirable training of the intellect. Hence, up to the date of the introduction of the Universal Colour Bill, the Circles had not only held their own, but even increased their lead of the other classes by abstinence from the popular fashion.

Under the belief that "color can solve everything," people also discovered the use of color for deception because, in the new system, people solely relied on color.
(§ 9 Of the Universal Colour Bill)
It happened that an Isosceles of a low type, with a brain little if at all above four degrees—accidentally dabbling in the colours of some Tradesman whose shop he had plundered—painted himself, or caused himself to be painted (for the story varies) with the twelve colours of a Dodecagon. Going into the Market Place he accosted in a feigned voice a maiden, the orphan daughter of a noble Polygon, whose affection in former days he had sought in vain; and by a series of deceptions—aided, on the one side, by a string of lucky accidents too long to relate, and, on the other, by an almost inconceivable fatuity and neglect of ordinary precautions on the part of the relations of the bride—he succeeded in consummating the marriage. The unhappy girl committed suicide on discovering the fraud to which she had been subjected.
The struggle between "chromatism (coluorism)" and "formalism" ended in a bloody coup and civil war, with the intellectually dominant old priesthood using means to eliminate the "Chromatistes."

After that, colors were prohibited nationwide.
A-Square heard that colours would only appear in some of the most advanced and profound courses.
(§ 10 Of the Suppression of the Chromatic Sedition)
Needless to say that henceforth the use of Colour was abolished, and its possession prohibited. Even the utterance of any word denoting Colour, except by the Circles or by qualified scientific teachers, was punished by a severe penalty. Only at our University in some of the very highest and most esoteric classes—which I myself have never been privileged to attend—it is understood that the sparing use of Colour is still sanctioned for the purpose of illustrating some of the deeper problems of mathematics. But of this I can only speak from hearsay.
The secret of colours was passed down in a cruel manner at the highest level.
Elsewhere in Flatland, Colour is now non-existent. The art of making it is known to only one living person, the Chief Circle for the time being; and by him it is handed down on his death-bed to none but his Successor. One manufactory alone produces it; and, lest the secret should be betrayed, the Workmen are annually consumed, and fresh ones introduced. So great is the terror with which even now our Aristocracy looks back to the far-distant days of the agitation for the Universal Colour Bill.

