槓桿ETF的報酬和風險

★★★★★
狂徒Cover (13500字,35分鐘。)
本篇不適合「無基礎」的創作者和讀者,請留意。
有些投資圈作者說我的教學系列文章太硬,所以我警告先放前面。
好吧,這是你能找到最專業的中文槓桿ETF「介紹」,但是看完會對槓桿ETF有更充足的知識,也能理解我喜歡毀滅信仰的信仰。
身處M型化的知識斷層就是這樣,我寫的文章在坊間沒什麼人懂,但看得懂、知道我哪裡寫錯的學界和業界人士又喜歡潛水。
目中無人,是因為根本找不到人。
狂徒風格文章的好處是別人無法抄襲,壞處就是很無聊。
所以如果有寫錯,歡迎各位踢館,我獨孤求嗆 :)
1. 槓桿ETF和「指數投資」圈
指數投資作者,不論是主流族群、基本教義信徒或是興風作浪派,大多會提到指數ETF.
結果就是,只要某家ETF和指數稍微有關,就會有民眾拿去問作者,然後一些議題就被「走私」進指數圈。
例如,有人好奇short put和covered call的差異,看起來payoff明明一樣。
這是很純粹的選擇權領域問題,一般指數作者不知道,也不必知道。
可是如果有人問指數作者,「XYLD和一般SP500指數ETF有什麼差異?」,老師就尷尬了。
他不能拒絕回答,又無法說清楚,所以最後只能針對投資心態和手續/內扣費這些邊緣議題下手。
同樣的,槓桿ETF原理簡直是「包著糖衣的核彈」。
一樣是ETF,一樣長期持有,一樣追蹤大盤指數,一樣不選股、不擇時、不看新聞.....那槓桿ETF和原型ETF有什麼不同? 槓桿ETF的價格怎麼變化? 槓桿ETF適合長期持有嗎? 槓桿ETF是不是投機專屬標的?
你以為你問了很簡單的問題,結果不小心把老師炸成灰。
負責任的作者,會承認自己「不知道」的部分,然後建議讀者考慮漲跌風險、心理因素和商品細節,再自行決定。
他們不怕被嘲笑,而是站在讀者的立場提供建議,所以我一向禮遇這類創作者。
至於另外一群不懂又愛亂講的,剛好符合我的「狩獵」嗜好,就有機會被我diss。
根據我的觀察和交流,由於「單日槓桿」原理涉及的知識,遠超坊間作者能吸收的正常範疇,所以如果妳真的有興趣,問圈外人反而會比較妥當。
當然,如果你想深入討論槓桿ETF,包括工具層面之外的因素,也可以找下面幾個人。
加入我的Discord
https://discord.com/invite/kJRVXf8ENc
找「淺談保險觀念」的PTT正二王(林大仁)
或是找PTT多拉王(張先生, ffaarr)
雖然這些人和我的意見有時不同甚至「相反」,但是因為有給夠廣告費......
說錯了,因為客觀理性,知識體系較完整,願意研究和查詢資料,我認為他們的文章對讀者有幫助。
2. 追蹤基準和實際表現
槓桿ETF的目標是「扣除費用前,單日報酬達到追蹤基準的特定倍率」。
所以每日的實際報酬,即為基準報酬×倍率-費用。
例如0050,基準是台灣前50大上市公司的市值加權平均指數(約略等於大盤),倍率為1.0
所以投資人每天實際的報酬變化,可以直接當成大盤報酬減掉ETF成本。
同理,0050正2(00631L)的報酬,大概是每天雙倍大盤報酬減掉ETF成本。
0050反1(00632R),是負一倍大盤報酬減掉ETF成本。
(元大,是不是該意思一下? 不然我下次就講006208了。)
因此,當我們提到長期持有槓桿ETF的「偏離」,其實同時隱含四個概念。
第一是必要成本,例如指數授權費、保管費、經理費等。
這種成本只會減少報酬,不過變動較小。
第二種是追蹤誤差,可能發生在指數公司或投信身上,例如折溢價。
換句話說,複製指數表現之後,可能是賺或賠。
不過實務上,由於投信或基金公司會算出總內扣費用,所以前面兩種概念可以合併起來,當作操作層面的成本。
第三種,是槓桿倍率造成的偏離。
只要原始指數有所變化,槓桿指數就會把報酬等比例縮放。
第四種,才是造成槓桿ETF充滿神秘感的「主因」,來自於指數編寫規則。
有人稱為波動率衰退或槓桿耗損,也有人(例如Vocus海貓貓)稱為無中生有,我比較喜歡用「波動曝露」來形容。
這些因素都會影響投資人報酬,而且性質會和參照基準相關。
舉個例子,某段時間0050下跌21.0%,50正2下跌33.5%
如果用單純的指數當參考,那麼50正2跑輸大盤12.5%
如果把槓桿倍率考慮進去,那麼50正2跑贏雙倍大盤8.5%
至於「槓桿前報酬」能不能當報酬,據說是坊間指數基本教義派和業界人士的吵架八卦,單純是腦容量不夠,可惜兩邊我都不熟,就不展開了。
接下來切入技術細節,我會談到兩個價格機制版本。
一個比較硬,適合投資人;另一個比較好懂,適合路人。
3. Riemann, Brown, Taylor, & Ito
小學老師推導圓形面積,會先把圓形切成小的扇形,然後拼成一個類長方形。
只要分割越細,圓面積就會越接近長方形面積,也就是 r×πr=πr²
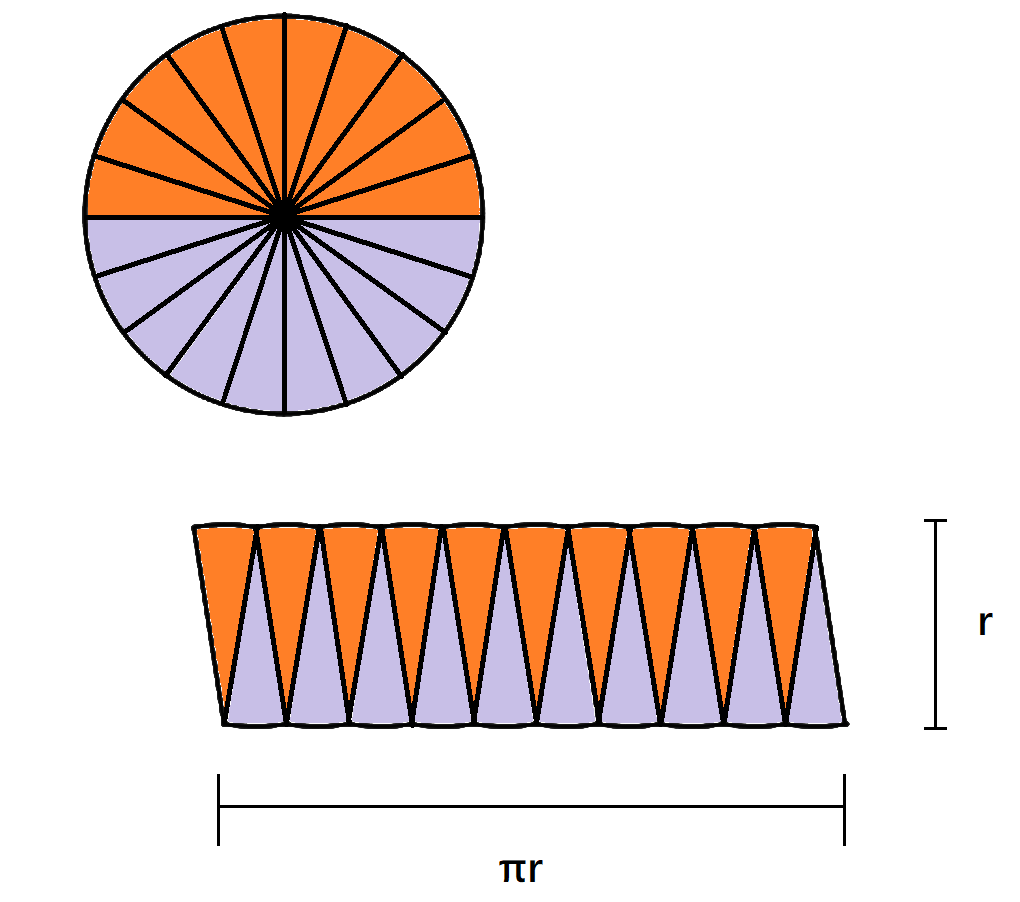
不管怎麼切,圓形面積都不會改變,所以我們只要往「切成最細」的方向前進,就能得到答案。
而不只圓型,人類對於許多函數都採用「先切割再合併」的方式,用數學的語言來說,先定義微分再定義積分。
可是在股價變化上,我們發現此路不通。
從年線到tick, 不管如何放大,股價都不「平滑」,越切下去就有越多新資訊跑出來。
換句話說,一般微積分派不上用場。
為了描述股價變化,人們使用機率函數,想辦法繞過這些限制。
回想一下中學時期的積分,叫做「黎曼積分」,它可以用來處理「有界變分」的函數。
我在〈來吧選擇權,Black-Scholes 模型〉中也提過,股票價格走勢和幾何布朗運動(GBM)有相近的性質,包括該泛函的「二次變分非零」,以及連續而一階不可微分。
既然幾何布朗運動並不是有界變分,我們無法用黎曼積分定義出隨機積分。
因此相反的,我要先定義出隨機積分,再回頭找微分。
隨機微積分是一個重要且龐大的領域,不過我們目前只會用到簡單的概念來建模。
如果讀者有興趣繼續研究,可以找一些書,例如"Stochastic Differential Equations"或之前我推過的《計量財務金融》(韓傳祥)。
4. Ito性質和基本原理
言歸正傳,我們先看熟悉的微分。
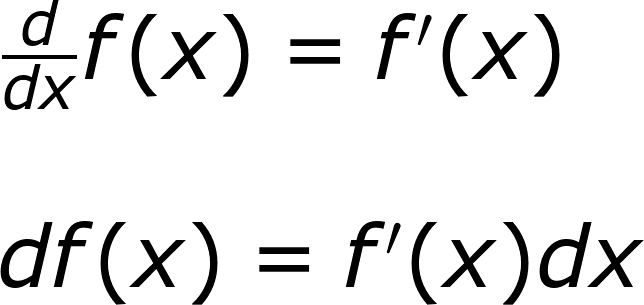
可是對於布朗運動(維那過程)而言,沒辦法直接找出微分,所以我要借用泰勒展開。
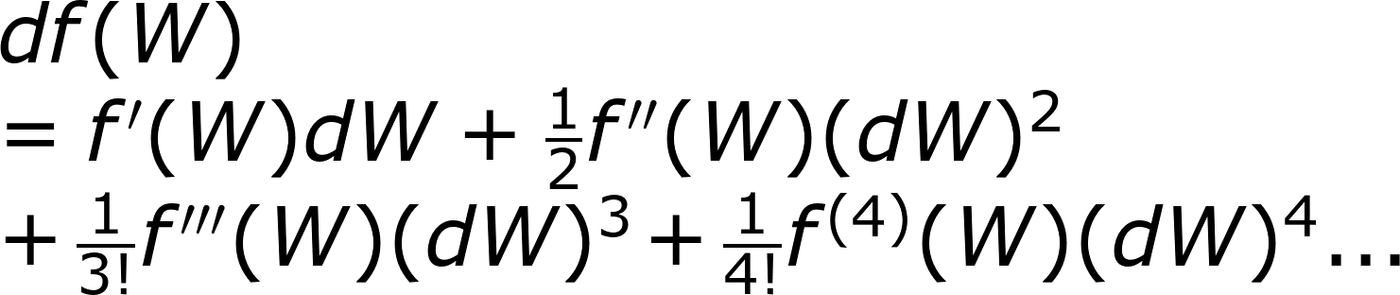
我們知道二階不為零,而且其值 (dW)²=dt
二階之後皆可忽略,因此
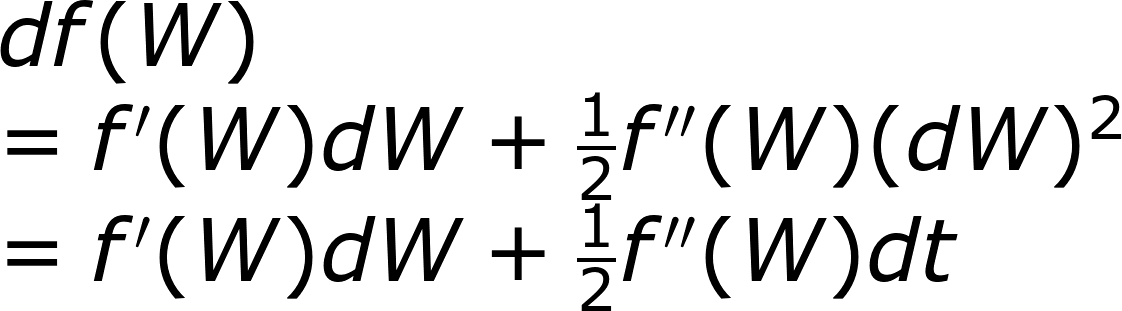
這串公式也屬於 Ito Lemma
5. 價格變化
現在,我們用隨機微分方程建模,並描述價格變化。
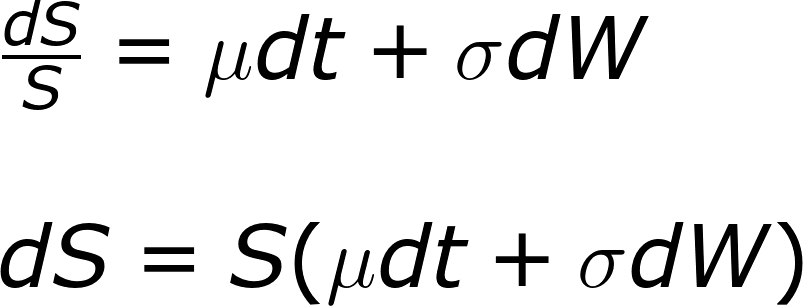
S: 價格
μ: 飄移(預期報酬)
σ: 波動
W: 布朗運動(Wiener)
至於槓桿產品,我們可以想成借錢投資。
借錢的利率是r,借錢總額是槓桿倍率B減一,然後整組商品的內扣通稱為f.
因此,瞬間的槓桿報酬率,會是原指數的B倍再扣掉一些成本。
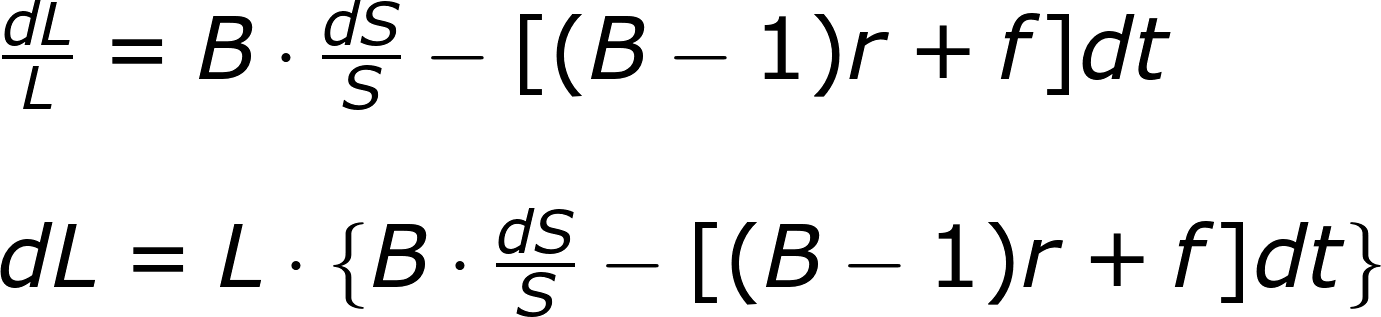
r: 借款利率
f: ETF內扣費
B: 槓桿率
話分兩頭
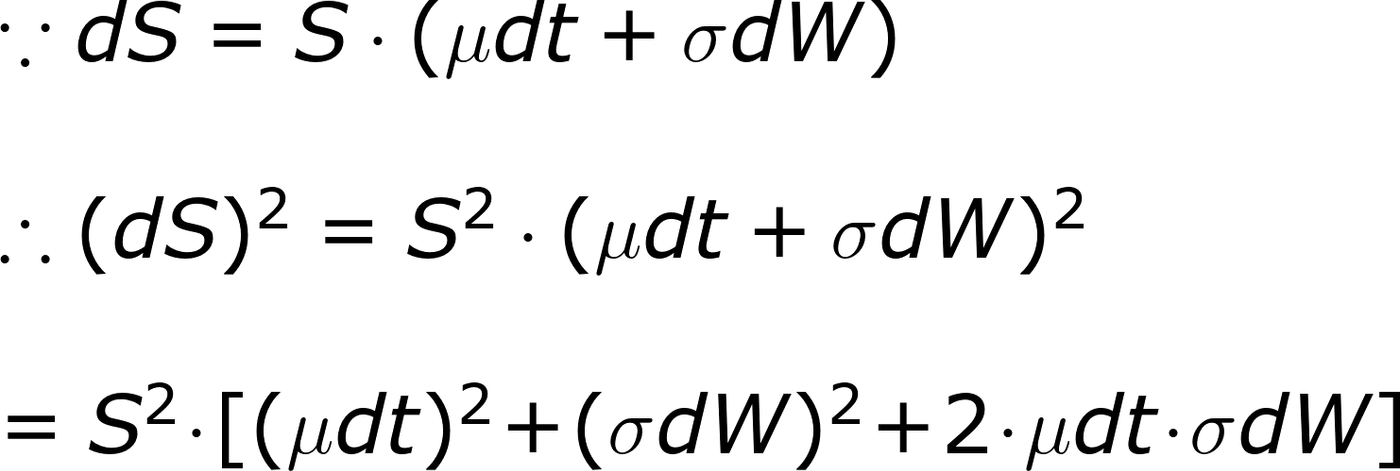
其中涉及dt²和dtdW的項目可以丟掉,但唯獨(dW)²不可丟。
dt²=0好理解,而dtdW因為是個平賭(martingale/鞅/馬丁格爾)又不飄移,所以也是零。
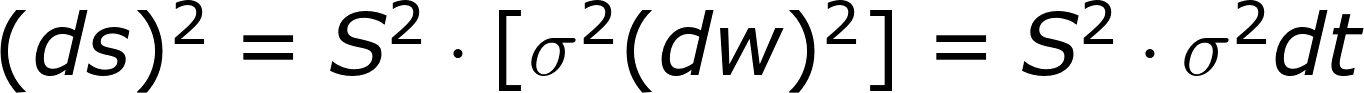
所以(ds)²=S² σ²(dw)²=S² σ² dt
相似的
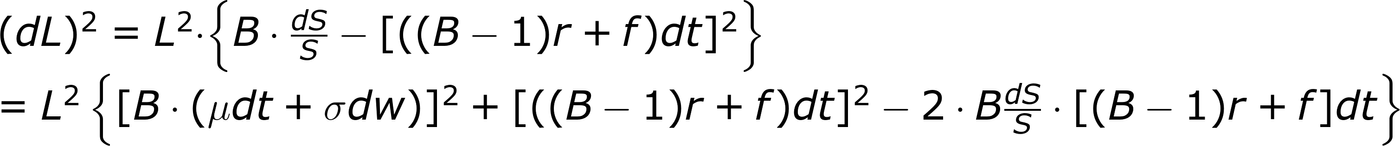
同樣的,dt²和dtdW項目可以直接歸零。
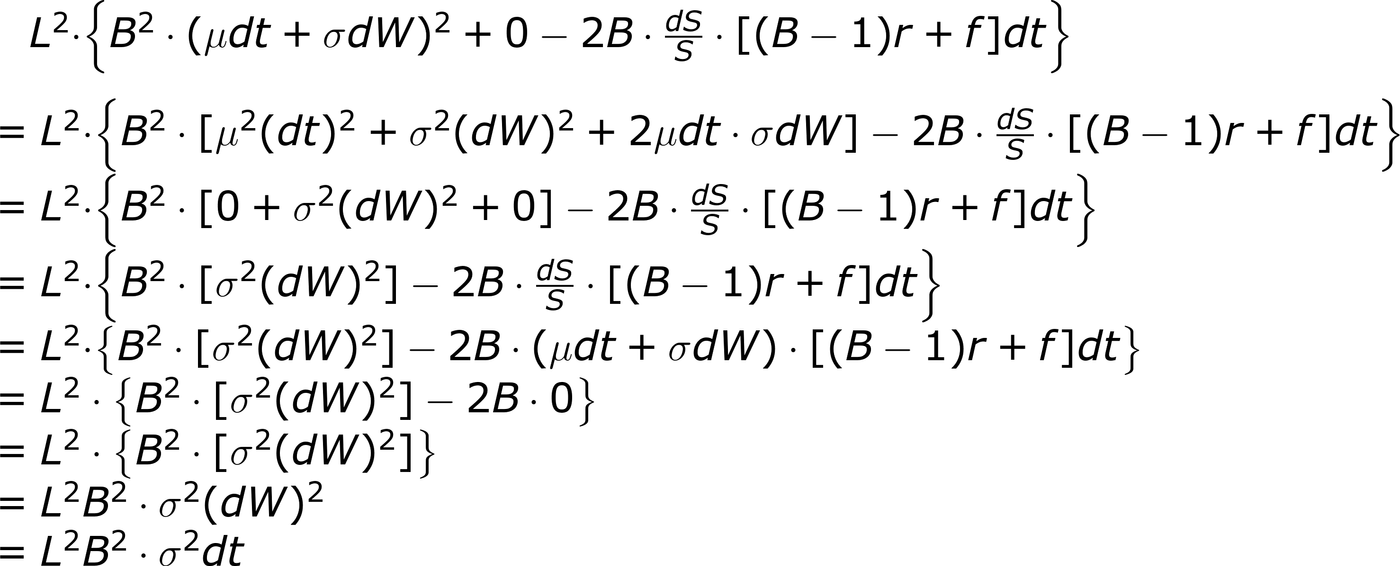
現在,來看指數價格自然對數的部分,一樣採用Taylor series的形式,(dS)²的推導在上文。
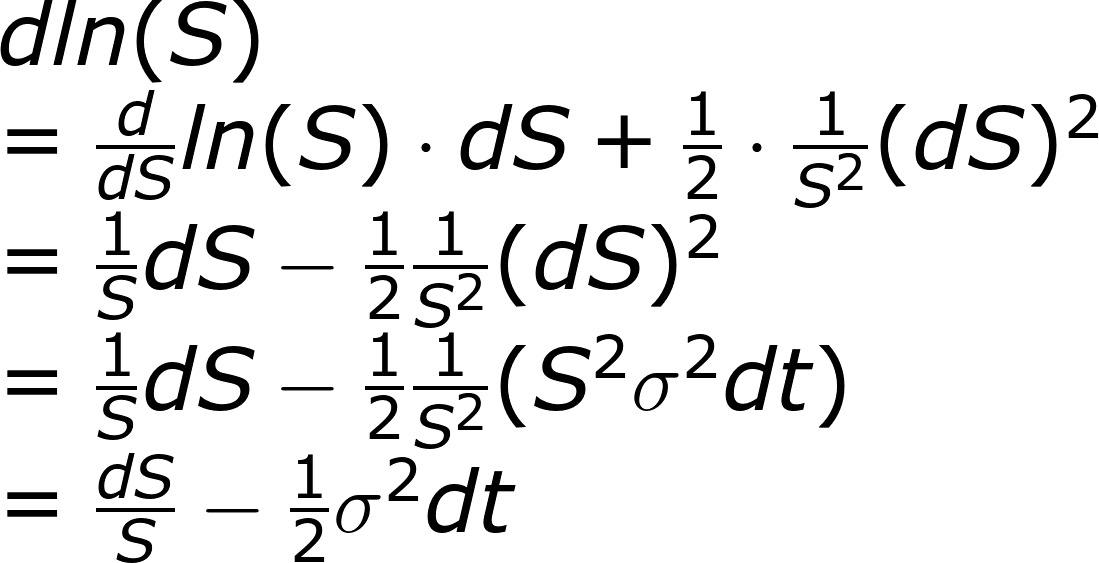
再用同樣的方式,處理槓桿商品的價格,這次需要注意(dL)²
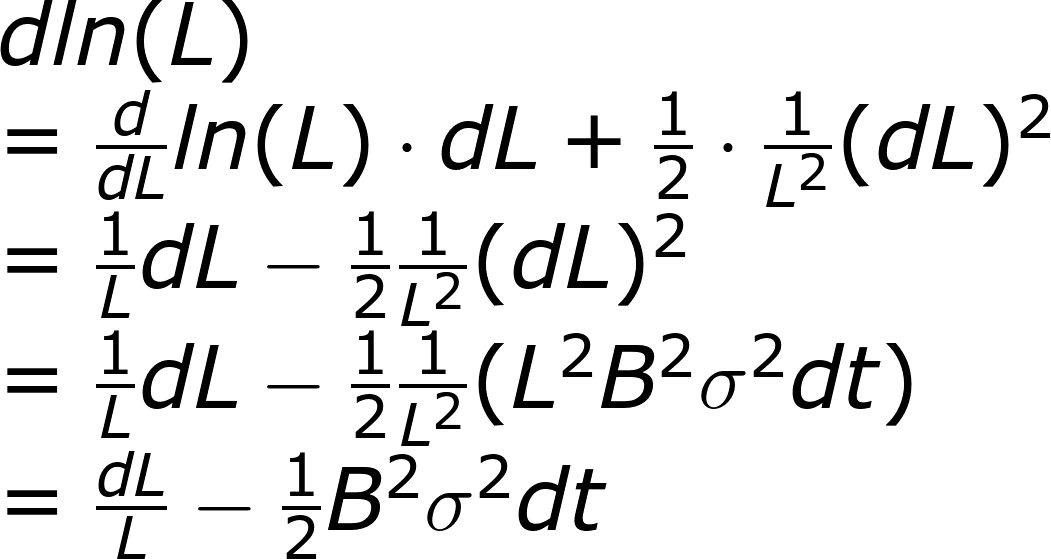
這時把dL帶入
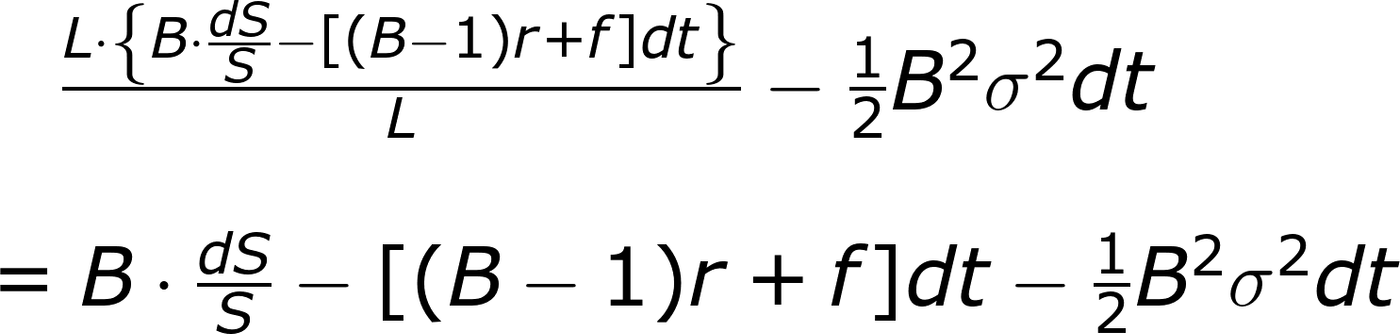
就像我們在BS公式中的做法,現在要把隨機的S項消滅掉。
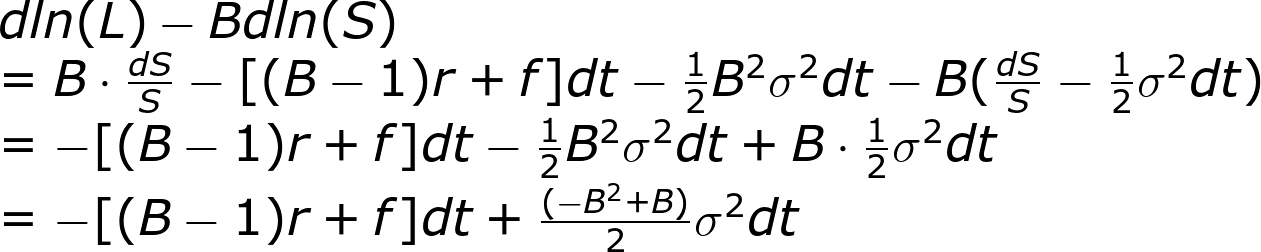
我們處理L,並裝上積分。
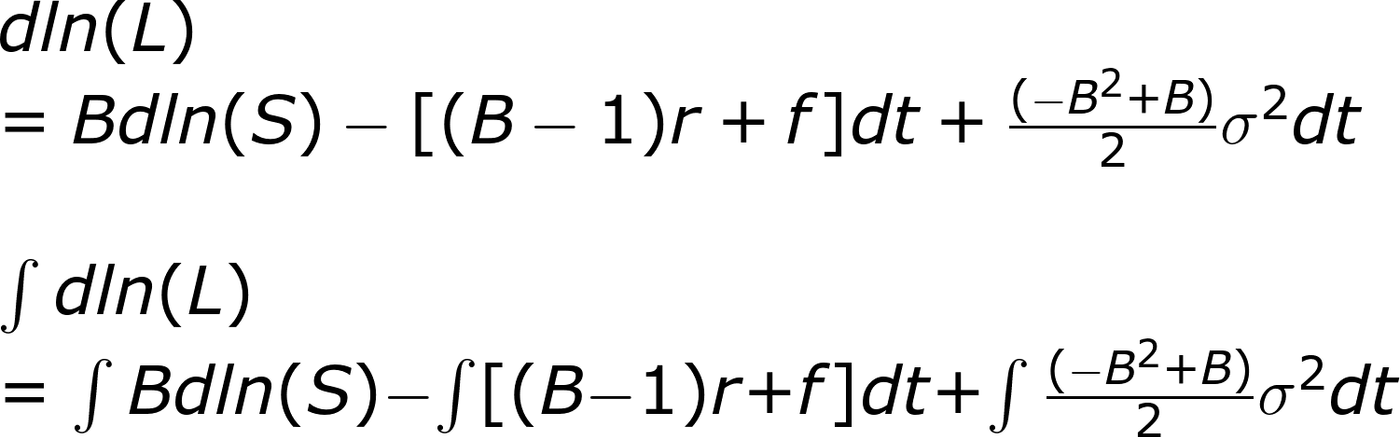
別忘了
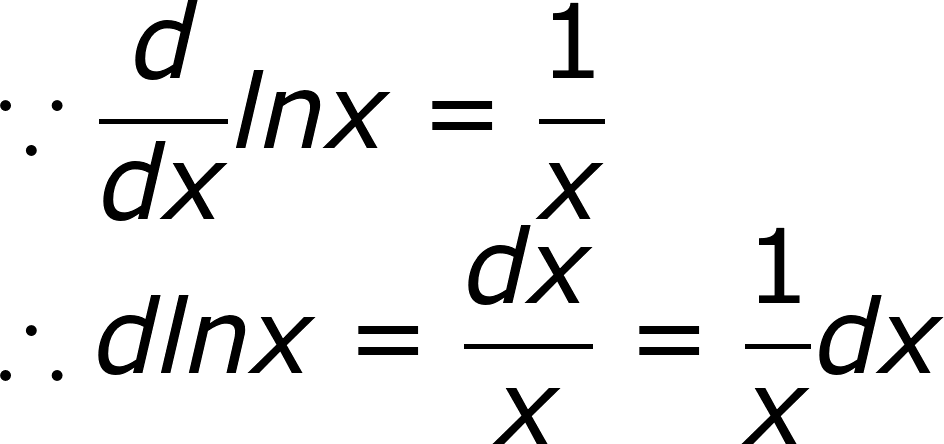
把上面的積分換元
其中C是常數項
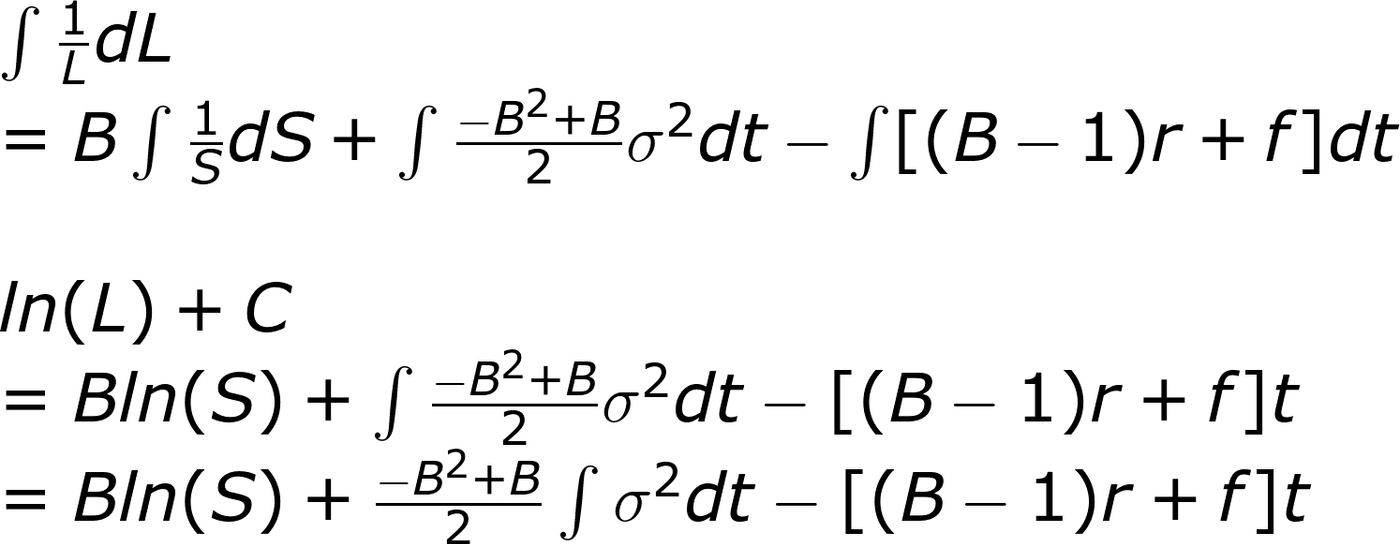
為了得到L的報酬,以e為對數底
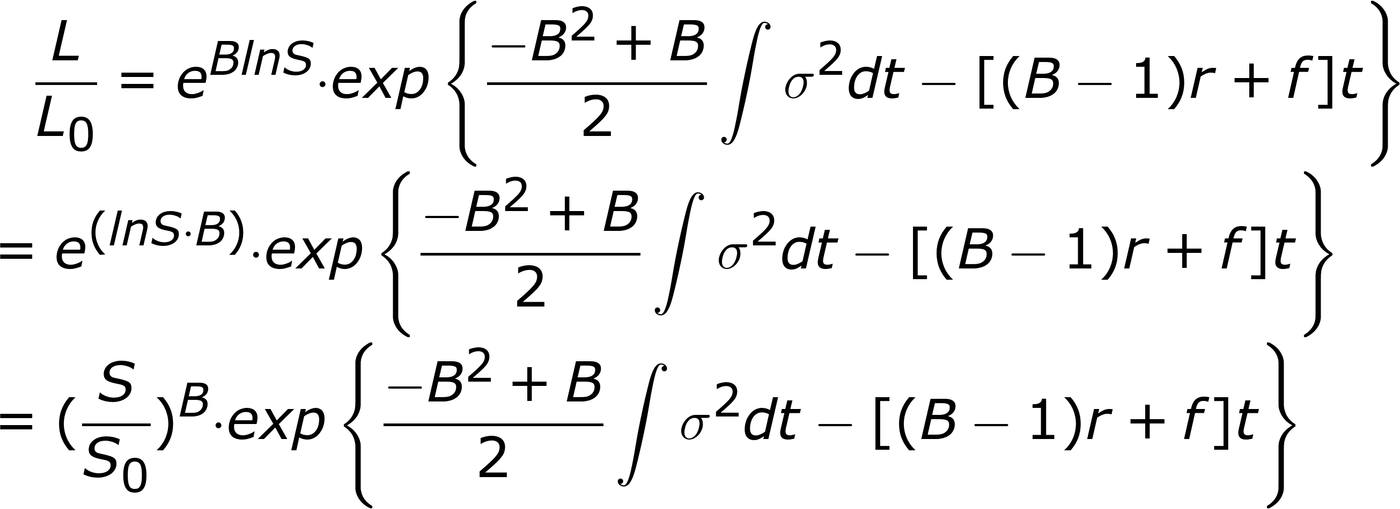
這就是LETF的長期報酬。
如果我們假設波動率固定,可以進一步簡化,直接用波動率取代波動對時間的定積分。
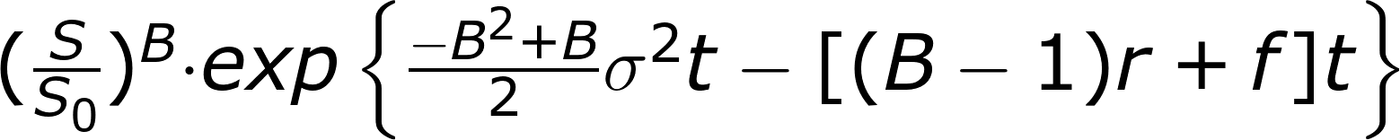
換另外一種表現形式,我們可以將槓桿商品的價格變化整理得更簡潔。
本來是我和作者們私下「吵架」的簡述,現在公開。

6. 最佳槓桿率
為了找處最佳槓桿倍率,我們直接對ln(L)微分。
如果偏微分的結果是0,代表此處有極值。
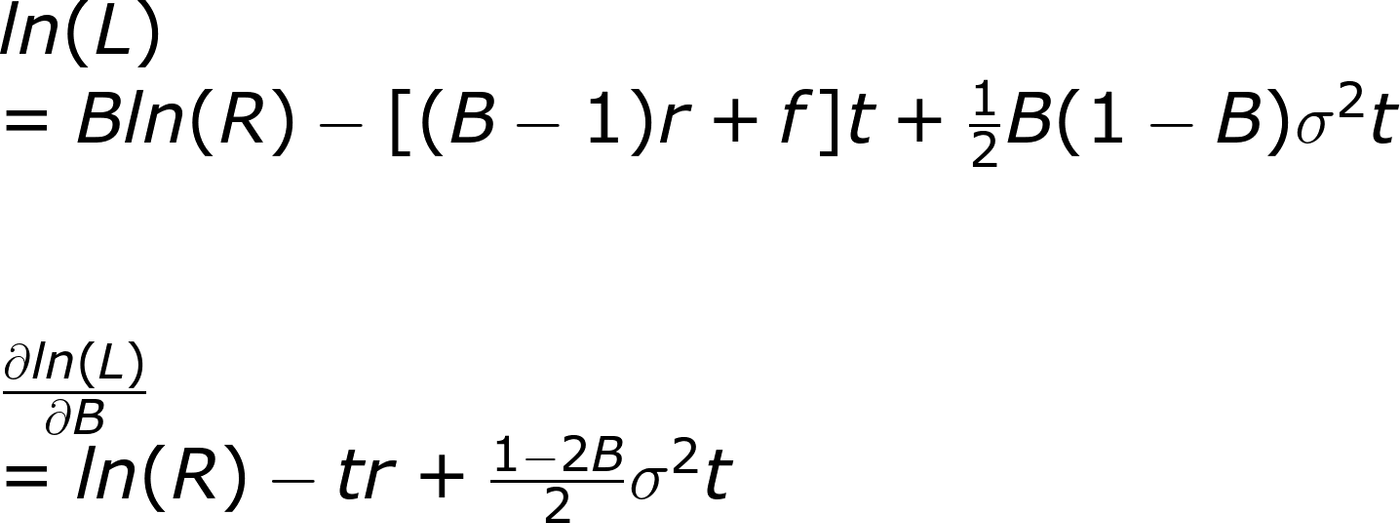
偏微分的值要剛好是0,我們可以找出這時的B
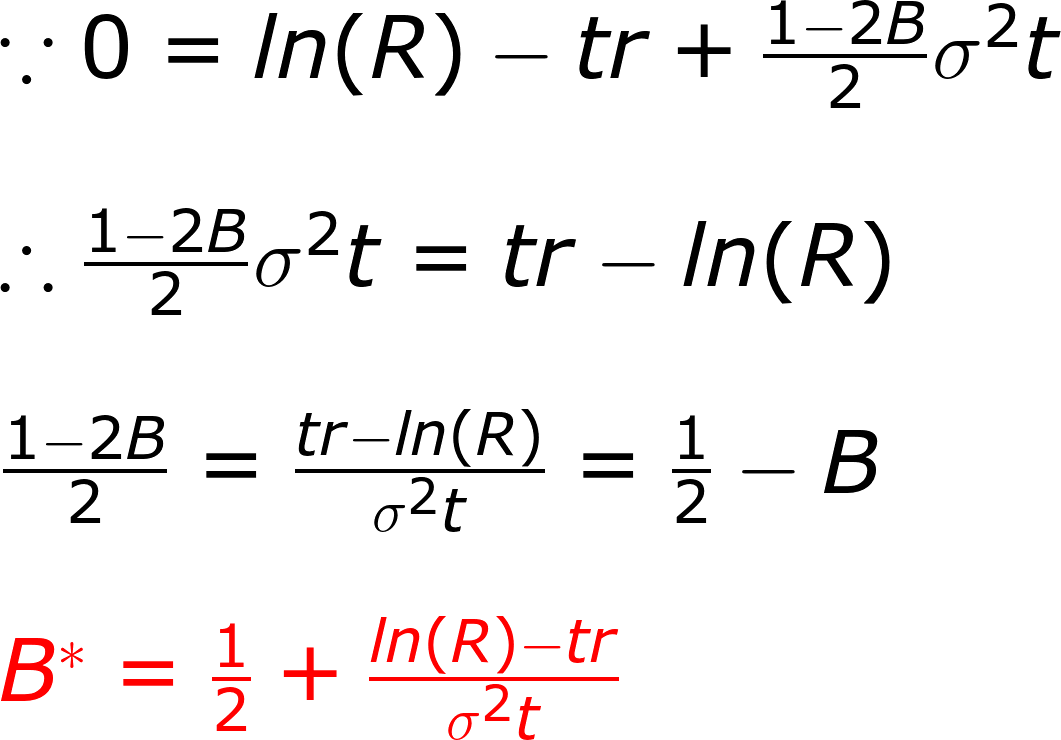
這就是最佳槓桿率,呼應我在〈槓桿ETF適合長期持有嗎?〉一文的結論。
此處的極值不受費率影響,但會受到貸款利率和時間影響。
7. 「狂徒,有沒有比較簡單的版本?」
我寫過,當槓桿率為μ/σ²,總報酬會最高,這是近似的「概算」。
如果你和我一樣是投資人,還是建議採取上述比較嚴謹的隨機積分數學模型,以利後續修正和計算。
不過如果妳是路人,可以採用這個簡易版本。
事實上,我推薦過的"The Long Term Behaviour of Leveraged ETFs",以及文獻版本"Alpha Generation and Risk Smoothing using Managed Volatility",文中也這樣寫。
作者沒寫推導,我在這邊親自寫一次。
過程可能會有出入,妳如果不滿意也可以採用自己的方法。
我們先來看幾何平均和算術平均的關係。
如果一個資產經過兩期就變成四倍,那麼算術平均報酬是150%,幾何平均報酬是100%
在比較短的觀測期內,我們會假設股票線性上漲,可是時間拉長,我們會使用冪成長模型。
所以短期用哪一種平均算法都可以,但長期而言兩者會有差異。
現在我來找幾何平均報酬的近似值。
用Taylor series逼近前兩項
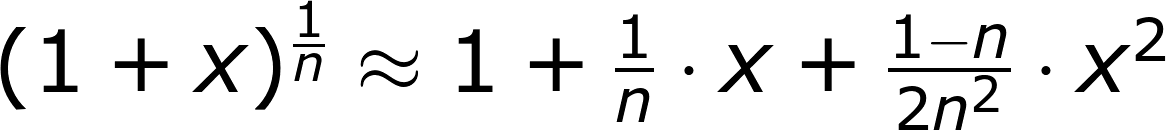
我們可以用連續相乘表示長期報酬。
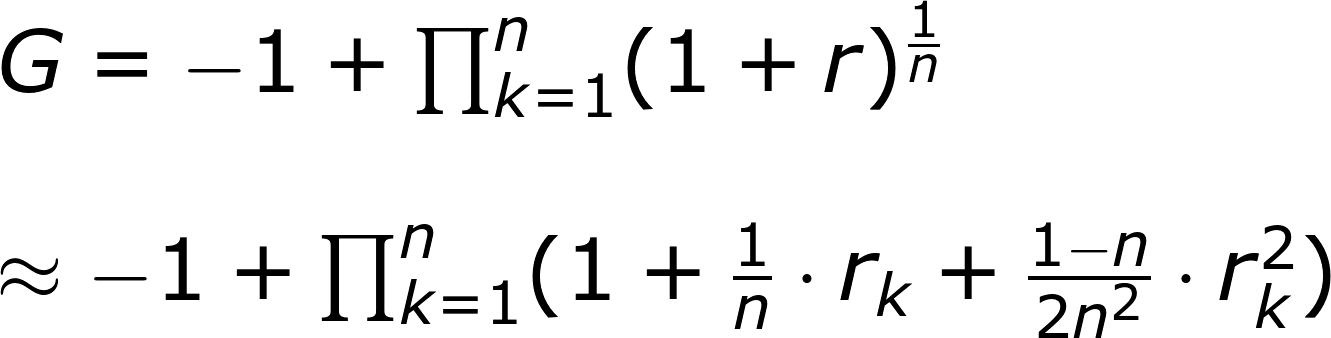
G: 幾何報酬的成長
Π: 連續乘法符號
我們可以忽略掉n³和更高次,所以只需考慮各項和1的相乘,以及1/n和自己相乘。
不過實際上不會真的乘到自己,所以符號需要微調。
原式變成
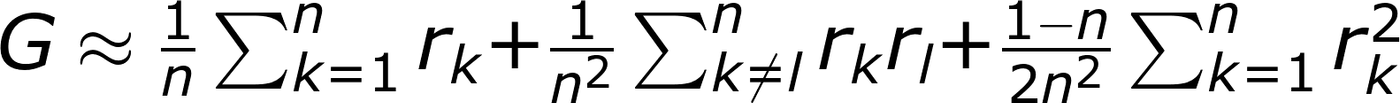
Σ: 連續加法符號
接下來,我們考量算術平均和變異數。
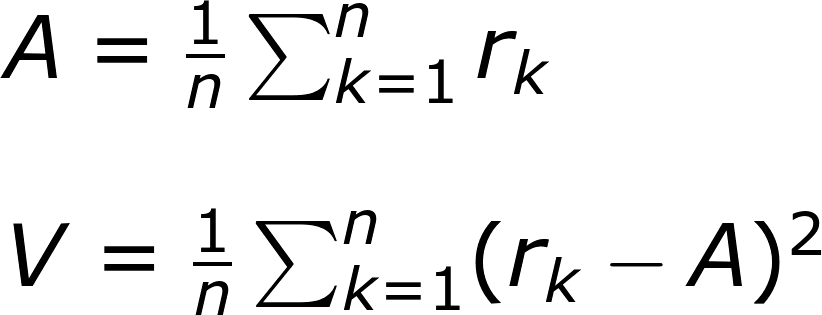
A: 算術平均
V: 變異數
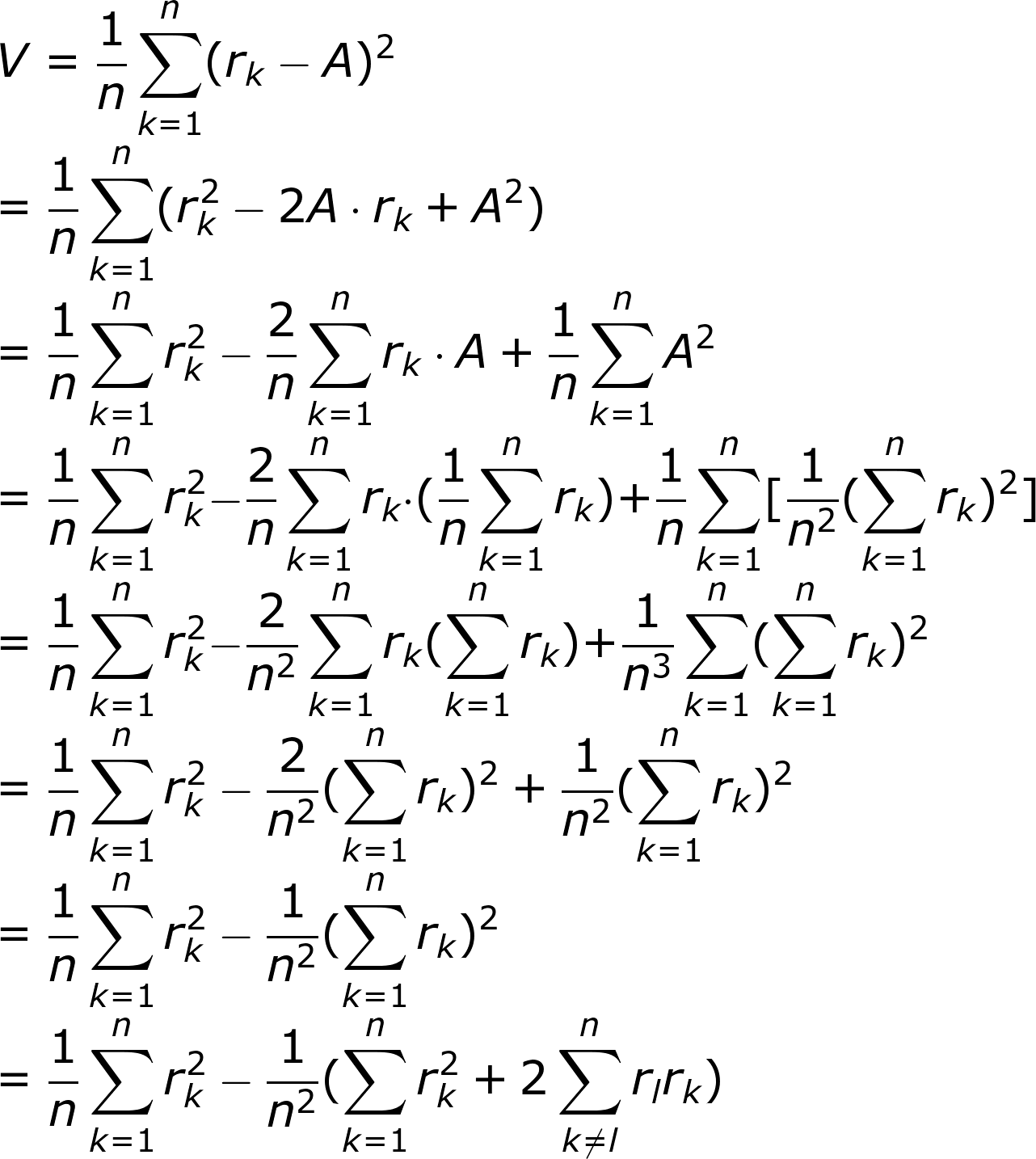
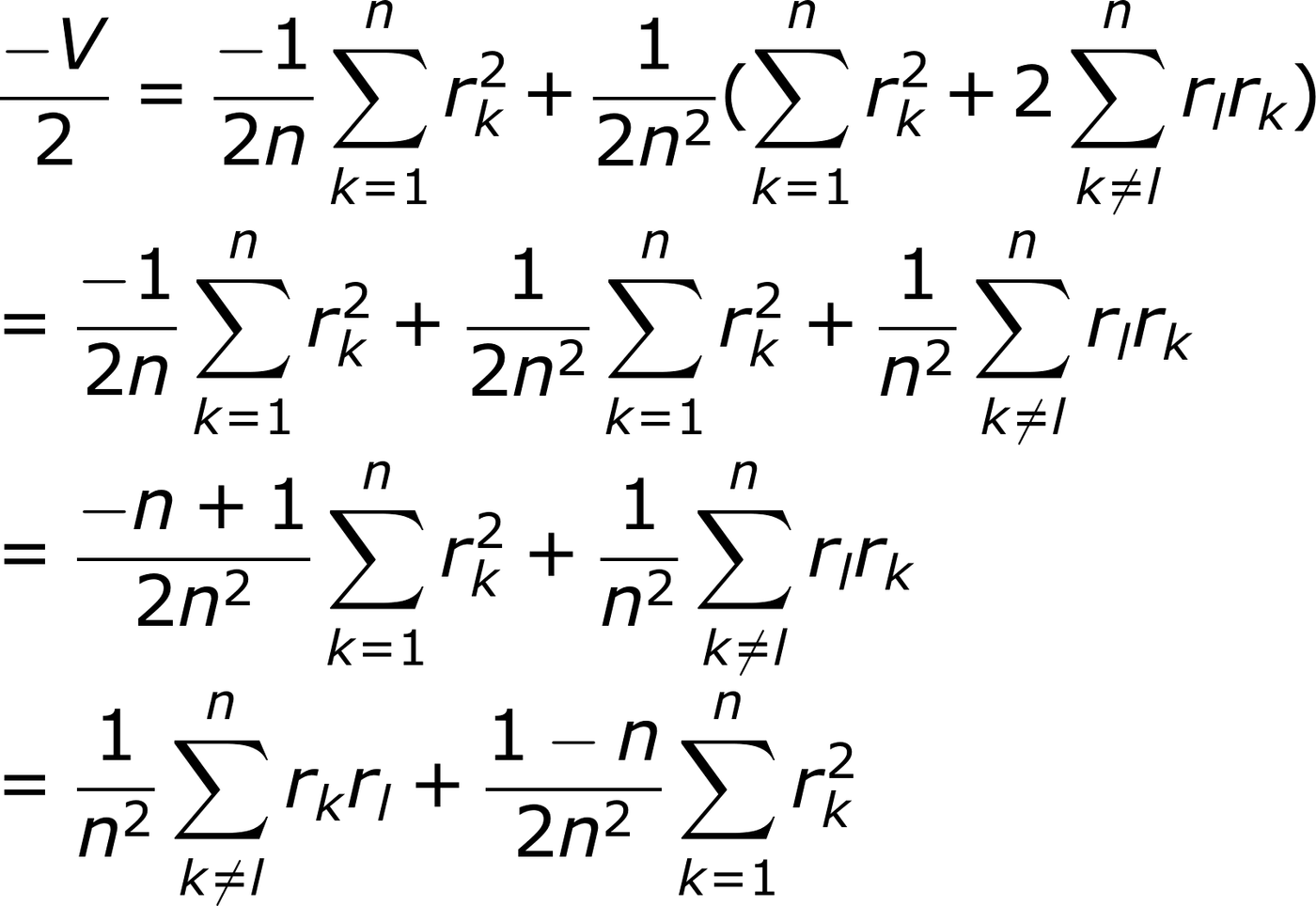
我們發現
G=A-V/2
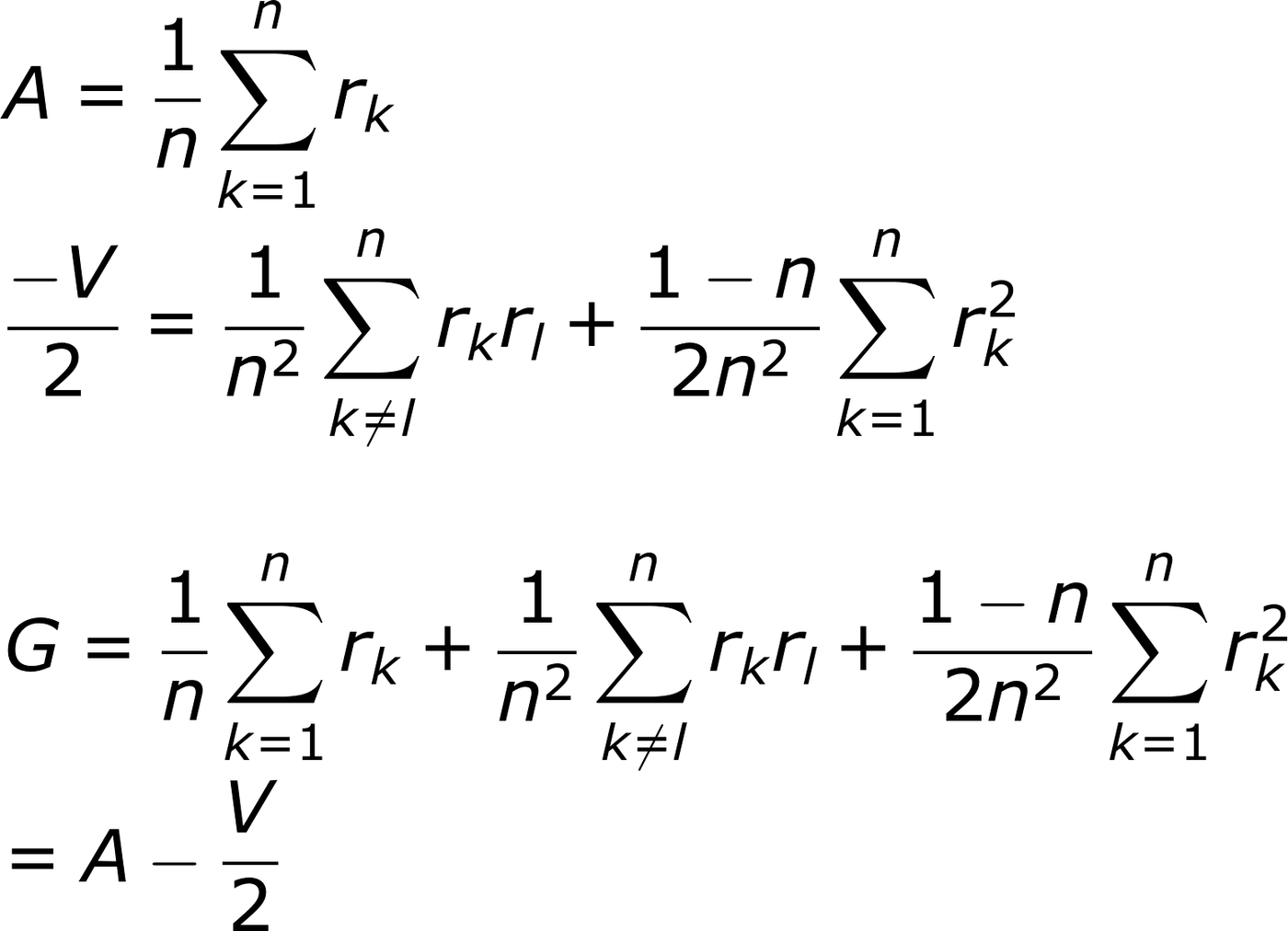
順帶一提,聽說金融相關科系的朋友會知道這個近似公式。
現在

注意,k倍數值,造成k²倍的變異數。
R: 幾何報酬
A=kμ
V=k²σ²
接著就是老把戲,將原式對k偏微分求極值,極值所在就是最佳槓桿倍率。
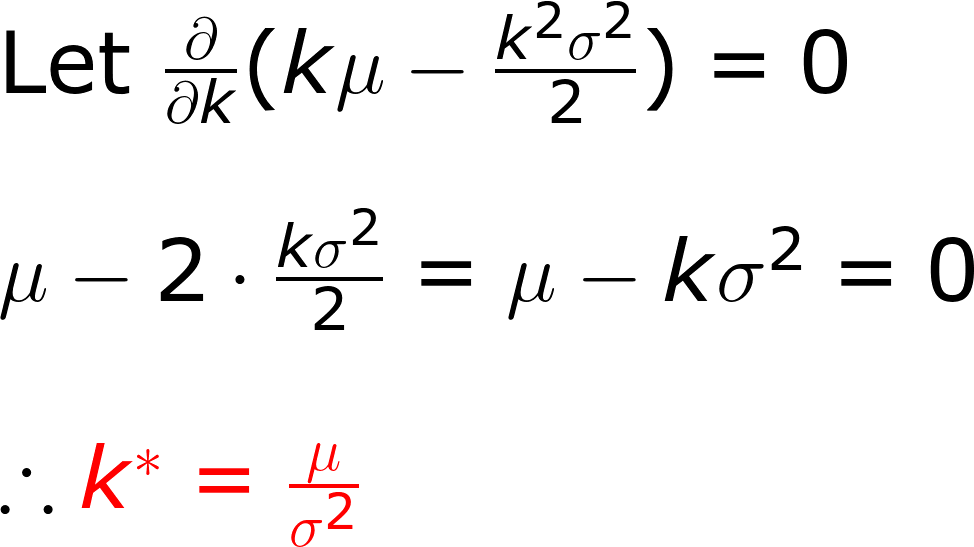
我們得到最佳槓桿倍率。
8. 基本教義的文化陷阱
如果妳每天半夜嘴饞叫外賣,結果體重迅速增加,妳會去怪外送員或食物嗎?
或是你晚上不睡覺,隔天覺得精神差,你會很意外嗎?
我自認是新手,也一向尊重讀者的自由意志,所以我不會混合討論工具和「心態」或「自制力」。
投資人如果有可行的策略,卻因為人性而虧損,完全是自己的問題。
我講求科學證據和推論,不常談論人性缺陷造成的失敗。
如果你習慣把一個長期計畫中斷,我建議你根本不要進入風險市場。
另一方面,有些作者會提醒讀者小心使用槓桿,也有人知道自己不了解槓桿機制而主動遠離,這些都是「正確且負責」的做法。
有人因為主觀原因而對槓桿批評或推崇,也屬於中性行為。
但還有一批基本教義教徒練功走火入魔,一定要別人照著他們的意思做。
你想要買高級刀具,所以走進廚具專賣店,結果一群人擋在門口,告訴你刀子很鋒利、很危險、很多法外狂徒都拿刀......
妳想要買跑車,走進汽車專賣店,結果一群人把妳拖出展廳,告訴妳開車很危險、很容易出車禍、很多法外狂徒都飆車......
這不是關心,這是找藉口阻止妳,表演給信徒看,用「正確的廢話」掩飾自己的無知。
很多提過ETF的業餘投資作者都在開會員、賣課程、收學生,但不是每一個人都有辦法承認錯誤,妳聰明就顯得它愚蠢。
他們不喜歡信仰被打破的感覺,又不知道槓桿背後的原理,無法理性反駁,所以找一堆理由濫竽充數,於是討論最終缺乏實質意義。
我尊重知道自身狀況而長期堅持的投資人,我反對道聽塗說、聽風是雨還拒絕成長的信徒。
有一群人在討論中求知,雖然意見通常不同,但是能得出嚴謹的結論,進而傳播知識。
另一群人,自己尚未了解,或是沒有能力了解,也不想讓後進者獲取知識,所以蒙蔽其它人的眼睛。
我從頭到尾沒說自己支持或反對槓桿和相關工具,我批評的是反方垃圾理由。
你可以說內扣太高、轉倉太麻煩、槓桿率不便固定......結果一群人拿「耗損」出來當擋箭牌。
如果有人說波動太大會讓人難以堅持投資計畫,那就罷了。
一定要把內扣和槓桿波動的特性混在一起,把一個產品說成天生吸血的生物,還裝模作樣用表格來證明,有意義嗎?
就憑這種伎倆,妳也只能欺負那些不懂做實驗的信徒而已。
我對半桶水沒有什麼耐心,一句話幹死。
「0.5倍槓桿的耗損在哪裡?」
大家喜歡的話也可以自己玩看看。
再說另一個分支,有人堅持投資不能接觸槓桿。
我懷疑它們來自月球,剛下飛船。
金融,就是資金的「融通」,什麼意思?
槓桿啊, baby.
借貸利率、外匯存底、國家債券、公司股票......哪個沒有槓桿?
這裡是地球,人類社會就是由不同倍率的槓桿組成。
重點從來不是有沒有槓桿,而是倍率本身。
我說過,槓桿是指數投資內戰的熱門題材,很多衝突源自基本教義派的狂妄。
狂妄本身很好,看看老子姓什麼,確實應該自豪。
但是沒本事還學人家狂,到處攻擊其它流派(包括指數投資中立派也中槍),那這些人就是欠教育。
我曾請教台灣某指數作者,他用期貨來控制自己的倉位,槓桿倍率略大於一。
妳隨便問一圈就會知道他算是圈內元老,但這種作法還會遭到非議,因為教義上寫,接觸槓桿就是大逆不道。
不論是期貨、槓桿ETF或貸款,只要槓桿就不行,只要非本教義派就都是外道。
我心臟比較小,手中留有現金? 不行。
Cash drag.
我心臟比較大,使用槓桿ETF? 不行。
Volatility drag.
在基本教義信徒眼中,槓桿倍率只能「剛好」是1.00000000000000000
有不少人就是企圖告訴大家,世界上算他最聰明,其它人都不會思考。
所以我之前就用同樣的話,拉同樣的表格,宣布who's your daddy.

話說到這裡,讀者朋友可以自己決定。
你相信正統教廷的權威和千百年來的普世信仰,還是那些堅持「地球依然在轉動」的邪教異端?
我無法阻止其它人寫出錯誤的觀點,但我可以在實證和理論層面傳達正確的知識。
我覺得自己的這種嗜好,有點像海中的鯊魚,不停游動前進,而且在知識層面嗜血。
有人想加入鯊魚教嗎?
Daddy shark doodoodoo :)
9. 波動率聖杯
有些教主喜歡說槓桿ETF一定會造成耗損,長期下來會歸零。
那恭喜了,他找到聖杯。
稍微動點腦子,就會知道市場上沒有什麼「一定」。
持有正向槓桿ETF,就是在做多長期走勢,同時做空波動率。
所以如果長期走勢不明顯、波動率又大,那投資人就會承擔虧損。
你都確定市場會這樣走,為什麼不倒過來做?
我曾提過自己同時「賣空正反向槓桿ETF」的作法,例如SQQQ/TQQQ,在貿易戰剛開打的時候遇到很多同好,還有人跟單。
好像又是一個邪教歷史了,不過我可以和各位分享其中的原理。
我們做空部位相反的兩個ETF,例如正一/反一、正二/反二、兩份正三/三份反二,並隨變動調倉。
如此一來,投資組合就是Delta中性,因此資產本身的價格走勢不會直接影響獲利。
相對的,由於持有槓桿ETF是做空波動率,所以做空這些ETF相當於做多波動率。
也就是說,如果你押注波動率上升,就可以賣空一組槓桿ETF,而且槓桿倍率越大,效果越明顯。
順帶一提,投資人不希望遇到上漲或下跌的單邊走勢,原地震盪盤最能獲利,因此這個策略也算是short Gamma.
除了股票市場,原物料或匯率市場也有許多交易波動率的工具,我猜那些領域的槓桿ETF因此有了生存空間。
不過工具是中性的,你從這個角度也可以看出,根本沒有所謂的「一定」耗損,因為沒人知道之後的波動率會上升或下降,我也不特別鼓勵賭波動率。
10. 槓桿再平衡頻率
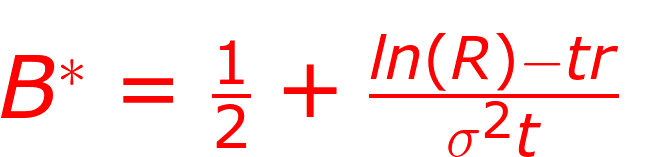
我們先看投資人版本的最佳槓桿率,忽略掉借貸利率(槓桿ETF內扣已包含),如果指數長期原地震盪,那0.5倍槓桿最合適。
因為波動率曝露比較少,所以反而會贏過指數表現。
那如果指數會上漲呢?
事情就變得有趣了。
我說t是時間,真正的意思是總期數。
如果一期是一天,那一年就有約252期;一期是一個月,一年就有12期。
假設股價波動是Gaussian(常態)分布,那麼變異數(σ²)會和時間成正比,如此一來無論t取多長,σ²t不變。
可是如果每一期拉長了,那麼R會變大,ln(R)稍微變大,因此會讓最佳槓桿率提升。
所以我們知道,把單期拉長可以提高最佳槓桿率。
另一方面,如果固定槓桿率,特定的槓桿平衡周期會提高整體報酬。
以2010年初到2020年末的NASDAQ超強走勢為例,指數變成5.58倍,指數單日三倍槓桿是47.9倍,而指數單月三倍槓桿是88.5倍。
看起來似乎時間拉越長,報酬會越多,可惜事情沒有這麼簡單。
如果妳用一年當單位,那麼總倍數是85;如果用十年當單位,總倍數是16.7倍。
換句話說,在固定槓桿率之下,我們可以找出一個最佳平衡周期。
那為什麼會這樣呢?
想像一下資產的波動特性,通常短期的標準差很大,但時間拉長之後會逐漸收斂。
因此時間越長,資產走勢會越貼近冪成長。
如果周期太短,指數型成長還未成形,單期波動是主角,所以持有正向槓桿ETF相當於單純做空波動率而已,漲幅不明顯。
如果周期太長,冪成長已經非常明顯,我們卻用原指數的緩慢成長來當基準,漲幅也會被限制。
所以最佳區間就是資產有一點上彎的造型,但又還看得出一些波動的周期。
以全世界的股票大盤來說,三倍槓桿的最佳平衡周期在兩到三年,而不是二十年或單日。
11. CVaR和VaR
定槓桿投資也太簡單了,找出最佳槓桿率和最佳平衡周期,就可以耐心等資產暴漲......
如果是這樣,我會寫出來嗎?
有許多讀者問我期貨和槓桿ETF的優劣,嚴格來說兩者有同樣的底層概念,只是交易人不同,我猜大家更關心的是槓桿頻率對應的風險和報酬。
再次召喚指數投資的朋友,各位可能都聽過「不用停損」這種說法。
由於資產指數長期上漲,所以停損也沒特殊意義。
換句話說,最慘的狀況下,我們大不了被套牢久一點,只要資金還在市場上,就有恢復的一天。
現在,當槓桿倍率比一還大的時候,有可能發生市場下跌、部位中途爆倉的狀況。
就算大盤恢復了,投資人手中的部位還是0
因此通常我們在考慮極端風險的時候,會比較愛用VaR/CVaR(風險價值),用置信區間來估算損失超過特定「門檻」的風險,其中的應用包括心理防線和margin call.
從這個角度,妳也知道為什麼有人說槓桿ETF比期貨還安全。
以各種指數為例,一個月下跌超過三分之一很容易,例如2020年3月。
相對的,一天之內下跌同樣幅度,幾乎不可能,目前紀錄是1987年黑色星期一的一日22%
所以三倍槓桿ETF能持續存活,但是三倍槓桿期貨會歸零。
如果我們從波動風險考量,會發現長槓桿平衡周期比較有利,但從風險價值的角度考慮,會得出更保守的答案。
妳可能會覺得我常常提Sharpe/Sortino,凡事以此風險指標為準。
但事實上,我要求Sharpe的前提是策略要能搭配槓桿,同時把二階矩(標準差)這個限制拿掉,全心考慮獲利。
如果不調整槓桿,那高波動報酬比只不過是讓曲線好看,對我的資產累積並沒有幫助。
實務上由於槓桿投資人很常放大波動率,因此開始需要考量小機率的狀況,其中的指標就包括CVaR,而相關的投資組合優化就會用到mean-CVaR.
加入這種約束條件後,我們知道就算以期貨長期定槓桿投資,最佳槓桿區間也不過在二左右,三倍已經算危險了。
因此,我認為兩種工具都很好用,但期貨族如果調整出較為有利的定槓桿,多半是因為承受更高的尾部風險,而不是憑空額外獲利。
12. 尾部風險和邪教
寫了六千字,如果我說「我才剛要切入正題」會不會很好玩?
開玩笑的,再寫下去可能突破一萬字。
我先介紹兩位「邪教狂徒」,各位應該聽過我持續的推薦。
第一位是Mandelbrot,碎形幾何之父,寫過《股價、棉花與尼羅河密碼》(The Misbehavior of Markets)
妳可以Google doodle

想知道碎形和金融市場的關聯,讀者也可以參考「遠得要命的數學王國」寫的文章。
當時Mandelbrot提出很多看似標新立異的理論,嚴重挑戰現代金融學的根基,不過直到後來世人才逐漸了解他的前瞻性。
不論碎形是否能解釋價格變動,我們都知道波動分布並不是Gaussian.
這下子事情非常嚴重,金融的理論大廈可能會被摧毀,因為人們總喜歡「假設波動服從常態分布」。
如果這個假設出錯,我上面寫的VaR/CVaR、最佳槓桿倍率、Delta/Gamma、布朗運動......全部都會被掀翻。
各位請別小看常態分布的特殊性,它的偏度和(超額)峰度是0,而且擁有二階矩(方差)和有意義的「平均」。
因此金融界大量用到常態分布的對稱性,而且以平均定義報酬,以變異數定義波動風險。
就算價格不是常態分布本身,lognormal(例如GBM)的矩生成函數也相對單純。
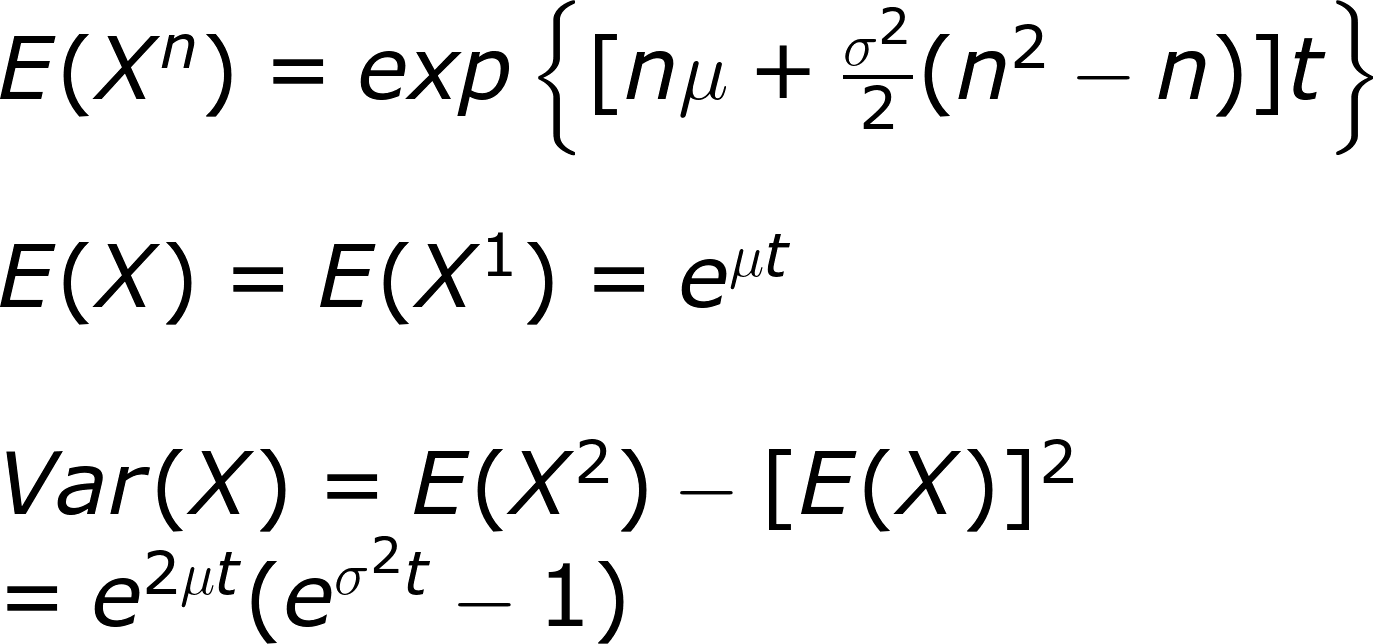
很多人習慣套用常態分布在任何和股市有關的波動,而這就包含現代金融用戶和信徒。
然而仔細思考,就會發現很多理論的假設過於簡單,甚至自我矛盾。
「狂徒,怎麼又有信徒出現了?」
我舉個鐵鎚教徒的案例。
如果布林通道那派雙標準差的上下軌對股價合理,那它對槓桿產品就會失效。
這是很純粹的矛盾,因為價格呈現常態分布,連續定槓桿的價格就不會是常態分布。
我還真的看過一些人把布林硬套到槓桿ETF上,就像手中拿鐵鎚,看到每個物品都覺得是釘子。
我再往上推一階,也就是lognormal的偏度。
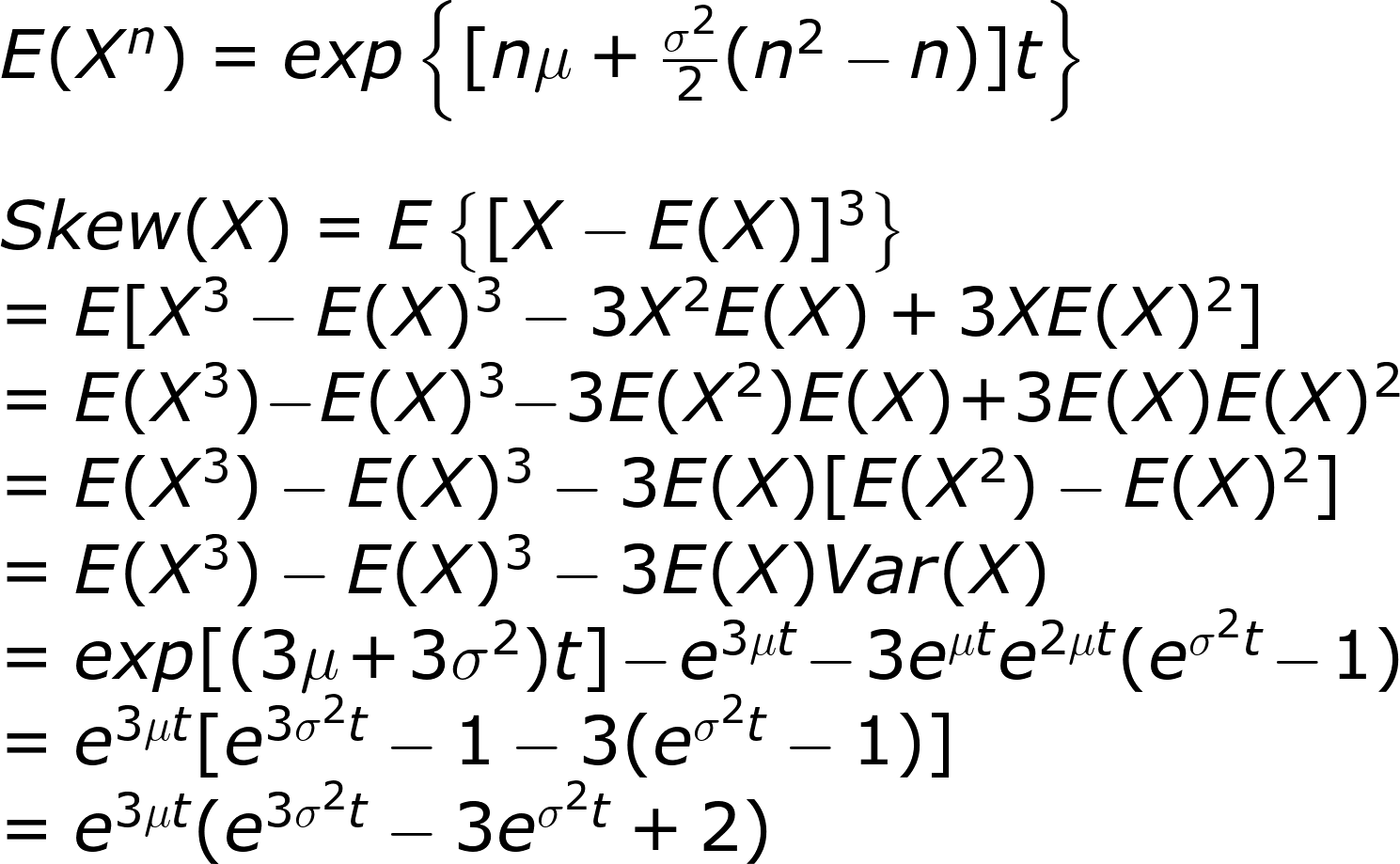
你覺得,這串偏度算式長得很像0嗎?
偏度、變異數、均值都和常態分布不一樣,布林怎麼用?
對於現代金融理論的大多用戶而言,不會犯上述低級錯誤,但本質上還是都從常態分布出發。
事實上,如果基本假設不成立,我可能連算都不用算。
人們當然會思考真實和理論的差異,但許多人在遇到困難後也只能妥協,以有瑕疵的作法繼續完善人類的知識框架。
現在我要介紹第二位狂徒,Taleb.
他很可能是我提過最多次的傢伙,目前還很活躍。
Taleb的研究橫跨多領域,同時是期權交易員和風險工程教授,寫過《黑天鵝》和《反脆弱》,我推薦過他的《動態對沖》和《肥尾效應》。
他是很標準的投資無神論,而且有業界、學界和寫作圈的經驗,非常喜歡依靠自身強大的知識,推翻金融世界的既有規則。
重點是,他在diss人也毫不畏懼,我提過前幾年的Taleb大戰Asness(AQR老大)就是一個最佳證據。
簡單來說,他很狂、很嗆,常常講出讓普通人覺得莫名其妙的話,而且四處征戰,例如公開點名Fama/Merton/Markowitz等泰斗。
他除了在網路上混,也身處市場第一線,而且還在學校教書,偶而又會出書。
一般人不管從什麼角度想攻擊都沒有勝算,所以通常選擇安靜或直接忽略。
最邪門的地方來了。
你剛接觸金融的時候,可能會接受他的觀點;你以為自己有點知識的時候,會覺得他講外星語言;可是當你再進階的時候,會發現他有正確的切入點和證據。
就如同他推崇Mandelbrot一樣,基於研究、實證、質疑、掀翻權威、走出象牙塔的角度,我也推崇Taleb.
無它,我太懂這種感受。
小學中年級,有個數學老師知道我很叛逆,不喜歡背課本上的條文,例如「三角形內角和等於180°」。
結果他送我歐基理德的《幾何原本》,同時告訴我,在球形和鞍形空間內第五公理失效。
升上高年級,我就到處拿黎曼幾何和羅氏幾何,去和歐氏幾何的同學吵架。
我用粉筆對抗一堆人的數學習作和量角器,直到自然和社會教到地球經緯度,幾個比較聰明的同學安靜了......
知識的突破,哪一次是標準答案?
回到槓桿和槓桿ETF,如果股價波動並非常態分布,怎麼辦?
萬一真實世界的報酬分布是「狂野Cauchy」,我根本不知道平均是什麼,其它二三四階矩也都沒定義,還要怎麼玩?
有幾個可行的方法,包括長期持有和資產配置。
長期持有會讓均值逐漸收斂,資產配置表面上也會讓波動快速減少。
股市雖然不是Gaussian,也沒有Cauchy這麼狂,所以人們喜歡用GED/Student/Beta/穩態分布......
如果從純數學的角度來看,大數定律存在,但收斂速度很慢。
而對於多類資產配置而言,也容易呈現因為觀測頻率而造成的安全假象。
不過實際上,投資人基於穩健性(Robust)優化,本來就不應該過於將波動往尾部推進。
Max Sharpe的Markowitz均值方差法和效率前緣,就容易因為均值估計不易而讓投資組合比例大幅變動,也因此後續才有Black Litterman和Risk Parity等寬鬆方法。
白話文,不要把投資槓桿率壓在最佳區間,應該要降低一些,而且搭配不同資產,並長期持有。
從尾部風險考量,非常態分布的世界很有趣。
PCA和因子分析,因子投資的OLS,資產組合的共變異數矩陣/二階矩最優化,Beta/Sharpe/Sortino,資產的風險對沖,全部都會受影響。
因此,讀者朋友最好預先設定最差狀況,而期待有更差狀況出現,這才符合肥尾精神。
我基於常見的基礎模型推導最佳槓桿率,是提供入門後修正的橋樑,不是傳播「標準答案」。
我反對Taleb對槓桿和資產配置的反對,但我也不認為市場「安全」,因為我能掌控的風險都不叫真正的風險。
長期固定130%到150%槓桿,安全。
長期持有200%倍率的多資產大盤槓桿ETF,還算安全。
至於4/5倍的槓桿ETF,我看不出長期持有的理由,你需要準確的擇時才能應對,知易行難。
13. 因子、槓桿、尾部
有讀者問過我,(風格)因子投資是否能結合槓桿,例如SAA(小市值因子雙倍槓桿ETF)。
我認為廣義而言,因子投資和對尾部風險的考量能夠增加投資人的優勢。
因為在這個層面,我們把因子/槓桿資產/資產/組合全部視為報酬和不同風險的呈現,所以投資人才能無障礙的融合。
換句話說,有人借貸買因子ETF,有人買槓桿因子ETF,有人期貨槓桿買股票、額外又做多因子......這些行為不應該是抉擇,而是透過優化框架合理併行。
不論是資產本身或因子,報酬分布都有肥尾現象,不適合用常態分布來應付,因此以Lagrange算子和反矩陣的那招MVO非常需要修正。
另外關於協方差,因子之間的相關性並非一成不變,有可能在劇烈波動的時候趨同,導致因子配置的分散優勢降低。
有沒有改革方法?
資產配置有前三階/四階的優化方式,也有放棄預測收益的風險預算方式,還有融合因子和熵的組合方式。
如果把動量、價值、品質、成長、波動、槓桿、偏度等廣義因子的三四階矩都估算出來,就可以沿用傳統處理資產的方式。
以Risk Parity為例,JPM上就有"Extending the Risk Parity Approach to Higher Moments: Is There Any Value Added?",透過Tensor/ 4D Tensor來優化配置。
而因為跳脫常態分布的限制,因此整體穩健性和風險報酬比都能增加。
這時,槓桿因子、因子的槓桿和融合因子優化的組合槓桿,不再是雜訊,而是武器。
14. 「狂徒,你整篇都寫錯了,回去重練。」
接下來我列出反面意見,供讀者繼續思考。
首先,既然槓桿機制不是只有我知道,它就有可能早已被price in.
例如我買槓桿ETF就會牽動到期貨,期貨又會影響指數本身。
不論我用什麼方式調整,市場上一定會有相反操作,那我要如何確定這麼做勝算較高?
其次,所謂最佳槓桿率,是建立在波動率和預期報酬上,但是市場波動本身還會有偏度/峰度和更高階矩,所以模型不精確,尤其在於尾部風險,例如黑色星期一。
既然肥尾分布象徵災難可能比想像中的最差狀況還糟,而且不是每個分布都有高階矩,那麼我這種往高階貼近的作法適合嗎?
第三,前面槓桿產品報酬的公式,都建立在幾何布朗運動上,但萬一股價不是二階的變分有界,整串公式需要改寫。
第四,我完全不考慮時序相關,直接帶入隨機微積分。然而時間序列會有些微相關,例如市場情緒/總經,所以我們會知道波動率呈現均值回歸/clustering/槓桿效應,那我要怎麼修正?
繼續用同方向的Heston隨機波動率,或是Merton跳躍擴散但依然用IID? 還是加入GARCH,持續用二階的heteroskedasticity?
最後,市場和任何模型都不完美,在近似的路上走下去,非常有可能因為沒考慮到某項因素而造成災難性的結果。
例如用電腦模擬半天,結果基金公司突然宣布倒閉,就有可能讓投資人措手不及。
現在妳知道怎麼用槓桿ETF的原理和反方吵架了,但下次遇到支持方,不妨參考以上的論點。
15. 結論
證交所、各國基金公司和很多老師都宣稱槓桿ETF不能長期持有,實際上就是這種思想讓它變成投機工具。
槓桿ETF和期貨屬於中性工具,我建議多元分散、長期持有和控制成本(指數投資教義),不過你要短線持有也是自己的事情。
對於有上漲特性的資產,例如股票,可以單獨持有槓桿ETF,但最好搭配其它資產類別。
對於無內部價值的石油、匯率、原物料、貴金屬等,槓桿ETF只是在曝露波動率,長期持有也不會有意義。
最佳槓桿率會變,長期而言股市大盤倍率略等於二,短期有可能掉到一以下或變成負值,幾乎不會剛好是一。
所以長期持有正向槓桿ETF或期貨,會因為多承擔風險而換取更高報酬。
這不是真正的打敗大盤,只能算公平交換。
不論是路人還是投資人版本,都有一定誤差和失效風險,所以投資人採用倍率應該比最佳區間更保守幾分。
市場要是這麼好掌握,基金公司還丟出來賣?。
隨波逐流的是信徒,興風作浪的是狂徒。
遠離基本教義,保持獨立思考的能力和批判的習慣,自然會對投資更有信心。
或許理解槓桿ETF不是簡單的過程,不過當妳都能吸收、實踐之後,可以回過頭看看各路高手的文章,就會發現「坊間專家」和「槓你老師」為什麼總比不上「投資人」了。
後記:
槓桿因子是風格因子,描述公司資產負債比。
槓桿/反槓桿效應是波動率的時間序列特性,描述漲跌和波動率的關聯。
因子槓桿ETF是因子單日倍率曝露ETF,商品機制和大盤槓桿ETF相似。
非一倍槓桿ETF和原型ETF都是投資大盤,而且注重長期持有和多元分散,難度會突然往上跳是因為它涉及波動率,而且通常會讓尾部風險增加。
平時指數投資人和ETF最接近,但看不懂槓桿ETF,而且既然投資策略不包含尾部風險,也不理會波動率,所以作者不需要自找麻煩。有趣的是,真正需要交易波動率的人,會傾向使用期權和期貨,也不太用到槓桿ETF. 這造成兩批人馬沒有交集,常碰的人看不懂、看懂的人不常碰,所以槓桿ETF就被放在真空地帶,被自以為聰明的大師當投機工具。
久而久之,槓桿ETF就變成邪教名詞。
逆風好玩嗎?
當然。
2000多年前,畢達哥拉斯就是數學之神,他說的話就是教義。老畢錯誤的認為所有數字都是有理數,而信眾也非常虔誠。據說,那位發現「根號二」的學生希帕索斯,喜歡講真話又不肯妥協,引發第一次數學危機,所以被丟入海裡淹死。
在這個民智漸開的社會,各路作者不用擔心違反圈內基本教義的意志而被處決,因為知識就是最強的武器,能夠拿下一座接一座的城池。
雖然我不喜歡牆頭草/假中立,不過我也知道這是普通人的特性。
作者大仁提到:「在今年以前你提到槓桿 ETF,可是會被當成笨蛋才會投資的東西。在台灣是完全的逆風,而且是颱風級的大逆風。」
我也說過:「我就是喜歡狩獵,我享受把逆風轉成順風的過程。」

同樣都是寫文章的作者,為什麼風格差這麼多呢? 因為需求層級不同。
有人想開課賺錢,屬於求溫飽的生理需求。
有些人想要交換意見、尋找同溫層,滿足社交需求。
有作者想要累積信徒、獲得成就感,這是更高層級的尊重需求。
還有一種作者,寫爽的,這叫自我實現需求。
我要的是挑戰潛能和超越自我,我也成功的讓一段時間前的自己看起來很菜。
有些作者朋友不懂,為什麼我會寫出只有1%讀者看懂的文章,既沒有流量又沒有收入,寫完還會失去追蹤者。
倒是教育界的朋友懂我,處理大量資訊和高強度思考是我的紓壓方式,追求「高峰經驗」和靠真理打下來的江山,比空虛的信徒和基本教條有實際意義。
我打的每一個字、每一行公式,都是串接知識的橋樑。
我盡量確保內容正確,所以我也常常為了解釋一個冪次或正負號思考一整天。
自我正反論證,不但是能增加資產的思考習慣,也是帶有藝術性的遊戲。
狂歸狂,浪歸浪。
如果我有寫錯的地方,歡迎公開或私下踢館。
Thanks in advance :)
參考:
Stochastic Differential Equations
Extending the Risk Parity Approach to Higher Moments: Is There Any Value Added?
Path Dependence of Leveraged ETF Returns
