「谷歌」64 ~ 最小的路径和
基本信息
题号:64
题厂:谷歌
难度系数:中
已知一个 m * n 的矩阵,矩阵格子里有一些数字。问从左上角走到有下角,最小的路径和是多少?
(只能往右走,或者往下走)
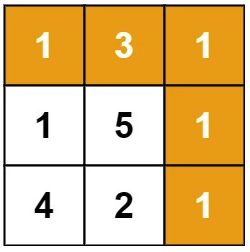
如上图所示,从左上角到右下角的最小路径和为 1 → 3 → 1 → 1 → 1,加起来就是 7……解题思路
欲解此题,需要具备一些 recursive (递归)和 「动态规划」(dynamic programming)的基础……
默认具备「递归」思想和「动态规划」思想后,再来进行化繁为简初步分析。
1 * 1 的格子

显而易见,只有一种走法,或者根本就不用走,直接返回格子数本身——1.
1 * n 格子

当矩阵只有一行时,还是只有一种走法,4 - 2 - 1,走法。这里运用递归思路,我从 4 走到 2,没走完,接着走直到走到 1 可以结束程序,路径和为 4 + 2 + 1 = 7.
n * 1 格子

此案例和一行矩阵思路类似,只有一种走法。1 + 1 + 1 = 3
多重走法
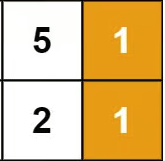
只有行和列同时大于 1 时,才可能出现多种走法。例如 5 - 1 - 1, 5 + 1 + 1 = 7 和 5 - 2 - 1, 5 + 2 + 1 = 8. 择优后选择 5 - 1 - 1 走法,最小路径和为 7.
经过以上分析,我们可以从基本款(1 * 1 矩阵)入手,不断计算所有走法,然后再择优返回所有走法的最小值,即可完成任务。
以上思路可以通过「递归」来实现代码
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
ROW, COL = len(grid), len(grid[0])
# 创建递归方法
def recursion(i, j):
# 当行列为 1 时,返回格子本身(只有一种走法)
if i == j == 0:
return grid[i][j]
# 当只有 1 行时,只有一种走法,返回所有格子和
if i == 0:
return grid[i][j] + recursion(i, j - 1)
# 当只有 1 列时,只有一种走法,返回所有格子和
if j == 0:
return grid[i][j] + recursion(i - 1, j)
# 当有 1+ 行 和 1+ 列时,我们选取较小的那一款走法,递归计算
return grid[i][j] + min(recursion(i - 1, j), recursion(i, j - 1))
return recursion(ROW - 1, COL - 1)以上思路无逻辑错误,但复杂度太高,无法满足题目需求。所以需要优化……
根据默认解题经验,递归的最优解一般就是动态规划。动态规划的原理和递归有类似之处:都是化繁为简,从最基础模式开始思考,逐步发展找出规律(后面的计算可以从基本模式发展演算),类似于高中数学等差数列找规律再总结公式的套路……
那么本题的规律也很容易发现:格子只能从上边或者左边发展过来。如果从上走过来小,就择优选择从上走;如果从左走过来小,那就择优从左走。而上一步又可以不断往前知道 1 * 1 只有一个格子时。而在这个过程中,我们可以记录走到下一步需要的路径和,当有多种走法的时候就择优累加即可,达到简化代码和复杂度的作用。
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
ROW, COL = len(grid), len(grid[0])
# 创建一个和题目已知矩阵相同的矩阵,用于记录走到该格子的路径值
path_grid = [[0] * COL for _ in range(ROW)]
# 初始化第一个格子
path_grid[0][0] = grid[0][0]
# 初始第一行
for c in range(1, COL):
path_grid[0][c] = path_grid[0][c - 1] + grid[0][c]
# 初始第一列
for r in range(1, ROW):
path_grid[r][0] = path_grid[r - 1][0] + grid[r][0]
# 根据初始值,计算后续发展
for r in range(1, ROW):
for c in range(1, COL):
path_grid[r][c] = grid[r][c] + min(path_grid[r - 1][c], path_grid[r][c -1])
return path_grid[ROW - 1][COL - 1]达成以上动态规划后,我们可以在此基础上做进一步空间复杂度优化:
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
ROW, COL = len(grid), len(grid[0])
base = [0] * COL
for i in range(len(base)):
if i == 0:
base[i] = grid[0][i]
else:
base[i] = base[i - 1] + grid[0][i]
for r in range(1, ROW):
for c in range(COL):
if c == 0:
base[c] += grid[r][c]
else:
base[c] = grid[r][c] + min(base[c - 1], base[c])
return base[COL - 1]Constraints
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
测试
m = n = 1 时
当只有 1 列时
当只有 1 行时
当有多行多列时
当 m = n = 200 时,测试代码有效度
……
Big O
时间复杂度:O(m * n)
空间复杂度: O(n)
总结
这类题可以划归为「矩阵 + 动态规划」递归题型,它们拥有相似的模板和相同的套路
通过比较「递归」模板和「动态规划」模板的异同,理解如何通过「动态规划」达到最优解
相似题型:62, 63, 174
