SNN初探(3)──監督式學習SpikeProp
(由於我不是原作者,只是一個傳播內容的媒介,因此接下來我會以解釋該論文的思維為主,不帶有任何性能與效能上的評論)
已經以大眾能理解的角度去講解數學的推導,本文之後,算是一個我認為可以到此為止的段落。因為已耗費大量精力,往後我不會再提到關於SNN的其他議題。
在撰寫SNN的演算法時,我遇到非常大的困難點。關鍵在於實行演算法之前,SNN網路的參數定義是非常重要的。如果沒有辦法用程式碼定義neuron、定義PSP的形狀、定義時間軸,談算法都是枉然。因此撰寫這篇主要是幫助我釐清一些沒被定義到的參數、還有介紹SNN最早的監督式學習方法SpikeProp。
前面提到SNN大多用於分類問題、而少用於解決擬合問題。因此,非監督式的方法在SNN上應用較為普遍,其中最著名的,就是STDP(spike-timing-dependent plasticity、依賴脈衝時間之可塑性)。STDP的概念簡單來說,就是越靠近spike觸發時間點 之前 的PSP、可被認為是跟該spike最有關係的輸入訊號。反之,越靠近spike觸發時間點、卻出現在觸發時間點的PSP、則是最無關係的輸入訊號。可由以下表示。
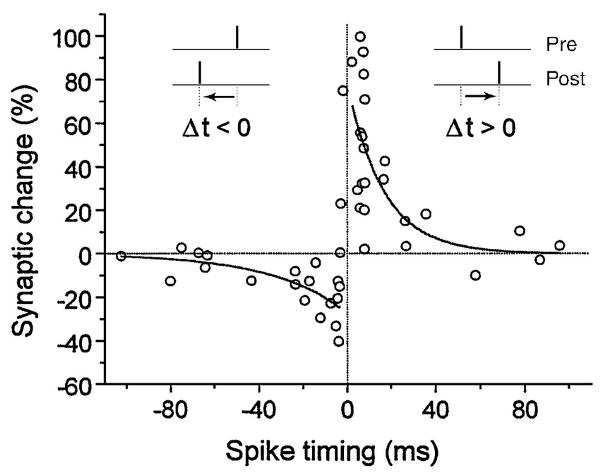
但我們今天不談STDP。我談的是(我唯一看得懂?)的SpikeProp。
目前能做到SNN監督式學習的演算法,除了SpikeProp之外、還有我一直非常好奇的ReSuMe(Remote Supervision Method)。SpikeProp用的方法是類似一般NN使用的倒傳遞(Back propagation,簡稱BP)。原理跟BP一樣,都是透過連鎖率從輸出層逐步偏微分至輸入層,因此如果看過BP會對SpikeProp的數學推導感到容易上手。
相反的,ReSuMe用的則是監督式的STDP,這個方法看起來很有潛力,不過暫且不提,畢竟我們得驗證其真實性。
- ReSuMe可能有潛力的原因:SpikeProp本身訓練方式還是NN舊有的倒傳遞、沒有耳目一新的算法,相反的STDP這種新方法是基於SNN而發展出來的,但大多還是用在非監督,因此ReSuMe竟然能改成用在監督,如果能驗證算法的正確性,我覺得我會傾向用ReSuMe
使用Multi-SpikeProp的SNN架構
現在我們做一些前置的定義,方便我們了解使用SpikeProp演算法時、SNN應該具備哪些特性。很多演算法常常會有一些很奇怪的前置設定,看起來似乎非常沒有道理,但這些都是每個作者為了自圓其說、或是讓結果能不要太難看所設定的。 理論上,一個好的演算法不應該存在太多不必要的前置條件,因為這樣就不符合通用(general)的特性。 但SpikeProp發展至今、許多人改良其算法、甚至已經發展出Multi-SpikeProp,因此定義會稍微有些不同,但概念都是一樣的:
1.在SpikeProp中,每次訓練一個epoch,輸出層跟隱藏層每顆neuron被限制只能發一次spike。Multi-SpikeProp只有輸出層被限制只能有一個spike,隱藏層則不受發spike次數的限制。這是唯一SNN當中聽起來不太符合生物學上定義的特性。由於SpikeProp算法上本質上用的還是倒傳遞,且 輸出形式基於的理論是Time-to-first-spike ,也就是我們關注的是第一個spike出現的時間,後面發出的spike我們一概認為不帶任何資訊。需要計算輸出層的損失函數,因此為了簡化誤差的計算量,我們只考慮輸出層的第一個spike
2.SNN網路內都是全連接層。我們先定義最後一層(輸出層)是第1層、層編號由後向前遞增。所以第L層所有neuron都會連接到前一層(第L+1層)的每個neuron
3.第L層neuron編號為j,從1到N L。K是突觸的數量,且每個neuron間的K都是一樣的。W ij 表示從前一層第i顆neuron、到後一層第j顆neuron之間的第k個權重。
4.假設前突觸第i號neuron在時間t i發出spike、且第k個突觸會造成d k延遲,則第k個突觸會在時間+d k將spike傳遞到後突觸neuron。
5.突觸的延遲參數對每兩個neuron都是一樣的、且每兩neuron間的第k個突觸都有相同的delay。
6.從同一個neuron發出的spike編號稱為g,總共有G j 個spike被發出
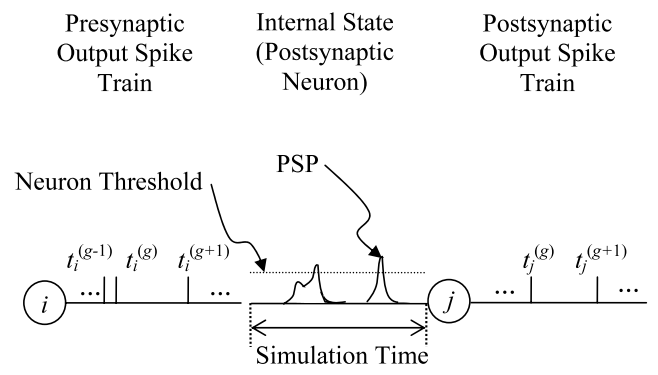
7.每顆neuron都會產生相對應的膜電位矩陣,我們稱為x,並以下標j、時間t表示第幾個neuron的膜電位、在時間t時的電壓,我們往後稱膜電位矩陣為內部狀態(internel state),也就是SNN網路中擁有「記憶」的部分。
跟許多RNN一樣,SNN由於擁有記憶的特性可用來處理時間序列的問題。RNN擁有記憶的方法是把上一個時間點的輸出做為下一個時間點的輸入,LSTM是在網路中保有長時記憶與短時記憶兩種輸入。但這兩種都不夠仿生,畢竟生物體可沒有這麼人為定義數學化的結構,而這也是SNN所追求的。SNN回歸最簡單直覺的生物體特性,也就是只要膜電位達到一定數值就會觸發的特性,以此作為記憶單元,避免了一般神經網路活化函數連小數值都能觸發的弊病,達到符合神經元傳遞訊息全有全無的仿生效果。但缺點也顯而易見,由於全有全無導致的微分困難,在網路訓練上會存在困難點。
neuron的內部狀態關係式
為了方便寫出式子,在這邊我們統整我們需要的幾個變數。並以以下圖示表示:
- 網路層數L,編號為小寫l,從1到L
- 神經元數Nl,編號小寫l從1到L,代表該層有Nl個神經元
- 前突觸神經元i,編號從i=1到i=Nl+1
- 後突觸神經元j,編號從j=1到j=Nl
- 突觸數量K,編號為小寫k,從1到K
- 連接前神經元i與後神經元j的權重為wijk
- spike觸發數量G,編號為小寫g,從1到Gj
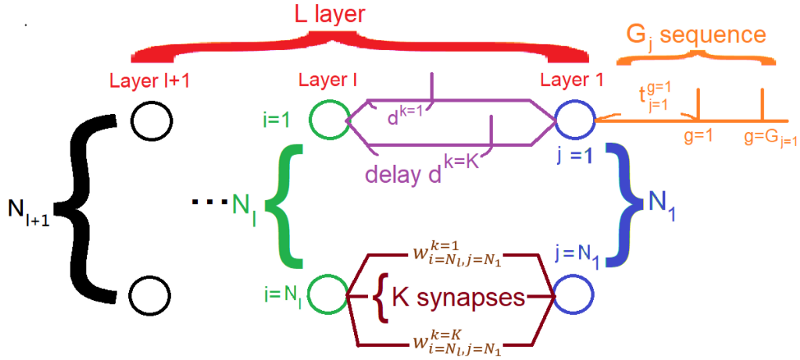
我們了解到,位於下一層l第j顆神經元的膜電壓,是由 「從1到第Nl+1個神經元」當中「第1到第K個突觸」的「第1到第Gj個spike」的EPSP、加上因為 「該神經元曾經被上一個spike觸發而造成不反應期」的IPSP 共同組成的。根據這個關係,「第l層的第j個neuron上」的膜電位電壓,在某時間t下的數值可以寫成以下式子:
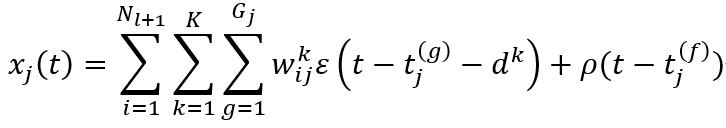
這個式子重要到不能在重要了,不一定要背起來,但看到一定要知道裡面參數的意義。其中epsilon可以使用不同的PSP函數。我們這邊使用的是alpha函數。
可以發現,如果該神經元j是第一次放出spike,表示沒有不反應期的發生,則後面那項rho函數就會消失掉,以此簡化該式。
SNN的損失函數
該SNN被限制最後一層的輸出只能發出一個spike,是為了方便進行倒傳遞演算。該研究算是早期的SNN研究,因此想法基本上無法跳脫倒傳遞的方式。而為了倒傳遞,此時必須定義一個loss function。由於輸出只會發出一個spike,因此 放出spike的時間點便成了我們要訓練的目標。此時我們希望SNN能訓練出一個能在指定時間點放出一個spike的網路。我們定義一個loss function E如下,並以常用於訓練神經網路的MSE均方差函數做為發想。其中t jd表示預期放出spike的時間點。
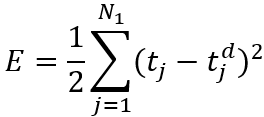
對神經網路有基礎的應該知道,我們應該讓整體網路的損失函數數值越低越好。因此,要找到損失函數的最低點,就必須對網路的權重與偏權值進行偏微分。這表示我們必須對該式子偏微分。由於該SNN沒有偏權值,因此我們只要對w微分即可。
輸出層的連鎖律拆解
由於損失函數當中看不到w變數,因此我們透過連鎖律拆解。總共拆成三個部分,分別是:
- 「Loss function E」對「實際放出spike的時間點tj」偏微分
- 「實際放出spike的時間點tj」對「輸出層內部狀態關係式xj(tj)」偏微分
- 「輸出層內部狀態關係式xj(tj)」對「輸出層權重wijk」偏微分
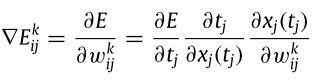
其中第一項展開後如下,很直覺:
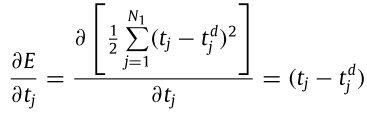
第三項展開後如下:
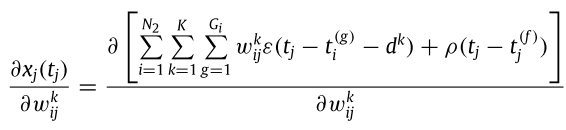
這裡有兩個省略的要點:
- 由於我們現在算的是最後一層的損失函數,而先前規定最後一層只會發一個spike,因此不存在不反應期,所以後面的rho函數可以直接去除
- 由於現在是對wijk微分,也就是「後面第j顆連接到前面第i顆的第k個突觸」進行微分,由於前面神經元每個突觸之間的權重不受彼此影響,表示不同突觸的權重彼此獨立、微分時不會互相影響,因此i跟k的summation消失
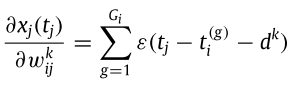
唯一比較麻煩的是第二項。 原因是「實際放出spike的時間點tj」是一個離散的數值,而非一個連續的可微分函數,因此無法直接對「內部狀態關係式x j(t j)」偏微分。這下尷尬了。幸好有人想出了替代方法:既然無法讓t j對x j(t j)直接微分,不如我們倒過來,「假設」x j(t j)對t j 可微,然後將其倒數。本篇作者有鑑於前一篇作者講得不清不楚(很多論文都是如此),他想出了更直覺的解釋方法。
首先我們知道x j(t j)是內部狀態函數,也就是膜電位。原本的思路是,我們要用「放出spike的時間點」對膜電位微分。但我們早就知道膜電位本身就是連續函數,這讓我們燃起了「是否能用膜電位來微分放出spike的時間點」的想法,畢竟,兩個變數只是分子分母顛倒而已。接下來,我們考慮一個膜電位隨時間變化的圖。我們也會引入theta參數,也就是放出spike的threshold,並用這個參數來偷梁換柱。
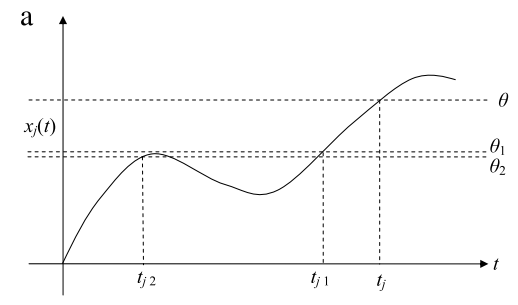
由上圖得知,當膜電位x在時間點t j超過了theta的門檻時,就會放出一個spike。原本theta只是一個跟膜電位無關的常數,但我們可以發現一個現象,就是當膜電位的圖不變,而theta的值下降的時候,放出spike的時間點t j就會往前移動。這很合理,當門檻變低了,spike放出時間也就提早了。 這時我們就想,是否可以把「膜電位x對tj的關係」轉換成「threshold對tj的關係」?因為圖上面的每個點(t,x j(t))都可以被(t j,theta)取代。這時,我們把theta想像成了一個可微分的變數了。由上圖得知,當threshold從theta降到theta 1時,threshold對t j的關係還是連續的。但當threshold從theta 1降到theta 2時,由於剛好放出spike的時間大幅提早,因此出現一個無法微分的斷層,如下圖所示,該theta被稱為theta jump 。
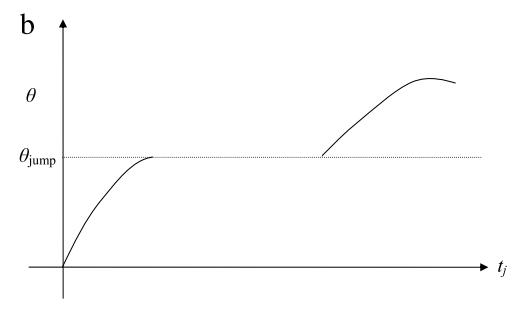
這下似乎又遇到了瓶頸,這意味著我們必須限制theta不能靠近theta jump才能讓微分成立。幸好這樣的假設不是空穴來風,我們根據前人訓練神經網路的結果知道,只要小心選擇網路的學習速率,就可以避免損失函數曲面上的誤差跳躍情形。也就是說,只要t j 只在該數值附近移動,就可以確保微分成立,代表我們把膜電位換成theta的假設是成立的。基於圖a與b的式子斜率相同,等同於以下式子成立:
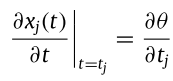
由於我們的最後目標是讓t j在分子,因此我們把右式改造一下,式子的意思是:門檻稍微變高(低)、放出時間稍微變晚(早)、反之亦然。這邊假設t j 的變化量極小,式子就能成立。
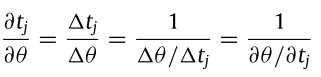
另外,我們知道要達成「延後放出spike的時間t j 」的目標,有兩種做法可以達成:
- 膜電位xj(tj)下降,讓膜電位累積電壓久一點才能超過門檻
- threshold的theta上升,門檻變高自然會晚放出
我們發現這兩者是呈反向關係,因此可寫出以下式子:
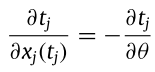
把以上三式子合併可得到
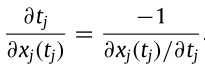
且該式子分母的算法如下:
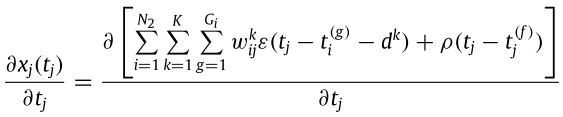
這跟之前某個式子差在之前是對權重微分,現在是對時間t j 微分,同樣有幾個原則可對該式子做簡化:
- 算的是最後一層的損失函數,因此不存在不反應期,後面的rho函數直接去除
- 由於每個突觸之間的spike delay時間不受彼此影響,表示不同突觸的delay彼此獨立、微分時不會互相影響,因此i、k、g的summation可以移到外面去
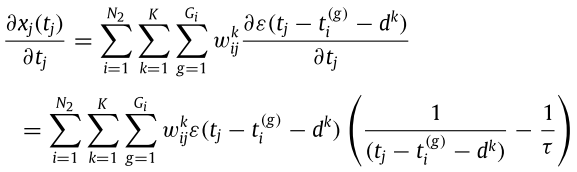
最後代回原式:
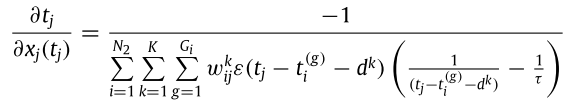
隱藏層的連鎖律拆解
看了這麼多公式,應該蠻累的了。但上面還只是最後一層的倒傳遞而已。最複雜的其實是「隱藏層」的倒傳遞。我們接下來要改變的是輸出層前一層的權重,也就是層數l=2的權重。我們同樣以最後一層的損失函數為基底,並將該損失函數對l=2層的權重進行微分。將式子拆成兩部分,分別是:
- 「Loss function E」對「l=2層實際放出spike的時間點tig」偏微分
- 「l=2層實際放出spike的時間點tig」對「l=2層的權重whik」偏微分
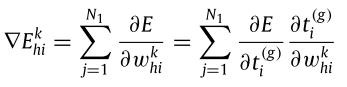
我們先關注前面「Loss function E」對「l=2層實際放出spike的時間點t i 」偏微分這部份,將式子用連鎖律展開,三部分如下:
- 「Loss function E」對「輸出層實際放出spike的時間點tj」偏微分
- 「輸出層實際放出spike的時間點tj」對「輸出層內部狀態關係式xj(tj)」偏微分
- 「輸出層內部狀態關係式xj(tj)」對「l=2層實際放出spike的時間點tig」偏微分
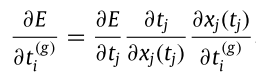
前面兩項很湊巧在前面都算過了,因此可以重複利用。而第三項的式子如下:
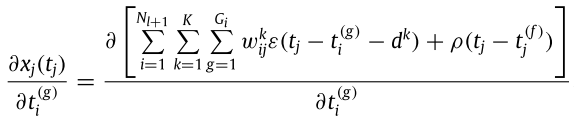
這裡同樣有兩個省略要點:
- 由於我們是對「l=2層實際放出spike的時間點tig」偏微分,而rho函數中的tj表示的是輸出層的不反應期函數,兩者獨立不相關,因此rho整項可消去。
- 同一層不同神經元的輸出不會互相影響,因此i的summation消失
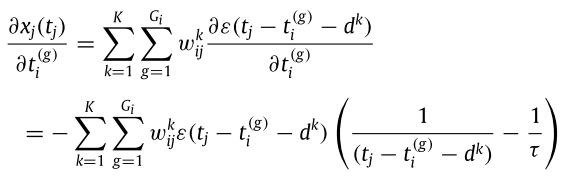
接下來是後面「l=2層實際放出spike的時間點t ig」對「l=2層的權重w hik」偏微分這部分。這部分比較特別,由於中間隱藏層就不再限制spike只能觸發一次,因此需要考慮隱藏層所有spike觸發的時間點,並從最後一個觸發的spike、到第一個觸發的spike的偏微分都要算。主要就是不斷重複利用先前的計算結果,只能說計算量真的很龐大。
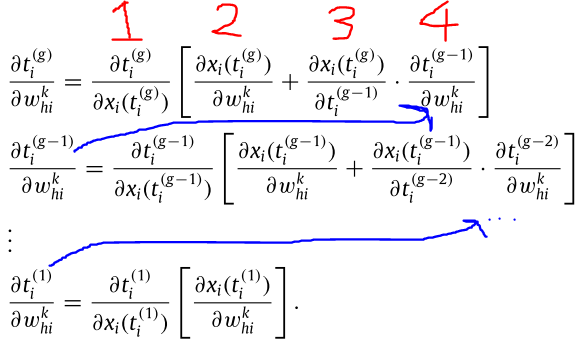
編號為1的式子(「l=2層實際放出spike的時間點t ig」對「l=2層內部狀態關係式x i(t ig)」偏微分)計算如下:
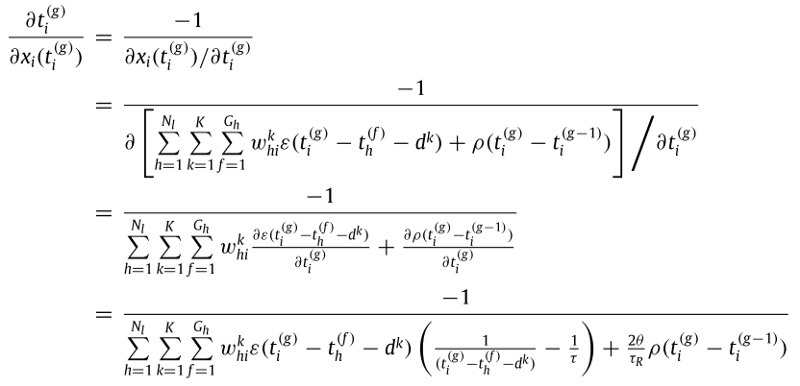
編號為2的式子(「l=2層內部狀態關係式xi(tig)」對「l=2層的權重whik」偏微分)計算如下:
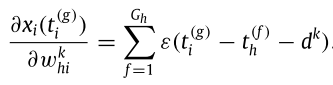
編號為3的式子(「l=2層內部狀態關係式x i(t ig)」對「l=2層實際放出spike的時間點t ig-1」偏微分)。請注意,之前都是對編號g的spike做微分,只有這一項是對編號 g-1 的spike時間點作微分,之後會不斷利用這個參數,從編號g算到編號1造成的影響。計算如下:
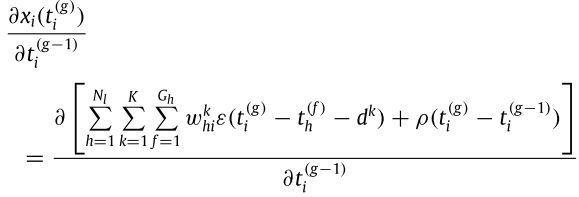
由於前一個觸發的spike時間與目前這個觸發的spike無關,所以反而只剩下後面不反應期那項。編號3式子最後簡化如下:
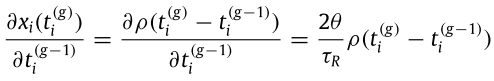
寫完之後,至少該交代的都交代完了,應該不用再淌這個渾水了。
Reference: A new supervised learning algorithm for multiple spiking neural networks with
application in epilepsy and seizure detection(2009)
Originally published at http://smilemirror.wordpress.com on January 28, 2021.
