狂徒書評 小資族累積資產的最快路徑 YP《一年投資5分鐘》

如果有人宣稱，他找到一個絕對賺錢的投資方法，那他就是騙徒。
但是如果有人認為，他的方式有超過95%的賺錢機率，而且還寫成幾百頁的書，拿出歷史紀錄和理論供大家檢視，那或許各位可以看看他的內容。

我平時比較少讀台灣的書，尤其關於「指數投資」領域。
事實上，大家在網路上已經能找到大部分的相關知識，所以沒必要額外買書。
如果妳只是想機械化執行指數投資，甚至連背景知識都不需要具備。

然而，我還是買書了。
我不但買書，我還寫書評。
寫書評之外，我也寫信和作者「YP」交流，為什麼?
是怎樣的場合，讓我想在推薦書的同時，還去踢館討教? 他又有什麼回應?

有天我和理財館長(指數投資創作者)閒聊。

「YP最近出一本書，你看過嗎?」
「沒有，我很少在看台灣的書。」
「我覺得他寫得很好，你可以找來看。」
「那有時間我會買來讀。」

就這樣，出版不到三周，我已經讀完了。

內容部分，YP提到保險、緊急預備金和開戶層面，當然資產配置、選股擇時這些經典指數投資因素也不會少。
我可以感受到他想要照顧新手的用心，但同時也欣賞他將理論解釋清楚的寫作功力。

對於想進一步驗證的讀者來說，書中有清晰的圖表輔助說明，而書末的「文獻」也是很重要的橋梁。
相信有些人本來就喜歡讀不同paper，所以不覺得這些內容有多難。
但考慮到作者瞄準的群眾，《一年投資5分鐘》能夠拉出很大的跨度，讓指數投資的新手真正學到知識，這就是本書厲害之處。

放眼全台灣的投資理財創作領域，YP算是我非常欣賞的作者。
我不會為了介紹一個作者，而去貶低其它人，但這個領域確實存在著烏合之眾，就像社會上自然有上下階級，不是每個人都能達到「優秀」的高度。
我就是因為了解指數投資的常見議題，所以我知道哪些作者在教育民眾，哪些作者只是藉此牟利。

每個人都會說「4%法則」，但有多少作者知道背後原因?
「股債結合」很好，好在哪裡? 比例怎麼算?
大家都聽過「分散投資」，那背後又有什麼意義?

我可以輕易寫出讓普通讀者看不懂的文章，我不在乎我影響多少人，因為我是投資人，只對自己的資產負責。
所以我也認為，把困難的理論轉化成淺顯易懂的概念，是身為投資理財作者的目標，而YP做得很好。

舉個例子，我常常用「定投」來檢視一個作者的知識水準。
我寫過單筆投入勝過分批定投的文章，所以我也很清楚檯面上作者的思路。
他是跟著網路風向走，還是逆風堅持自己的觀點?
他是引用別人的結論，還是自己拿數據出來研究?
在這些背景下，作者的網路文章讓我驚喜。

知道真相是一回事，傳播真相又是另一回事。
我認為YP在類比、檢驗和資料蒐集的能力，達到出眾的境界。
所以，聽到他出書，我就直接買來看了。

事後證明，YP對於知識的追求非常積極，而且也對自己的著作負責。
作者不但回覆我的信件，還傳了「勘誤表」給我，正好顯示了他持續修正和精進的態度。
如果各位讀者有興趣，也可以寫信給他或遠流出版社。

嚴格來說，這本書適合所有人，因為指數投資本來就有此優勢。
然而我特別推薦想要快速累積資產的小資族，至少看過YP的書。

我贊同作者的說法，專注於本業賺取主動收入，再利用指數投資和資產配置讓財富加速累積。
換句話說，我們要是沒錢，就努力賺錢、讓錢滾錢，而不是把精力花在和市場對抗。
他自己就是利用這種方式，邁向8位數存款，而且每年只花5分鐘操作。

因此，如果各位想要開始投資，或是想了解指數投資，那麼這本書是很好的入門讀物。

書評部分到此結束。
如果你想買書，可以到各大網路平台。
一年投資5分鐘：打造每月3萬被動收入，免看盤、不選股的最強小資理財法

如果妳想繼續看我和YP的信，就不要轉台。

好了，既然我這麼推薦作者YP和《一年投資5分鐘》，那我幹嘛還寫信去「吵架」?
因為我是讀者，我也是認同他的投資人。
我越欣賞一個人，就對他越嚴格，因為我知道對方經得起檢驗。

我根本不認識YP，而且論資歷和年紀，我都是晚輩。
但是我沒在怕，我也知道他不怕。
當一個作者足夠強大，他就有本事針對議題討論，而不是閃避或反射性的批評。

我在書中看到，他拿出「正偏態」來說明「市場報酬能戰勝大部分的投資人」，這讓我非常好奇。

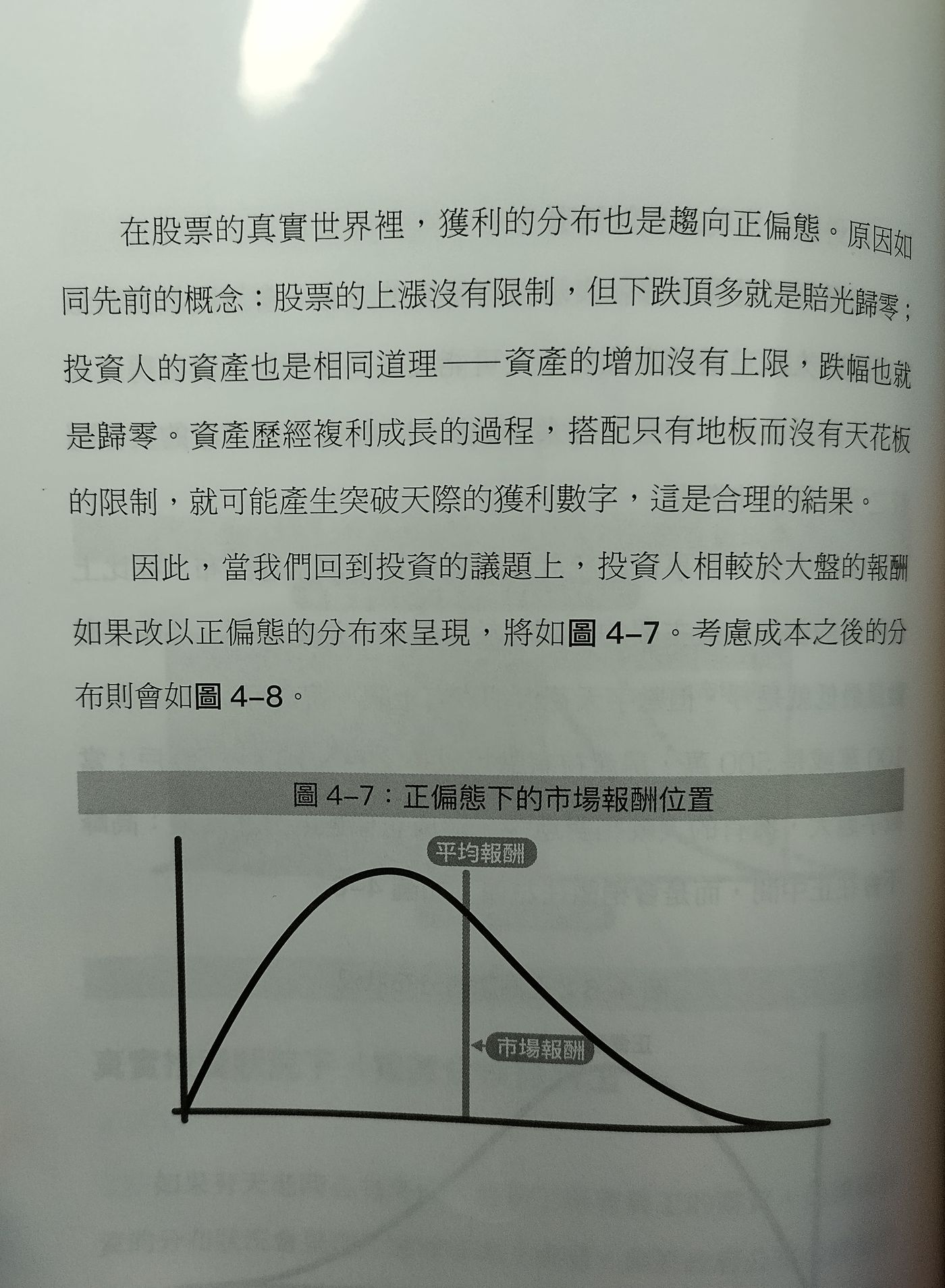
首先，股票價格確實有可能突破天際，但幾乎不可能變成負數，所以股價可以有非常高的預期報酬。
然而，並非每個人都完全跟隨股價漲跌，所以投資人各自拿到的「報酬」，有可能變成負的。
我認為從價格特性去推論股東報酬分布，是不嚴謹的思路。

再者，我判斷書中股東報酬分布的型態，應該是YP的自行猜測。
雖然我喜歡結論本身，但是在書中我並沒有看到「證據」。
因此我也想知道，偏態圖形到底來自哪篇文獻，或是哪些原始數據。

還有一點，YP在相關文章提到用均值、中位數和眾數來判斷偏態。
他認為「正偏態表示平均數大於中位數(中間的位置)與眾數(隨機取樣最可能的結果)」，但此定義有誤。
我不從數學角度切入，而是隨手寫了一組「反例」給他，說明正偏態分布中，依然有均值小於中位數的情形。
套用回書中的內容，即使投資人報酬分布是正偏，還是可能讓「多數人都打敗大盤」。

12小時內，YP迅速回信給我。

他證實我的猜測，由於投資人的報酬難以被統計，所以他並沒有充足的文獻和數據來源佐證。
然而YP也認為，正偏態的假設合理。
因為股價的漲跌幅有下限而無上限，所以長期累積下來，投資人的資產有虧損極限，頂多歸零。
他進而推論市場上可能的獲利分布，屬於正偏態。

同時我也得知，基於YP對正偏態的研究，他採取的定義就是「平均數大於中位數」。
而針對我提出的反例，他也使用「離散違規」來描述，並引用文獻Mean, Median, and Skew: Correcting a Textbook Rule.
不過YP也表示，既然反例存在，那原定義就不完美。

另外，雖然對於偏態的定義，會導致指數投資和眾人報酬對比的推論，出現瑕疵，但是我也沒有證據說明，所謂例外會存在於真實世界的報酬。
因此，總體而言，雖然推論過程和定義存在漏洞，但是主要結論依然不變。

還有個好消息，就是他寄了一份勘誤表。
收到這個禮物，我覺得非常開心。

既然如此，我再次回信過去。

我重申定義精確的必要性，尤其是報酬和分布，會涉及到時間長短、大盤或個股、橫截面或時序分析，造成偏態的意義不同。
我提到了選擇權BSM定價模型的log normal, Wealth Creation in the U.S. Public Stock Markets 1926 to 2019, Skewness in Stock Returns: Reconciling the Evidence on Firm Versus Aggregate Returns 和 The Skewness of the Stock Market over Long Horizons.
分別討論考慮短時漲跌合理性的偏態、長時間橫截面對比、時序分析下對於正負偏度的解釋以及時間窗口造成偏度轉負且衰退趨緩的特性。
我也區分上述統計對象，認為不能直接從股價特性推到股東報酬，再推到資產變化。

至於Mean, Median, and Skew: Correcting a Textbook Rule, 確實提到離散違規。
然而文獻中也提到，正偏態下均值小於中位數，包括離散、多峰分布和一邊長尾一邊重尾的分布......等可能。
YP直接把均值和中位數的關係，定義為偏態的方向，不過我自己的學習過程是用三階動差來看待偏態/偏度，所以事實上這兩個定義並不等價。
因此，同一「單峰連續」分布，有可能在兩個定義中分別為正偏和負偏。
我認為推論上，他不能用離散違規來否定我的反駁，況且股價和回報本身，正是被當成連續分布的離散。

對於推論過程，如果YP先假設回報呈現正偏，而且認為假設合理，同時也相信正偏等價於「均值大於中位數」，所以推論出指數投資能戰勝多數人，那就屬於「竊取論點」。
也就是說，如果有人假設回報呈現負偏，那他也可能照樣推出完全相反的結論，而且他也可以說「相信在此假設下，大部分的情況會如期呈現。」
因此，如果今天出現某個作者宣稱，報酬呈現負偏態，而且指數投資輸給大部分的人，那我們也沒有討論的施力點。

同時，我也在想解套方案，在不影響正確性和嚴謹性的前提下，得到簡單有力的結論。
我認為繞過偏態的定義差異，直接描述中位數和均值的關係，也可以達到目的。
或者拿到原始數據，根本不需要用模型和推論工具。
當然在現階段，或許加強合理性和間接證據，會是提升說服力的權宜之計。

討論至此，我們愉快結束話題。(對話經模糊化處理)
不過YP也很夠意思，他又送我一本附帶「簽名」的書。
而這對我而言，具有很強的意義。

我是因為作者的素質而買書，幾經交鋒後，他也證明了自己的實力和我的眼光。
雖然我確實質疑YP的論點，但他理性認真討論，也讓我有對於指數投資更深的了解，以及對於數學和統計等文獻的涉獵。
身為偶而分享文章的業餘投資人，找到一位值得學習交流的對象，這種快樂大概只有喜歡「挑戰」的人才知道。