关于机器学习:概述
本质上是部分简明神经网络教程(微软俱乐部整的)的笔记(逃
你有一个模型——或许它不是完美的(这不是铁定嘛)反正它已经是这样了——你可以拿他来做一些预测或者分类些什么,这是你的目的。于是你扔去了一个数值之类的到模型里面——初始化——于是这个你扔进去的玩意就开始在模型里面向前计算,最后得到了一个数值,正巧的是:你知道你扔进去的那个玩意所对应的正确值——显然和模型算出的结果有差距(损失),于是你让这个损失值返回模型让它反向计算对模型进行微调来使模型更趋近于完美——这就是机器学习的过程
举个栗子
目的:猜到乙心中的数字;
初始化:甲猜5;
前向计算:甲每次猜的新数字;
损失函数:乙在根据甲猜的数来和自己心中想的数做比较,得出“大了”或“小了”的结论;
反向传播:乙告诉甲“小了”、“大了”;
梯度下降:甲根据乙的反馈中的含义自行调整下一轮的猜测值。
这里的损失函数是什么呢?就是“太小了”,“有点儿大”,很不精确!这个“所谓的”损失函数给出了两个信息:
1.方向:大了或小了
- 2.程度:“太”,“有点儿”,但是很模糊
- or 黑盒
- 目的:猜到一个输入值,使得黑盒子的输出是4;
- 初始化:输入1;
- 前向计算:黑盒子内部的数学逻辑;
- 损失函数:在输出端,用输出值减4;
- 反向传播:告诉猜数的人差值,包括正负号和值;
- 梯度下降:在输入端,根据正负号和值,确定下一次的猜测值。
- 搭建一个神经网络,给出初始权重值,我们先假设这个黑盒子的逻辑是:z=x+x2;
- 输入1,根据 z=x+x2 得到输出为2,而实际的输出值是2.21,则误差值为 2−2.21=−0.21,小了;
- 调整权重值,比如 z=1.5x+x2,再输入1.1,得到的输出为2.86,实际输出为2.431,则误差值为 2.86−2.431=0.429,大了;
- 调整权重值,比如 z=1.2x+x2,再输入1.2……
调整权重值,再输入2……
如果误差值是正数,我们就把权重降低一些;如果误差值为负数,则升高权重
- 所有样本遍历一遍,计算平均的损失函数值;
- 依此类推,重复3,4,5,6过程,直到损失函数值小于一个指标,比如 0.001,我们就可以认为网络训练完毕,黑盒子“破解”了,实际是被复制了,因为神经网络并不能得到黑盒子里的真实函数体,而只是近似模拟。
或者举个打靶的栗子
- 目的:打中靶心;
- 初始化:随便打一枪,能上靶就行,但是要记住当时的步枪的姿态;
- 前向计算:让子弹飞一会儿,击中靶子;
损失函数:环数,偏离角度
这里的损失函数也有两个信息:距离 and 方向——所以,梯度,是个矢量! 它应该即告诉我们方向,又告诉我们数值。
- 反向传播:把靶子拉回来看;
- 梯度下降:根据本次的偏差,调整步枪的射击角度。
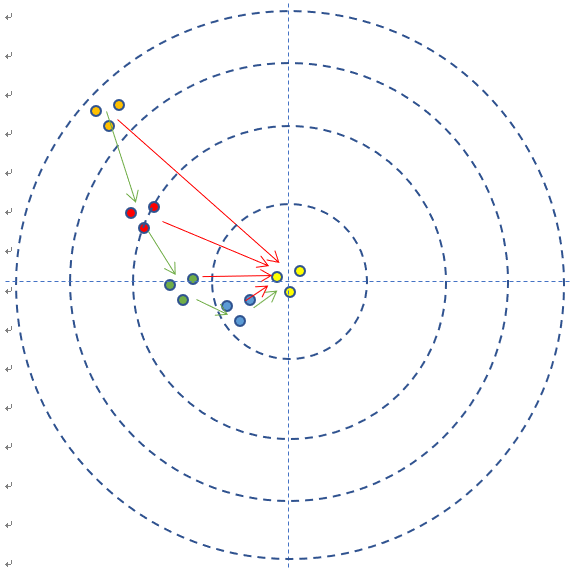
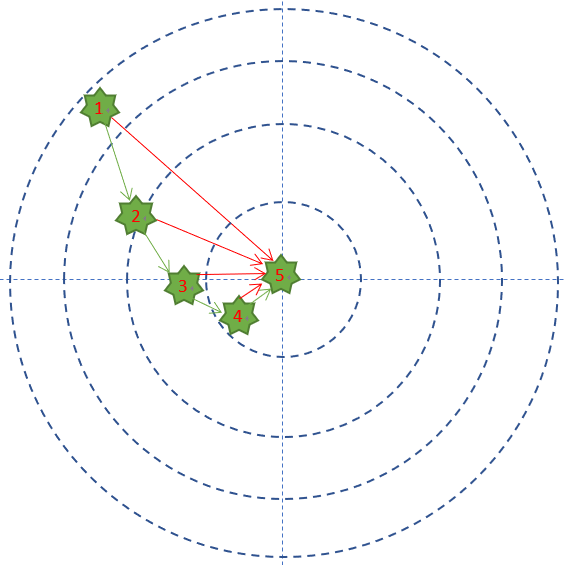
- 每次试枪弹着点和靶心之间的差距就叫做误差,可以用一个误差函数来表示,比如差距的绝对值,如图中的红色线。
- 一共试枪5次,就是迭代/训练了5次的过程 。
- 每次试枪后,把靶子拉回来看弹着点,然后调整下一次的射击角度的过程,叫做反向传播。注意,把靶子拉回来看和跑到靶子前面去看有本质的区别,后者容易有生命危险,因为还有别的射击者。一个不恰当的比喻是,在数学概念中,人跑到靶子前面去看,叫做正向微分;把靶子拉回来看,叫做反向微分。
- 每次调整角度的数值和方向,叫做梯度。比如向右侧调整1毫米,或者向左下方调整2毫米。如图中的绿色矢量线。
- 在本例中,多个样本可以描述为连发射击,假设一次可以连打3发子弹(好家伙直接霰 弹),每次的离散程度都类似
- 如果每次3发子弹连发,这3发子弹的弹着点和靶心之间的差距之和再除以3,叫做损失,可以用损失函数来表示——在这个例子里面,用得分来衡量的话,就是说小明得到的反馈结果从差9分,到差8分,到差2分,到差1分,到差0分,这就是用一种量化的结果来表示小明的射击结果和目标之间差距的方式。也就是误差函数的作用。因为是一次只有一个样本,所以这里采用的是误差函数的称呼。如果一次有多个样本,就要叫做损失函数了。
其实射击还不这么简单,如果是远距离狙击,还要考虑空气阻力和风速,在神经网络里,空气阻力和风速可以对应到隐藏层的概念上。
- 简单总结一下反向传播与梯度下降的基本工作原理:
- 初始化;
- 正向计算;
- 损失函数为我们提供了计算损失的方法;
- 梯度下降是在损失函数基础上向着损失最小的点靠近而指引了网络权重调整的方向;
- 反向传播把损失值反向传给神经网络的每一层,让每一层都根据损失值反向调整权重;
- Go to 2,直到精度足够好(比如损失函数值小于 0.001)。
简明的概述结束辣
以上
