報酬和波動的關係

「報酬和波動有什麼關係呢?」
狂徒邊想邊走,來到一處峽谷。
正想先休息,旁邊突然跳出來一個人。
「你是......」狂徒握了握刀柄。
「我是PTT正二王,筆名林大仁。」
「喔! 原來你就是那位轟動武林的作者啊? 聽說明年要出槓桿ETF的書,真是幸會。我是狂徒。」
「什麼武林? 聽起來像是別派長老。我的內容和五零比較有關,包括0050正二。」
「那你是賺錢大師嗎? 我最近對波動有興趣。」狂徒說。
「投資要靠自己,不過我可以和你說點槓桿ETF的性質,也和波動息息相關。」大仁笑了。
說完,大仁拿給狂徒兩本書,分別是Richard Ferri "All About Asset Allocation"和 Mark Spitznagel "Safe Haven". (資產配置投資策略/黑天鵝策略)
「這些書都提到波動率、幾何平均報酬和算術平均報酬。如果算術平均回報相同的話,那波動率越大,幾何報酬就會越小。」
「所以這意味著什麼?」
「這代表,我們應該在算術平均一樣的前提下,盡量減少波動率,可以讓複利效果變好。而且對於槓桿ETF而言,波動率變小的好處會更加明顯。」
這席話,讓狂徒心中少了大半疑慮。對於追求長期複利的人來說,投資策略風格應該偏向慢慢累積、成長,而不是大起大落,這樣速度反而快。
又經過一番對談,狂徒告別正二王大仁,繼續動身往山谷走去。
「狂人谷? 」狂徒看到路旁石碑。
「感覺這裡的人類應該會很好相處,就不知道有沒有歇腳的地方。」狂徒心想。
走了半個小時,狂徒找到前面一棟屋子,不過屋內人也發現了他。
「前面那位兄弟,拿金銀刀的,這麼晚經過狂人谷想做什麼?」
「我要去找賺錢大師。」狂徒回答。
「賺錢大師? 這裡沒有。不過天色已晚,再往前走很危險,你要不要先休息?」
「就等你這句話。」狂徒笑了。
狂徒走進屋中,發現還有四人正在喝酒。
「我是狂徒。」
「巧了,我們是狂董、狂爺、小狂和狂犬,所以這裡叫狂人谷。」
經過寒暄,狂徒提到自己剛學到的波動率問題。
「喔,這個我懂,我舉個例子給你看。」狂董說完,畫了一張表。
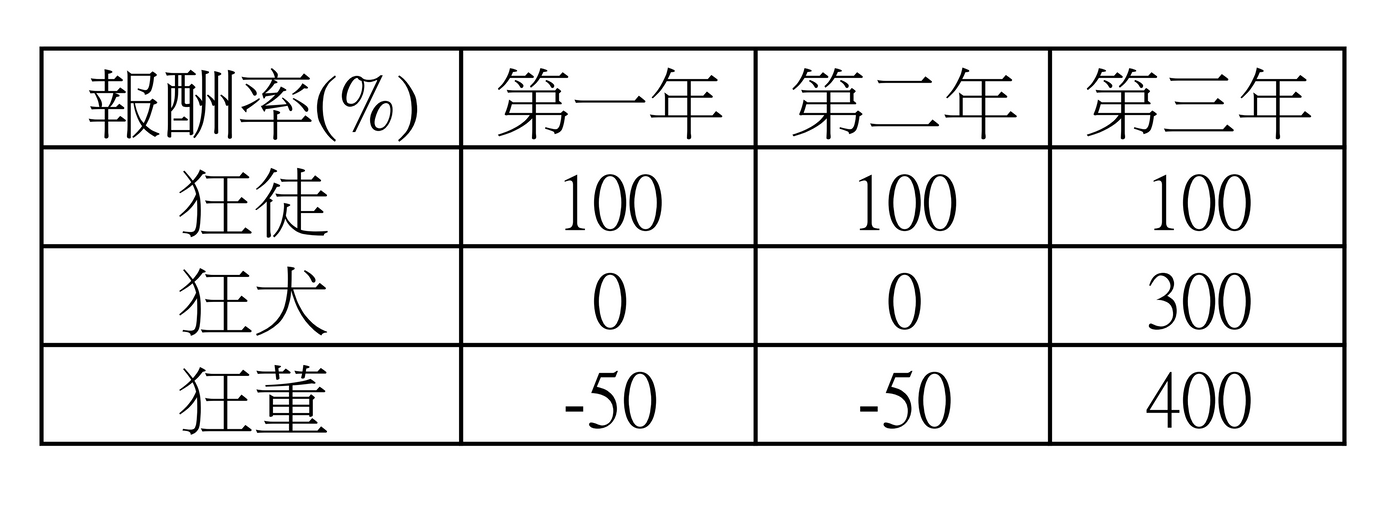
假設狂徒、狂犬和狂董都投入100萬元,而且算術平均報酬率都是100%
統計三人的績效,就會發現一件事情。
「波動越大,幾何平均報酬越差。」
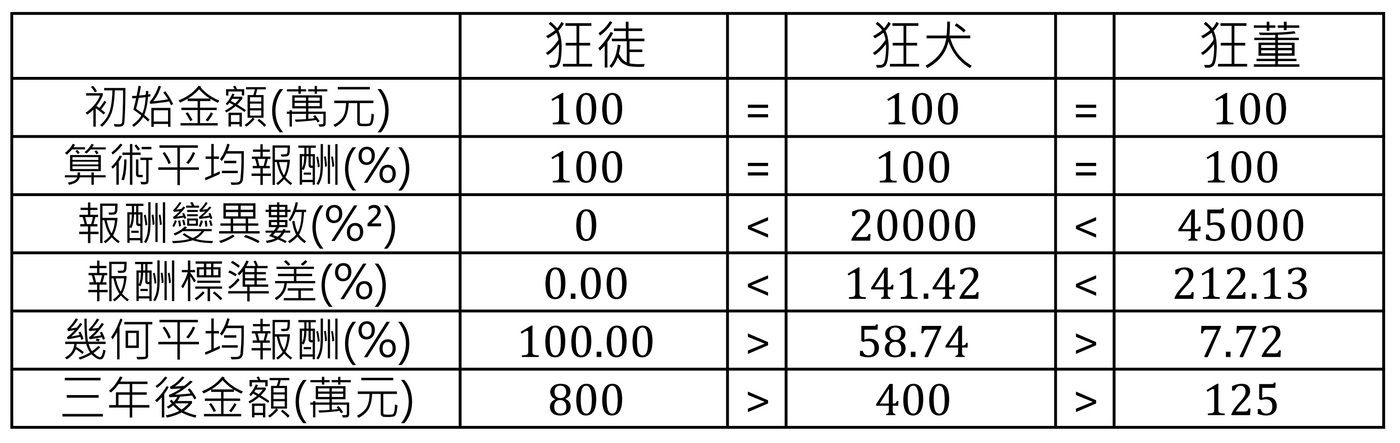
這呼應了林大仁的告誡和Richard Ferri的書本內容。
「原來如此,看來波動率也沒什麼秘密。」狂徒說。
「且慢,事情沒有這麼簡單。」一旁狂爺開口了,他又畫出另一張表格。
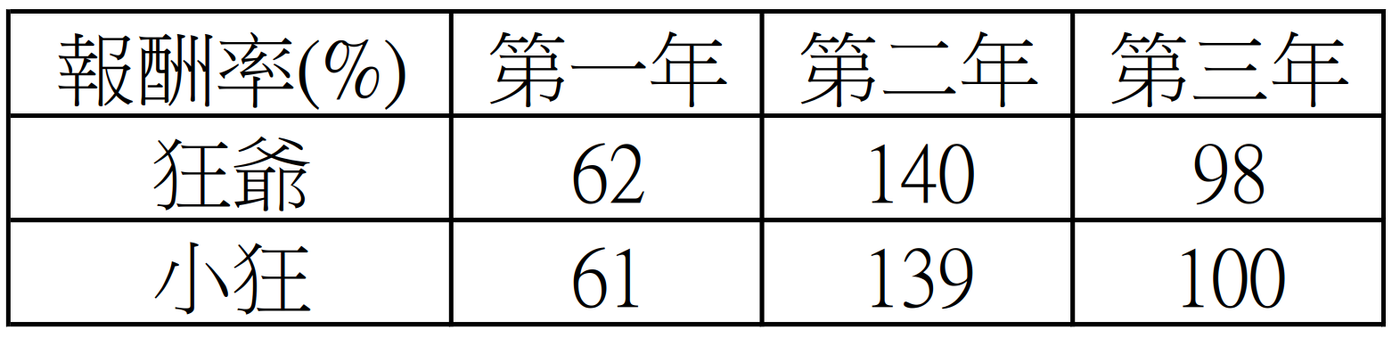
這次,狂爺和小狂的算術平均報酬依然是100%,也用100萬元進場。
可是雖然狂爺承受更大的報酬波動,卻仍拿到更高的總報酬和幾何平均報酬。(表格中小狂和狂爺互換。)
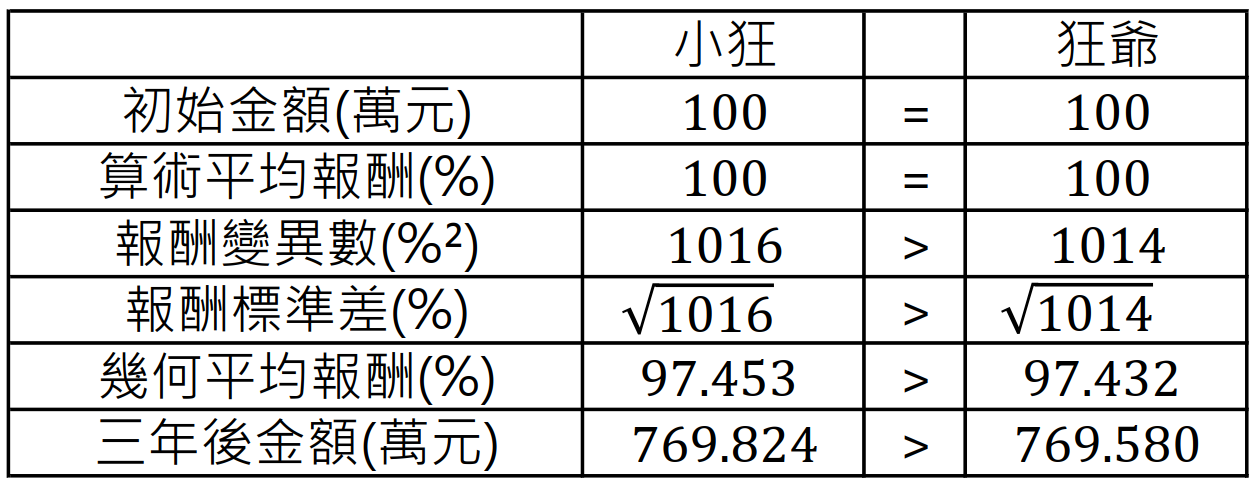
為什麼會這樣呢?
狂徒看傻眼,狂爺笑著開始解釋。
1. 壓縮資訊造成破壞
不論我們計算平均數還是標準差,都是把一堆數據簡化成一個數值,這當中我們損失了很多資訊。
這就像妳可以告訴我手機號碼最後一位是奇數還是偶數,大概花不到三秒鐘,可是光憑這個資訊我根本無法得知號碼本身。
因此,如果你手中有一組數據,那計算出幾何平均、算術平均和標準差,沒有難度。可是如果我只給你最終統計資訊,你沒辦法回推數據本身,也無法確認三者間的關聯。
簡單來說,「相同的算術平均報酬之下,波動越劇烈,複利累積效果越小」,推論根本不成立。
2. 常態分布假設錯誤
大家喜歡假設市場價格波動呈現常態分布,可是這違反了事實。無論是股票或商品,無論是單一標的或大盤,無論是報酬隨時間分布,還是成分股之間的報酬分布,全部都不是常態分布。
當我們說一個分布呈現常態分布時,其實暗示了數據們「很乖」,既沒有左右偏差,也沒有特殊的尾端事件。如此一來,我們可以僅憑少數資訊就回推數據分布,也可以得知平均值。一般而言,由於真實波動分布和常態相似,所以我們這樣使用並不會有問題。可是在特殊情況下,例如增加槓桿或拉長複利時間,兩者的差距會被放大,我們便不能忽略。
只能說,算術平均相同時,通常波動率越大,複利效果會越差,有人甚至推算出參考數值,不過這背後並沒有數學保證。
狂徒聽完後,喝了一碗酒,他好像聽懂了...
翌日,狂徒告別了狂人谷的幾位居民,再度踏上了旅程。
現在他腦中有個疑問。
「常常聽到高風險高報酬,那我投資到底要找大波動還是小的?」
註: 波動率系列寫起來真好玩XD
有機會繼續接,各位朋友若有疑問可以提出。
大仁就是這樣找到我的
https://www.facebook.com/CapMadX
參考:
