Github連結

YoYo~~今天想來幫自己記錄一下用來衡量機器學習-迴歸模型好壞的指標，所以這篇也是根據一些其他的教學文章來整理，並且互相補足，再融會成我自己的方式寫下的喔，我參考的教學文也都會放在底下供大家參考，其實是因為今天被突然問到模型報告裡的各項指標，所以特別學習的XD

動機 - 要如何知道我們訓練出來的迴歸模型好壞?

大家再訓練完模型後，第一個反映一定是想知道它的預測準確率(Accuracy)，也代表著這個模型的性能到底好不好，除了Accracy以外，當然還有很多非常精準且厲害的指標來幫助我們判斷模型的優劣，而我們如果要出去參加機器學習的比賽，評分的標準也幾乎都是用這幾個指標來評比，所以知己知彼百戰百勝，就像我們要知道出考卷的人是誰，才能更好的準備考試，這個舉例怪怪的XD，但就是這個意思

1. SSE (The sum of squares due to error) - 和方差、誤差平方和

• 計算方法: 擬和數據與實際數據的誤差平方和，也就是計算實際數據與模型擬和訓練集後的預測迴歸線，迴歸線上數據誤差的平方和，再乘以一個權重值
• 公式

• 筆記: SSE的值越接近於0越好，表示訓練出來的模型與數據的擬和度很高，當然預測能力也會越好

2. MSE (Meansquared error) - 均方差、方差

• 計算方法: 實際的數據資料值減掉模型的預測值，然後平方後，求總和，最後取平均值
• 成本函數(Cost Function): 其實與我之前的邏輯迴歸文章提到的成本函數(Cost Function)，或稱損失函數(Loss Function)是一樣的喔，我們的目標就是要最小化成本函數來找到最佳模型，類似於L1損失函數
• 公式

3. RMSE (Root Mean Squard Error) - 均方根誤差

• 實際的數據資料值減掉模型的預測值，然後平方後，求總和後，取平均值，最後再取根號
• 不就是MSE開根號?幹麻還特別需要它?

為了更好的描述資料，簡單來說就是有些數據資料的單位，可能是非常大的，像是企業要買機器設備，隨便都是億起跳的，那它的差值平方會超大，所以為了更好的說明我們訓練出來的模型效果，我們需要對這麼大的數值開根號，來把它的單位降的跟原本的單位一樣

• 公式

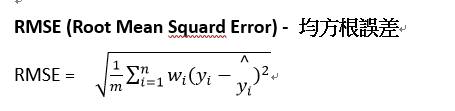
• 補充說明: MSE 與 RMSE的梯度是不一樣的，RMSE的梯度要比MSE的梯度多乘一個值，因此在使用梯度來優化模型時，需要調整學習率

4. R-square (Coefficientof determination) - 確定係數

• 解決的問題: 如果直接看其他的指標，每個指標都會計算出不同數值，很難從值看出模型表現的性能優劣，像是假設我們拿預測不同問題的計算結果: A,B，A = 2或6或8, B=0.4或0.6或0.8，然後我們要評比哪個模型好，但我們根本不知道怎樣算好
• 解決辦法: 這時候就需要拿模型與基準線比較來得知好多少，R-square是一個介於0~1的分數，可以想像成正確率的概念，越接近1越好，0當然就是最差的了，而所有的模型透過R-square都會被計算成0~1之間的分數，這樣就很方便比較囉
• 公式

• 補充SSR與SST的公式
• SSR(Sum of squares of the regression) : 模型的預測資料值與實際資料平均值之差的平方和

• SST(Total sum of squares): 實際資料值與實際資料平均值之差的平方和

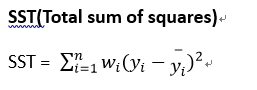
• 補充公式說明: SST = SSE + SSR

6. MAE (Mean absolute error) - 平均絕對誤差

• 計算方法: 計算模型的預測值與實際數據的目標值之間誤差，取絕對值後，再取平均
• 公式:

• 補充說明: MAE對異常值沒有那麼敏感，類似於L2損失函數，它的極小值點等於所有實際數據目標值的中值，不可微分，指的是當模型的預測值與實際數據的目標值相等時是沒有辦法計算的，只能用條件判斷來賦予它值
• 那要使用MAE還是MSE?
• MAE: 有異常值的情況，如果不想要這些異常值影響模型
• MSE: 有一點異常值的情況，如果想要含括這些異常值

7. MSPE(Mean square percentage error) & MAPE(Mean absolute percentage error)

• 說明: 當我們想要預測兩間不同的飲料店賣出多少杯飲料時(如下)，發現雖然都是多賣一杯，但是賣的數量單位可是差很多也，而因為MSE是計算絕對誤差，所以MSE卻是一樣的，這樣感覺不太公平吧!!所以就要使用MSPE與MAPE，它們會計算相對的誤差，在每個誤差項除以相對應的實際數據目標值來得到相對的誤差，也可以理解為MSE與MAE的加權指標

飲料店A: 預測98杯，實際99杯，MSE = 1
​
飲料店B: 預測999998，實際999999，MSE = 1

• 重點整理:
• MSE & MAE: 考慮的是絕對誤差
• MSPE & MAPE: 考慮的是相對誤差
• MSPE的極值: 實際數據目標值的加權平均值
• MAPE的極值: 實際數據目標值的加權中值
• 公式
• MSPE

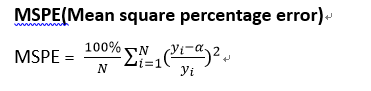
• MAPE

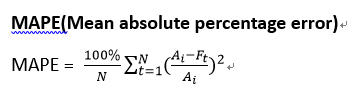
8. RMSLE (Root mean square logarithmic error)

• 說明: RMSLE就是對數(log)形式的RMSE，與MSPE & MAPE一樣考慮相對誤差，但它的誤差曲線具有不對稱性喔
• 公式

補充: 指標的關聯

• MSPE - 具有權重概念的MSE
• MAPE: 具有權重概念的MAE
• MSLE: 取對數(log)的MSE

Reference

https://www.youtube.com/watch?v=wrndkAJrqB0&feature=youtu.be

https://www.youtube.com/watch?v=9u-PR08kcE8&feature=youtu.be

https://www.youtube.com/watch?v=5z9xSUFisYs&feature=youtu.be

https://www.itread01.com/content/1546851440.html