随机数的惊人复杂性
本文翻译自 The Surprising Complexity of Randomness,原文作者:Brett Romero,2017 年 5 月 20 日。
之前,在一次不使用数据库创建一个简单应用的经历中,我接触到了随机性(randomness)。随机性和随机数生成是计算机科学领域一个非常艰深又重要的部分,但同时也是一个计算机科学领域之外鲜有人知的概念。因此,本着人人为我、我为人人的期望,我将在本文中谈谈随机性那惊人的复杂性(complexity)。
我们为什么需要随机性?
随机性有很多用途。但首先,需要强调一件事:当涉及计算机和计算机科学时,随机性通常是通过随机数体现的。随机排列的数字序列可以用于很多不同的目的,从简单随机播放音乐列表到更重要的为安全登录、数据加密生成随机密钥,还可以用在涉及大量金钱的在线赌博中进行随机洗牌。
如何生成随机数?
随机数有两种:伪随机数(pseudorandom numbers)和真随机数(true random numbers)。
伪随机数是指看起来像是随机产生的数,但却并不是真正随机的。通常来说,伪随机数是通过算法生成的。该算法可以基于用户或程序员提供的种子值(seed value)来生成一个新的数。这些算法一般的工作方式是取一个等式的余数——该等式包含了该种子值和若干大数。
举个例子,假设我们使用下面这个非常简单的等式来生成一些随机数:
R = (387 x S + 217) // 954
其中,R 是要生成的随机数;S 是 R 的种子值;// 表示模除法(modular division),其结果是该除法的余数
比如,如果种子值 S 为 43,那么该等式生成的第一个随机数就是:
R = (387 x 43 + 217) // 953 R = 657
将这个结果作为 S 再次插入原等式,就可以得到第二个随机数:
R = (387 x 657 + 217) // 953 R = 25
这个过程可以不断重复,从而得到一系列随机数。
虽然这个例子很简单,但这种将上一个随机数用于原等式以生成下一个随机数的过程几乎被用在了所有常见的伪随机数生成器中。而这个过程会导致两种属性,但都无关复杂性。
首先,如果种子值 S 是一样的,那么该算法所生成的随机数序列也将会一模一样。这意味着,如果你知道这个等式,并且知道种子值,那么你就可以预测整个「随机」数序列了。
其次,不管怎样,这个序列的模式最后都会重复。也就是说,这个等式会在某个时候生成之前曾经出现过的数字,然后后面的所有数字都会开始重复。而且如果等式和大数选择得不合适,这种重复可能会来得很快。
创建真随机数
那我们为什么还使用伪随机数呢?因为使用计算机生成真正随机的数实在太困难了!计算机在设计上就是要按照完全一样的方式执行一套指令,每次都得到确定的结果。正是这样的可预测能力才使得它们强大且高效。但也正因为此,可预测能力让真随机数生成变得非常复杂。
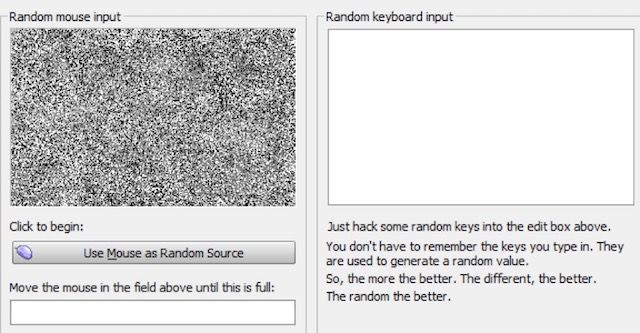
因此,为了让计算机能产生真正随机的数,它需要从一个真正随机的外部来源获取输入。这个外部输入可以是人类通过键盘或鼠标的操作,也可以是一个办公室环境中一个繁忙网络的网络活动情况。当然,也可以使用更加复杂的来源,比如大气瑞流对一束激光的影响或放射性同位素的衰变情况。
为什么这很重要?
伪随机数和真随机数之间的区别很重要,但只是在某些情况下。
对于想要在操作数据、打乱播放列表或触发视频游戏事件时挑选一个随机样本的用户来说,使用的究竟是伪随机数还是真随机数其实无关紧要。在这些案例中,随机度究竟有多真实其实并不影响结果的质量。
在某些案例中,使用伪随机数可能是有利的,比如说为科学研究挑选一个随机样本时。在这种情况下,使用伪随机数能让其他人通过使用同样的种子值来复现你的研究。在视频游戏领域,在测试游戏时能够触发同样的「随机」事件是非常有用的。
在另一些案例中,使用真随机数则要重要得多。在加密等应用中,使用真随机数是格外重要的,因为这有助于对数据的持续保护。类似地,在在线赌博应用中,博彩公司也需要有信心地保证二十一点(洗牌方式)、轮盘赌(球落点位置)和扑克机(转盘停止位置)得到结果的方式是真正随机的,否则他们就面临着算法被逆向工程并被人借此谋利的风险。
真随机性并没有大多数人想的那么重要
在涉及真随机性时,一个怪异之处是其行为往往不同于人们的预期。以下面两张图为例——你觉得其中哪个是随机分布,哪个又是刻意创建/调整的?

如果你说是右图,你并不孤单,因为大多数人都预期随机性看起来应该是这个样子。但是,这是一个为了确保点分散平均而经过调整的相对均匀的分布。事实上,有空白和点群的左图才反映了一个真实随机分布。正是随机性这种产生群块和空白的趋势导致某些结果不符合我们的直觉。
以数字音乐服务 Spotify 为例。多年以来,Spotify 用户一直在抱怨播放列表随机混洗的质量。事实上,Spotify 的打乱列表功能的质量一直都备受讨论,如果你用谷歌搜索「Spotify shuffle」,自动完成结果里面「sucks」会出现在前排位置。Spotify 调查了这个问题,发现最常见的主题是来自同一位艺术家的音乐会一首接一首地频繁播放。简而言之,人们期望的随机性与现实不符。Spotify 在这篇有趣的文章中给出了解释:他们的打乱列表功能实际上是随机的,但他们现在已经进行了调整,以使其更符合人们心目中随机性。他们的方法是降低随机性,使得来自同一艺术家的歌曲会在播放列表中被分开。
赌徒谬误
正如 Spotify 的文章指出的那样,这个例子很好地表现了人们对随机性的期望与随机性的真实本质之间的不一致,这种现象被称为「赌徒谬误(gambler’s fallacy)」。赌徒谬误可以总结为两点:
- 相信独立随机事件(比如掷硬币、掷骰子)具有某种固有的趋向于平均值的性质。举个例子,当掷硬币时,如果出现了连续正面朝上的情况,就相信背面朝上的可能性会增大,因为最终分布会趋近于正面背面五五开。
- 由于上述信念,人们往往低估结果继续连续(或聚集)的可能性。这种情况的一个经典示例是轮盘赌桌上的人在看过之前结果的列表后,如果看到连续出现了五个黑色数字,就会相信下一个数字为红色的可能性会更高。顺便一提,赌场就是这样展示历史记录的,从而引诱人们押注他们认为更有利的结果。
如要检验你自己对连续出现同样结果的可能性的信念,可以假想你在赌场中的一个轮盘赌桌前。假设这家赌场每天营业 12 小时,而它平均每分钟转一次,那么每天就能转 720 次。假设出现红色数字和黑色数字的概率都是 50%(为了简单,我们忽略绿色的 0 和 00 情况),你认为一天里连续出现 8 次或更多次黑色或红色数字的概率是多少?
答案是大于 75%。换句话说,平均四天中有三天都会出现至少一组 8 次或更多次的黑色或红色数字连击。不仅如此,每天有 30% 的几率出现至少 10 次的连击,出现 12 连击的概率大约为 8%。你可以使用这个方便的计算器检验这些结果:Streak Calculator。
这意味着什么?
在你的日常生活,切勿贪多。如果你是赌徒,你也许应该收手了,但我敢肯定我不是第一个告诫你的人。如果你听信那些选股人的话,希望你重新考虑考虑他们的所谓「技术」中究竟有多少是纯粹的巧合,尤其还要考虑到幸存者偏差 1。也许这篇文章能帮你劝说你的朋友。
如果你没有这些问题,希望这篇文章能让你了解些有趣的知识和重要的应用。
[1] 在这个语境中存在幸存者偏差,因为那些没有选对股票的人不会再继续写文章。随着时间推移,只留下了那些选对了股票的人(即「幸存者」)还在继续写,即使他们选对的概率是完全随机的。
