【哲学史纲】米利都学派——毕达哥拉斯学派

米利都学派：

古希腊第一支哲学学派，以泰勒斯，阿那克西曼德，阿那克西美尼为代表，主要关注自然哲学中的本体论问题。总体看来米利都学派并没有突破此岸世界的束缚。

泰勒斯：

泰勒斯是古希腊第一位哲学家，他认为，“万物生于水，万物复归于水。”“水”是组成万物最基础“一”。因此，“水”作为本源不同于其他感性物，“水”同其他感性物之间是“一”与“多”的关系。此概念被其助手阿纳克西曼德继承，并发展为“无限”的概念。

泰勒斯之所以选择“水”作为本原，由以下两点主要原因，一是正如亚里士多德在《形而上学》中所记载的那样，“促进万物生长的东西都是潮湿的...而水则是潮湿事物的本性的起源。”二是本源的性质是无规定的，也就是我们要在后面提到的无限（不定/无定形）。本原一旦被认定为是有规定的，那么本原就不再是开端，也就不是本原了。因此“水”的形式是不受限定的，它更符合本原所要求的无规定性的性质。

阿那克西曼德：

阿纳克西曼德是泰勒斯的助手，阿纳克西曼德第一次提出了“始基”与“无限”的的概念。一切万物以始基为开端并复归于它。无限的内涵是无限定，无规定性，在后续埃利亚学派的解释中被理解为无界定的，无边界的含义。

首先“无限”概念的相对于“水”而言是更具由普遍性的。“无限”并不是直接来源于自然的感性物之中（这一点是对“水”与其他感性物之间的区分的进一步发展）。其次，无限是不断运动的，无限在运动中发展出有定型的感性物，从而无限并不是一个静态僵死的物，而是一个不断运动的活物。

阿那克西美尼：

阿那克西美尼是阿那克西曼德的助手，阿那克西美尼认为“气”是万物的本原。首先“气”具有唯一性，气不同于“无限”是一个过程，气区别于其他“伪无限”的感性物（比如说水）。其次“气”具有中介性，“气”稀释时变成“火（最不定的）”，凝聚时一次变成“风”“云”“水”“土”“石”，气作为中介的运动具有永恒性。

无限问题：

无限问题的提出源自于米利都学派无法调和无限（无定形）作为始基与有限（有定形）之间的关系。换句话来说就是无法解决无定形的“一”如何派生出有定形的“多”的问题。这个问题在毕达哥拉斯，赫拉克利特与巴门尼德三位哲学家所处的阶段中被讨论。

毕达哥拉斯学派：

毕达哥拉斯不同于毕达哥拉斯学派，毕达哥拉斯是毕达哥拉斯学派的创始人。毕达哥拉斯学派是一个及其分散的宗教政治组织，其学派内部是相互独立的。毕达哥拉斯学派的观点于公元前5世纪被菲洛劳斯（Philolaus）集中整理而成。

“无限”与“有限”，“形式”与“质料”：

毕达哥拉斯最大的贡献在于提出了形式，从而确立了“质料”与“形式”的关系。前苏格拉底哲学中，“形式”并不对应着“一”，“质料”并不对应着“多”。它以一种相反的形式呈现出来。阿那克西曼德所提出的“无限”是实体，其所对应的恰恰是成为“一”的“质料”，而毕达哥拉斯学派所提出的“数”（有限）是超越感性物的实在，其所对应的恰恰是成为“多”的“形式”。

数：

毕达哥拉斯学派对“数”的理解是基于对几何的理解之上的，“数”是毕达哥拉斯学派在对几何进行研究中发现的，换句话来说就是毕达哥拉斯学派发现了形式（数）与质料（感性物）之间的关系（量度，秩序，比例），因此数的性质同时也具有几何的性质。

例：琴弦的长短（几何性质的数）决定了琴弦振动所发出的音调。

因此，毕达哥拉斯学派也就确立了“一”组成“数”（多），“数”（多）组成点，点组成线，线组成面，面组成体，体组成元素的这种由数学向物理过度的创世说。从而毕达哥拉斯学派取消了无定形（无限）的本原地位，而用有定形（有限）的“数”来解释无定形（无限）的感性物。因此“数”也就是万物的尺度。但是“数”也存在着问题，“数”静止的性质决定了数无法被用来解释运动。这个问题，将会通过赫拉克利特对“数”的改造来解决。赫拉克利特将会继承毕达哥拉斯学派对“数”与感性物之间的关系的理解，来提出罗格斯（Logos）的概念。

“奇数”与“偶数”：

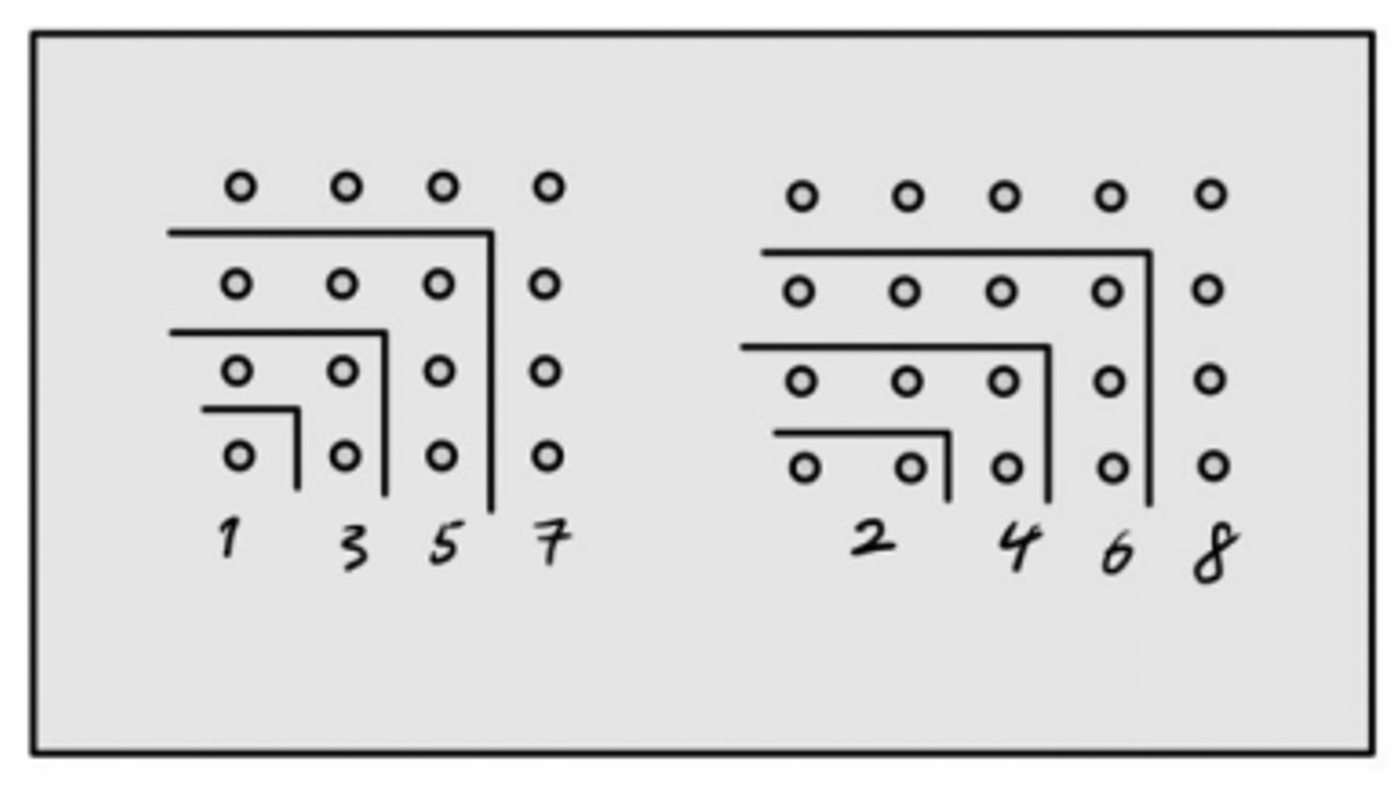
“奇数”是有限（有定形）的，而“偶数”是无限（无定形）的。 “一”既是“奇数”又是“偶数”，因此一既是“有限”的，又是“无限”的。奇数的无限相加会构成平方数，而偶数的无限相加会构成矩形数（如图1）。因为平方数的“长”“宽”比为1：1，所以平方数象征着稳定，也就是有限（有定形）。而举行数的“长”“宽”比是不确定的，所以矩形数也就象征着不定，也就是无限（无定形）。