刷起来 99 ~ 恢复 BST
基本信息
- 题号:99
- 题厂:未知(如有题友知道题厂信息来源,请麻烦告知,感谢)
- 难度系数:中
有一个 Binary Search Tree(BST),有两个节点的 value 值被置换了。请把这两个节点找出来再换回来,让树回归成一个合格的 Binary Search Tree(BST)
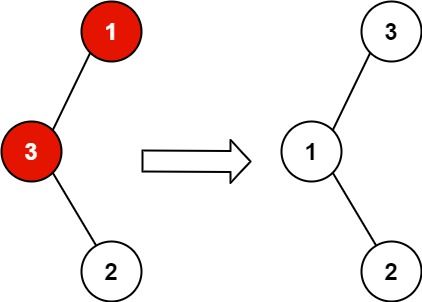
如图所示,1-3-2 的 BST 中,1-3 两个节点放反了,对换以后变成 3-1-2 满足 BST 的编排需求 。
root = [1,3,null,null,2] [3,1,null,null,2]
解题思路
这道题看似很玄幻,其实深入理解 BST 节点编排原理后,算法逻辑还是挺简单的🙈。
BST(Binary Search Tree):BST 是一种特殊的二分树,在 BST 中,一个节点左边的所有节点都比该节点小;一个节点右边的所有节点都要比该节点大……
- 了解了 BST 左右节点位置编排原理后,我们发现,如果将一个 BST 按 inorder 遍历,遍历出来的各节点 value 值输出顺序必然是按升序排列的。
- 换句话说,在节点数量一致,各节点 value 值一致的情况下,要满足节点成型 BST,无论谁做 root 节点,按照 inorder 遍历结果一定是各节点 value 值由小到大排列……
例如:有 3 个节点,value 值分别是 1, 2, 3.
- 如果选择 1 做根节点,那 2 和 3 只能当 1 的右节点
- 如果选择 2 做根节点,那 1 只能在 2 的左边,3 必然在 2 的右边才能满足 BST 的编排要求
无论 1 和 2 谁做根节点构造出来的 BST,按照 inorder 顺序遍历,输出一定是 1-2-3……
- 题目已知就两个节点放反了,所以我们把题目已知的 BST 按 inorder 遍历后,找出那两个没有按升序排列的节点,对换一下就可以了。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def recoverTree(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
# 初始化一个 temp 存放放节点
temp = []
# 写一个 dfs 方法按 inorder 遍历 BST,将各节点存放入 temp 中
def dfs(node):
if not node: return
dfs(node.left)
temp.append(node)
dfs(node.right)
dfs(root)
# 创建一个 sort 数组,将各节点 value 值按升序排列
srt = sorted(n.val for n in temp)
# for 循环一一比照节点值和对应 srt 值,进行置换
# 置换完成后,BST 也就恢复了……
for i in range(len(srt)):
temp[i].val = srt[i]
Constraints
The number of nodes in the tree is in the range [2, 1000].-231 <= Node.val <= 231 - 1
测试
- 当就只有 2 个节点时
- 节点数量,各节点 value 值一致时,随意置换节点,选取不同节点做 root
- ……
Big O
时间复杂度:O(n)- 空间复杂度: O(n)
总结
- 本题复习了 BST 的节点 value 值与 inorder 的关联特征
- 还复习了用 dfs 做 inorder 遍历
- 中档题和简单题的区别在于:简单题考查你知不知道 inorder、BST……;中档题在掌握知识的基础上还需要活学活用……🙈
