进阶期权交易：包含Python 程式码的综合指南

8 月 18 日

选择权交易是一种先进且多功能的交易策略，为交易者提供了在各种市场条件下成长的大量机会。了解高阶期权交易的复杂性，包括期权希腊、波动性策略、定价模型和风险管理，对于成功至关重要。在本综合指南中，我们将深入研究高级期权交易的世界，涵盖从高级期权交易概述到策略及其实施的复杂性的所有内容。作为了解期权交易基础知识的交易者，本指南将为您提供有效驾驭复杂的高级期权交易世界所需的技能和见解。

进阶期权交易概述

期权（Options）又称为选择权（下文的期权与选择权都代指Options） ，它是一种金融衍生工具。当标的资产价格在设定时间段内超过约定的价格时，期权持有方拥有要求卖方按照约定价格买卖资产的权利，但非义务。

高级期权交易业务超越了看涨期权和看跌期权的基本买卖。它涉及期权合约的有用组合以实现特定的交易目标。

现在让我们来看看高级期权交易所需的概念。

进行高级期权交易时的要点高级期权交易有一些要点，它们是：

价差：涉及买卖同一标的资产具有不同执行价格或到期日的选择权合约。透过组合这些合同，您可以建立明确的风险和回报概况。
希腊字母：选择权希腊字母是代表影响选择权价格的关键因素的字母，包括Delta、Gamma、Vega、Theta 和Rho。了解希腊人对于分析和管理选择权部位至关重要。
波动性：高阶策略通常利用波动性预期。有些策略从高波动性中受益，而有些策略则在低波动性环境中获利。（您可以在本课程中了解有关高级波动率交易的所有内容。）

高级期权交易涉及的策略一些常见的高级期权交易策略是：

多头跨式选择权和宽跨式选择权（Long Straddle and Strangle）：买入到期日相同、行使价不同的买权和卖权。
铁秃鹰和铁蝴蝶（Iron Condor and Iron Butterfly:）：结合熊市买权价差和牛市卖权价差。
日历价差（Calendar Spread）：卖出一份近期选择权并买入一份具有相同执行价格的长期选择权。
蝴蝶价差（Butterfly Spread:）：一种有限风险、有限报酬的选择策略。

此外，了解何时尽早行使（买入/卖出）选择权以获取潜在收益或避免不必要的任务对于高阶策略至关重要。

接下来，让我们看看为什么期权交易对交易者如此有吸引力。

为什么期权交易有吸引力？

选择权交易吸引交易者的原因有几个，以下是上诉的详细内容：

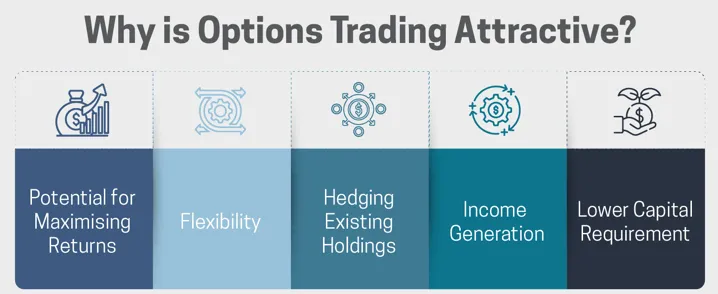
回报最大化的潜力：选择权提供了放大回报的潜力，特别是对于较小的初始投资。这种杠杆可能很有吸引力，但它也放大了潜在的损失，可以透过适当的风险管理技术来管理。
灵活性：选择权提供了比单纯买卖股票更广泛的策略。交易者可以在各种市场条件（看涨、看跌、中性或波动）下建立头寸以增加交易量。与基本股票交易相比，这种灵活性可能带来更高的回报。
对冲现有持有量：选择权可用于对冲现有股票头寸，作为针对价格波动的一种保险形式。透过策略性地购买看跌期权，交易者可以限制其所持股票的潜在损失。
创收：即使标的股票价格保持不变，某些选择权策略（例如出售备兑买权）也可以产生回报。这对于注重收入的投资者来说很有吸引力。
较低的资本要求：与直接购买股票相比，选择权通常需要较小的初始投资，从而允许交易者以较少的资本控制相同的标的资产。这对于资金有限的交易者来说可能很有吸引力。

然而，必须承认期权交易也存在一些风险。这些风险包括整个投资的潜在损失、由于时间衰减而导致的价值快速损失以及选择策略的复杂性，这可能会导致意想不到的结果。因此，交易者彻底了解选择权交易并采用风险管理策略来保护自己的投资至关重要。

主要期权希腊字母

主要选择权希腊字母是一组五个字母，代表影响选择权价格的关键因素。这些是选择权交易者分析和管理其头寸风险的基本工具。

以下是每个希腊文的意思：

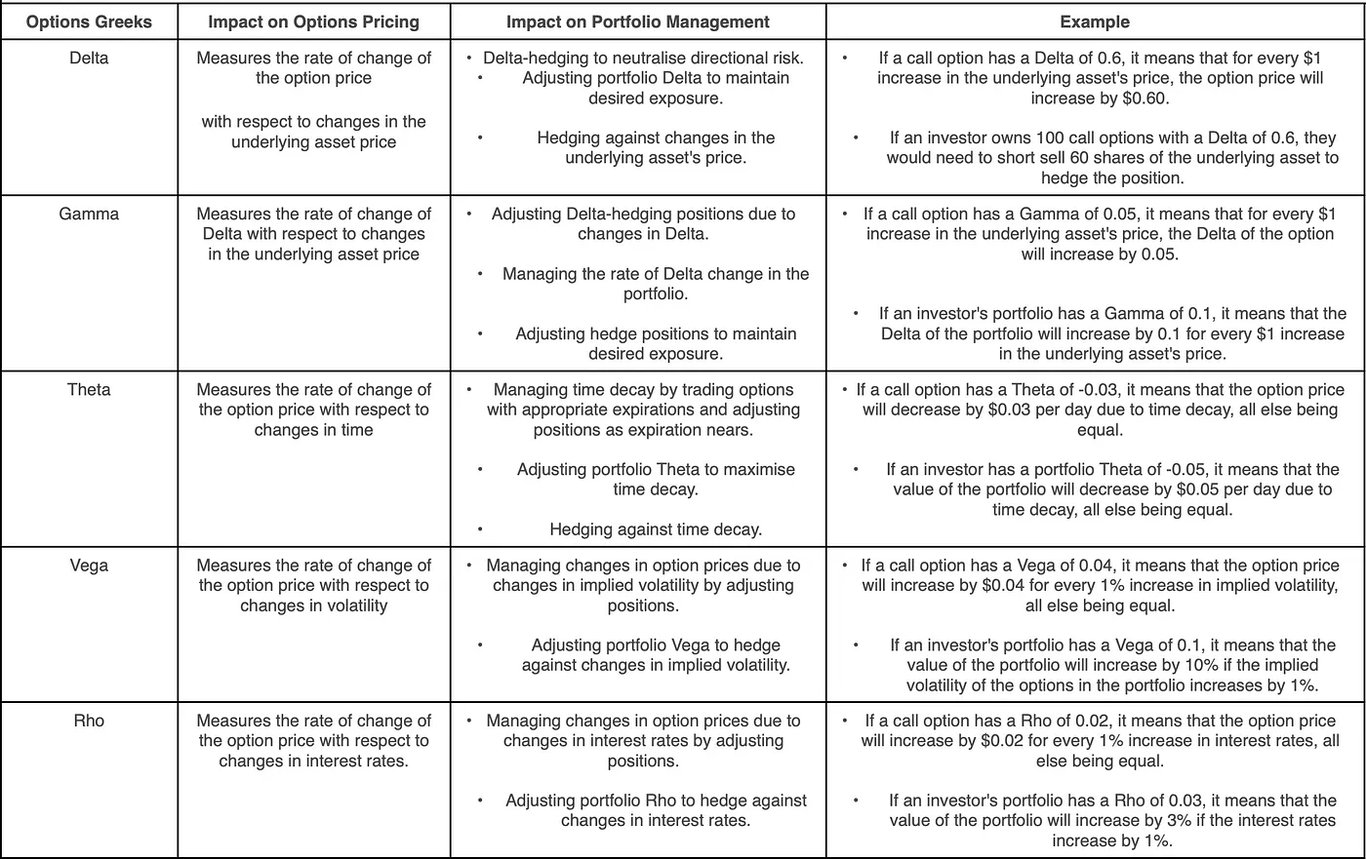
Delta德尔塔(Δ)

衡量选择权价格相对于标的资产（股票、债券等）价格1 美元变化的变化率。
买权的Delta 通常在0 到1 之间，表示其变动方向与标的资产相同，但幅度较小。
看跌期权的Delta 通常介于-1 和0 之间，表明它将朝着与标的资产相反的方向移动。

Gamma伽玛(γ)

代表Delta的变化率。它告诉您随着标的资产价格的变动，Delta 本身会发生多少变化。
正的Gamma 表明Delta 正在增加，这意味着选择权的价格将对标的资产价格的变化变得更加敏感。
负Gamma 表示Delta 正在减少，这意味着选择权的价格对标的资产价格变化的敏感度将降低。

Theta西塔(θ)

衡量由于时间的推移而导致的期权价格衰减率，也称为时间衰减。
在其他条件相同的情况下，选择权越接近到期，其价格就越低（Theta 为负值）。
Theta 对于短期选择权策略尤其重要，因为时间衰减会迅速侵蚀利润。

Vega织女星(ν)

衡量选择权价格对隐含波动率变化的敏感度。
隐含波动率反映了市场对标的资产未来价格波动的预期。
高Vega 表示选择权的价格对隐含波动率的变化较为敏感。相反，Vega 较低则表示价格受到的影响较小。

Rho罗(ρ)

衡量选择权价格对利率变化的敏感度。
一般来说，较高的利率会导致选择权价格略低，反之亦然。然而，与其他希腊人相比，Rho 的影响通常较小。

接下来，我们将详细讨论选择权希腊人对选择权定价的影响。

期权希腊字母对选择权定价与投资组合管理的影响

在这里，我们将再次看到主要的期权希腊人，但将讨论每个希腊人对期权定价和投资组合管理的影响，并提供每个例子。选择权希腊人对选择权价格对各种市场因素变化的反应以及投资组合管理都有特定的影响。

现在我们将了解实施高阶选择权交易策略所需的技能。

实施高阶期权交易策略的技能

以下是您需要培养的一些基本技能，以便透过高级期权交易策略取得成功：

技术知识

深入了解选择权希腊人：掌握Delta、Gamma、Theta、Vega 和Rho 至关重要。您应该能够解释它们对选择权定价和投资组合行为的影响。
波动率分析：能够评估历史波动率和隐含波动率以及影响波动率的因素，对于制定基于波动率的策略至关重要。
高阶选择权定价模型：虽然基本的Black-Scholes 模型可能足以满足某些策略的需要，但了解Heston 或SABR 等更复杂的模型可以更深入地了解选择权定价动态，尤其是在波动的市场中。
风险管理技术：进阶策略通常涉及管理多条腿（买入/卖出不同的选择权）。 Delta 对冲和利差调整等技术对于降低风险至关重要。
投资组合建构：能够结合不同的选择权策略来实现特定的风险回报状况并对现有资产进行对冲是一项宝贵的技能。

分析能力

市场分析：高阶策略通常依赖特定的市场前景或波动性预期。需要强大的分析能力来解释市场数据和技术指标，以做出明智的决策。
回测策略：使用历史资料测试策略的能力（回测）有助于评估其潜在表现并在拿实际资本冒险之前识别弱点。
情境分析：考虑您的部位对不同市场情境（上涨/下跌、波动性变化）的反应对于风险管理至关重要。

交易技巧

纪律与耐心：高阶策略通常需要等待特定市场条件的出现。纪律和耐心对于避免偏离计画的冲动交易至关重要。
订单管理：了解不同的订单类型（市价订单、限价订单、止损订单）以及如何有效使用它们对于管理部位的进场和出场至关重要。
情绪控制：选择权交易的快节奏和潜在的波动性可能会引发情绪反应。保持情绪控制并坚持您的交易计划对于成功至关重要。

额外技能

编码技能：在当今技术驱动的交易领域，基本编码知识(Python) 有助于回测策略、自动化计算或使用高级期权定价模型。
研究技能：随时了解选择权交易策略、市场趋势和相关财经新闻的新发展对于持续学习和适应非常重要。

现在让我们看看看跌期权平价意味着什么以及更多相关内容。

Python 中的看涨期权平价是什么？

卖权平价（PCP）是欧式买权、欧式卖权、标的资产价格、无风险利率与到期时间的关系。它本质上规定，根据执行价格的现值调整的看涨期权的价格应等于看跌期权的价格加上当前股票价格。

以下是一个Python 程式码，用于计算看跌期权奇偶校验并评估其对于给定参数集的有效性：

S：目前股价
K：执行价格
C：买权价格
P：卖权价格
r：无风险利率（年化）
T：到期时间（以年为单位）

它使用以下公式计算看跌期权平价：

C — e^(-rT) * K = P + S

然后，函数显示方程式的左侧(LHS) 和右侧(RHS)，以及它们之间的差异。它还检查差异是否接近零，表明看跌期权平价大致成立。

这是Python 程式码：

 import math def calculate_put_call_parity(S, K, C, P, r, T): # Left-hand side (LHS) of Put-Call Parity lhs = C - math.exp(-r * T) * K # Right-hand side (RHS) of Put-Call Parity rhs = P + S # Difference between LHS and RHS parity_difference = lhs - rhs print("Put-Call Parity Calculation:") print(f"Left-hand side (LHS): Call option price adjusted for present value of strike - {lhs}") print(f"Right-hand side (RHS): Put option price + Stock price - {rhs}") print(f"Difference between LHS and RHS: {parity_difference}") # Check if Put-Call Parity approximately holds (small difference due to rounding) if abs(parity_difference) < 1e-5: print("Put-Call Parity approximately holds.") else: print("Put-Call Parity does not hold.") return parity_difference # Example usage: S = 100 # Stock price K = 110 # Strike price C = 5 # Call option price P = 7 # Put option price r = 0.05 # Risk-free interest rate (5%) T = 1 # Time to expiration (in years) parity_difference = calculate_put_call_parity(S, K, C, P, r, T)

Output:

 Put-Call Parity Calculation: Left-hand side (LHS): Call option price adjusted for present value of strike - -99.63523669507855 Right-hand side (RHS): Put option price + Stock price - 107 Difference between LHS and RHS: -206.63523669507856 Put-Call Parity does not hold.

接近零的值表示奇偶校验成立，但在上面的输出中，它表明看跌期权奇偶校验不成立。

接下来让我们转向期权定价。

期权定价

选择权定价涉及确定选择权合约的公允价值，这赋予持有人以以下价格购买（如果是看涨选择权）或出售（如果是看跌选择权）标的资产的权利，但没有义务。价格）。

下面您将看到两种类型的选择权定价技术以及它们之间的差异。这些类型是：

选择权的内在价值
选择权的时间价值

选择权的内在价值

选择权的内在价值是指选择权立即行使时所具有的价值。

下面您可以看到它们是如何计算的。

 Intrinsic Value of Call Option = Current Market Price of Underlying Asset - Strike Price Intrinsic Value of Put Option = Strike Price - Current Market Price of Underlying Asset

选择权的时间价值

选择权的时间价值是指选择权买方为在到期前拥有选择权的特权而支付的权利金。它反映了期权在到期时最终成为价内期权的机率。

 Time Value = Option Premium - Intrinsic Value

展望未来，我们将了解选择权定价模型。

期权定价模型

选择权定价模型是用来决定选择权公允价值的数学模型。您将在下面找到不同的期权定价模型以及每个模型之间的主要差异。

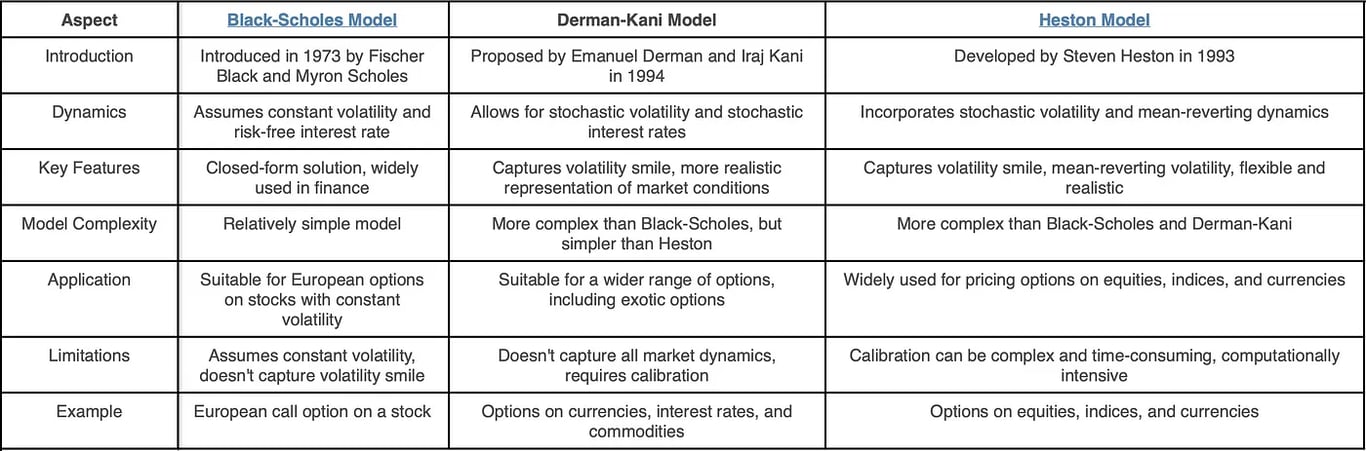
每种模型都有其优点和局限性，模型的选择取决于交易者或投资者的特定要求。

现在让我们来看看最受欢迎的高阶选择策略之一，即蝴蝶策略及其收益图。

使用Python 的蝴蝶期权交易策略范例

要获得蝴蝶策略的收益图，您需要遵循以下步骤：

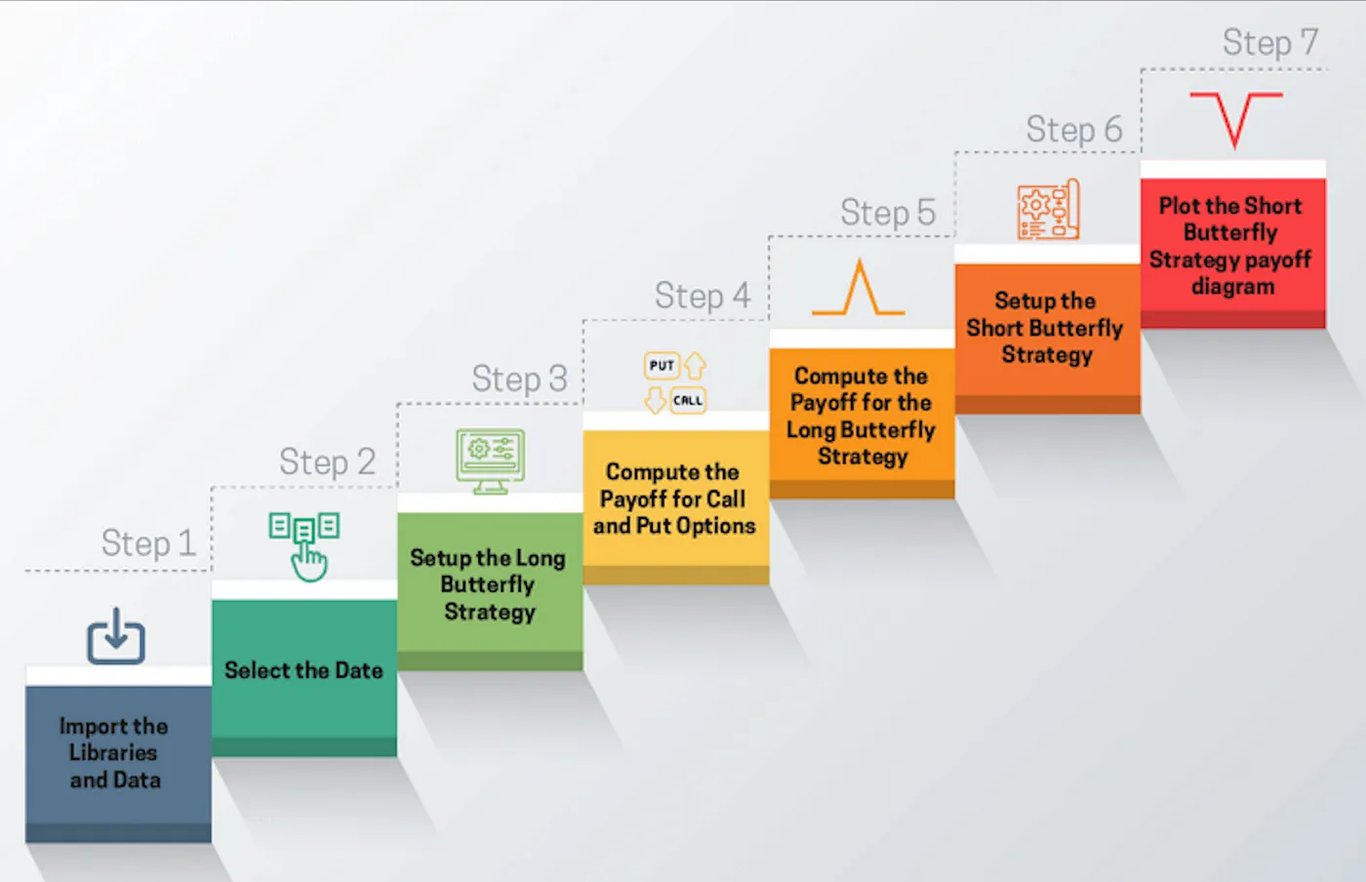
建立策略并了解您将使用什么类型的选项。
了解每个选择权将使用哪个执行价格。
选择一个价格范围，您将与该价格范围比较每个选择权的收益。
将策略效益计算为蝴蝶策略中使用的所有选项的收益总和。
根据价格范围绘制策略收益。

学习此策略后，您将能够绘制您可能想要设定的任何选择权策略的收益图。

步骤如下：

 # For data manipulation import pandas as pd import numpy as np # For data visualisation import matplotlib.pyplot as plt %matplotlib inline plt.style.use('seaborn-darkgrid') # For option's payoff computations import sys sys.path.append('..') from data_modules.options_util_quantra import setup_butterfly # Read the options data options_data = pd.read_pickle('../data_modules/nifty_options_data_2019_2022.bz2') # Read the futures data futures_spot_data = pd.read_pickle( '../data_modules/nifty_data_2019_2022.bz2')[['futures_close', 'Expiry']] # Print the last 5 rows of the futures data futures_spot_data.tail()

输出：

 futures_close ExpiryDate 2022-05-20 16253.25 2022-05-262022-05-23 16183.35 2022-05-262022-05-24 16104.70 2022-05-262022-05-25 16013.80 2022-05-262022-05-26 16159.05 2022-05-26

第2 步：选择日期

# Set the analysis dateanalysis_date = "2021-01-01"# Fetch the futures close price that corresponds to the above datefutures_price = futures_spot_data.loc[analysis_date, 'futures_close']# Fetch the options chain data that belongs to the above dateoptions_chain = options_data.loc[analysis_date]# Print the futures close price of the datef"The futures price on {analysis_date} is {futures_price}"

Output:

 'The futures price on 2021-01-01 is 14053.85'

 # Print the options chain data of the above date options_chain.head()

 Symbol Expiry Option Type Strike Price Open High Low Close Last Settle Price Number of Contracts Turnover Premium Turnover Open Interest Change in OI Underlying Date 2021-01-01 NIFTY 28-01-2021 CE 12000 2017.10 2062.25 2014.0 2043.60 2042.00 2043.60 256.0 269606000.0 39206000.0 456225.0 10200.0 14018.5 2021-01-01 NIFTY 28-01-2021 CE 12050 0.00 0.00 0.0 609.75 0.00 2009.45 0.0 0.0 0.0 0.0 0.0 14018.5 2021-01-01 NIFTY 28-01-2021 CE 12100 1923.15 1936.45 1922.6 1934.75 1934.75 1960.25 4.0 4209000.0 579000.0 15750.0 0.0 14018.5 2021-01-01 NIFTY 28-01-2021 CE 12150 0.00 0.00 0.0 569.95 0.00 1911.10 0.0 0.0 0.0 0.0 0.0 14018.5 2021-01-01 NIFTY 28-01-2021 CE 12200 0.00 0.00 0.0 1797.80 1799.00 1862.15 0.0 0.0 0.0 22575.0 0.0 14018.5

步骤三：制定多头蝴蝶策略

# Setup the butterfly strategybutterfly = setup_butterfly(futures_price, options_chain, "long")# Print the strategy dataframebutterfly

Output:

 Option Type Strike Price position premium0 CE 14050 -1 280.751 PE 14050 -1 279.002 CE 14600 1 69.253 PE 13500 1 103.00

步骤四：计算买权和卖权的收益

既然我们已经建立了多头蝴蝶策略，现在让我们计算买权和卖权的收益。请记住，多头买权的收益由下式给出：

Long Call Payoff=𝑀𝑎𝑥(Spot Price−Strike Price,0)−Premium

Max 函数解释如下：

如果现货价格高于执行价格，则多头买权收益为现货价格与执行价格之间的差额。
如果现货价格低于执行价格，则多头买权收益为0。

你能猜出如何计算空头买权吗？很简单，您只需将上述函数乘以-1 即可获得卖空版本的看涨期权收益。

定义呼叫支付函数

# Setup the butterfly strategy butterfly = setup_butterfly(futures_price, options_chain, "long") # Print the strategy dataframe butterfly

Output:

 Option Type Strike Price position premium 0 CE 14050 -1 280.75 1 PE 14050 -1 279.00 2 CE 14600 1 69.25 3 PE 13500 1 103.00

第5 步：计算多头蝴蝶策略的效益

# Compute long call payoff value call_payoff_value = call_payoff(16000, 15000, 20, 1) # Print the long call payoff value call_payoff_value

Output:

 # Compute the short call payoff value call_payoff_value = call_payoff(16000, 15000, 20, -1) # Print the short call payoff value call_payoff_value

Output:

 - 980

然后，类似地，我们可以定义看跌期权收益。

对于多头看跌期权收益，我们有以下公式及其解释：

多头卖权收益= 𝑀𝑎𝑥(行使价−现货价格,0)−权利金

如果执行价格高于现货价格，则多头卖权收益为执行价格与现货价格之间的差额。
如果执行价格低于现货价格，则多头卖权收益为0。

 # Define the put payoff function def put_payoff(spot_price, strike_price, premium_spent, position): return (np.maximum(strike_price - spot_price, 0) - premium_spent) * position # Compute the long put payoff value put_payoff_value = put_payoff(16000, 15000, 20, 1) # Print the long put payoff values put_payoff_value

Output:

-20

最后，空头卖权收益值：

 # 計算空頭看跌期權收益值put_payoff_value = put_payoff(16000, 15000, 20, -1) # 列印空頭看跌期權收益值put_payoff_value

输出：

第6 步：制定空头蝴蝶策略

def get_payoff(spot_price_expiry, options_strategy): # Create a payoff column with empty values options_strategy['payoff'] = np.nan # Create a loop to go through each option that belongs to the butterfly strategy for i in options_strategy.index: # Check if the option is a call if options_strategy.loc[i, 'Option Type'] == 'CE': # Compute the call payoff as per its corresponding values options_strategy.loc[i, 'payoff'] = call_payoff( spot_price_expiry, options_strategy.loc[i, 'Strike Price'], options_strategy.loc[i, 'premium'], options_strategy.loc[i, 'position']) # Check if the option is a put elif options_strategy.loc[i, 'Option Type'] == 'PE': # Compute the put payoff as per its corresponding values options_strategy.loc[i, 'payoff'] = put_payoff( spot_price_expiry, options_strategy.loc[i, 'Strike Price'], options_strategy.loc[i, 'premium'], options_strategy.loc[i, 'position']) # Return the payoff sum of the 4 options return options_strategy['payoff'].sum()

让我们举个例子。让我们针对特定价格呼叫get_payoff 函数，看看到期时的价值是多少。

 get_payoff(13100, butterfly)

Output:

 -162.5

 # Create the payoff dataframe payoff = pd.DataFrame() # Compute the price range payoff['price_range'] = options_chain['Strike Price'].unique() # Print the last 5 rows of the price range of the payoff dataframe payoff['price_range'].tail()

Output:

 66 15300 67 15350 68 15400 69 15450 70 15500 Name: price_range, dtype: int64

 # Compute the butterfly strategy payoff values payoff['pnl'] = payoff.apply( lambda r: get_payoff(r.price_range, butterfly), axis=1) # Print the last 5 rows of the strategy payoffs payoff['pnl'].tail()

Output:

 66 -162.5 67 -162.5 68 -162.5 69 -162.5 70 -162.5 Name: pnl, dtype: float64

 # Set price_range as index payoff.set_index('price_range', inplace=True) # Set figure size plt.figure(figsize=(15, 7)) # Plot the payoff data plt.plot(payoff) # Set the title and labels and their sizes plt.title('Long Butterfly Strategy Payoff Diagram', fontsize=16) plt.xlabel('Price (Rupees)', fontsize=15) plt.ylabel('Payoff (Rupees)', fontsize=15) plt.tick_params(axis='both', labelsize=15) # Show the graph plt.show()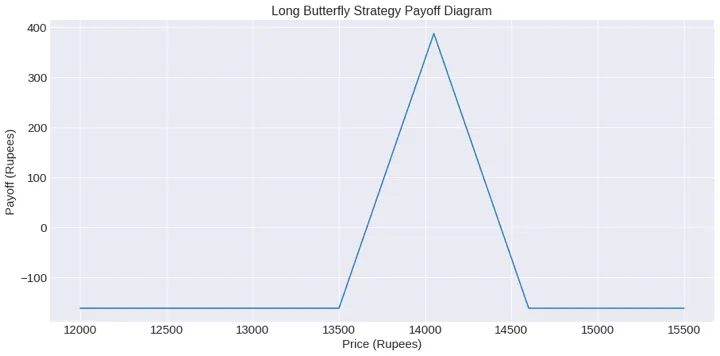

 # Print the maximum expected profit for the strategy max_profit = round(payoff.max(),2)[0] # Print the futures price corresponding to the maximum profit max_profit_futures_price = payoff.idxmax()[0] f"The maximum profit is {max_profit} and its corresponding futures price is {max_profit_futures_price}"

Output:

 'The maximum profit is 387.5 and its corresponding futures price is 14050'

因此，如果到期时的期货价格为14050，则该策略的最大利润预计为387.5 卢比。

 # Print the maximum expected loss for the strategy max_loss = round(payoff.min(),2)[0] # Print the futures price corresponding to the maximum loss max_loss_futures_price = payoff.idxmin()[0] f"The maximum loss is {max_loss}"

Output:

 'The maximum loss is -162.5'

第7 步：绘制空头蝴蝶策略收益图

# Setup the butterfly strategy dataframe butterfly = setup_butterfly(futures_price, options_chain, "short") # Print the short butterfly dataframe butterfly

输出：

 Option Type Strike Price position premium 0 CE 14050 1 280.75 1 PE 14050 1 279.00 2 CE 14600 -1 69.25 3 PE 13500 -1 103.00

 # Create the payoff dataframe payoff = pd.DataFrame() # Create the price range based on the strike prices of the options chain payoff['price_range'] = list(options_chain['Strike Price'].unique()) # Compute the payoff values for the short butterfly strategy payoff['pnl'] = payoff.apply( lambda r: get_payoff(r.price_range, butterfly), axis=1) # Set price_range as index payoff.set_index('price_range', inplace=True) # Set figure size plt.figure(figsize=(15, 7)) # Plot the payoff data plt.plot(payoff) # Set the title and labels and their sizes plt.title('Short Butterfly Strategy Payoff Diagram', fontsize=16) plt.xlabel('Price (Rupees)', fontsize=15) plt.ylabel('Payoff (Rupees)', fontsize=15) plt.tick_params(axis='both', labelsize=15) # Show the graph plt.show()

Output:

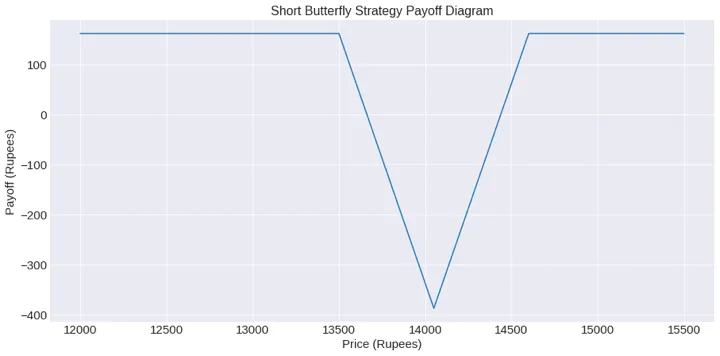
正如您所看到的，收益图让我们直观地了解何时可以透过多头或空头蝴蝶策略获得最大回报。上面的程式码可用于您想要获得的任何策略效益。

您可以透过系统选择权交易课程查看整个策略以及更多有关蝴蝶策略的资讯。本课程也将帮助您详细学习回测期权交易策略和相关概念。

值得注意的是，回测结果并不能保证未来的表现。所提供的策略结果仅用于教育目的，不应被解释为投资建议。有必要对多个参数的策略进行全面评估，以评估其有效性。

现在，我们将了解如何在高级选择权交易中进行风险管理。

进阶期权交易中的风险管理

风险管理对于高级期权交易至关重要，可以保护您的资本并优化您的回报。

以下是高阶选择权交易的一些关键风险管理策略：

头寸规模：确定您愿意在任何单笔交易中承担风险的最大资本金额。这可以确保您不会过度暴露于任何一种职位。
多元化：透过不同标的资产、产业和策略的选择权交易多元化来分散风险。
止损订单：使用停损订单来限制选择权部位的潜在损失。根据您的风险承受能力和标的资产的波动性设定停损水准。
对冲：使用买入保护性看跌期权或卖出有担保看涨期权等策略对冲您的期权头寸，以抵消潜在损失。
波动性管理：了解波动性对选择权价格的影响并相应调整您的部位。考虑使用从波动性变化中受益的策略，例如跨式选择权或宽跨式选择权。
风险报酬率：在选择权交易中保持有利的风险报酬率。目标是潜在回报远远超过潜在风险的交易。
定期监控：定期监控您的选择权头寸，并准备好在市场状况发生变化或您的交易理论不再成立时调整或平仓。
风险分析工具：在进行选择权交易之前，使用经纪商或第三方软体提供的风险分析工具来评估选择权交易的潜在风险和回报。
部位调整：制定计画来调整或平仓未如预期执行的选择权部位。这可能涉及将头寸展期、调整执行价格或平仓亏损头寸以限制损失。
持续学习：随时了解市场趋势、经济指标等可能影响选择权价格的因素。不断学习先进的选择权交易策略和风险管理技术。

透过实施这些风险管理策略，您可以最大限度地降低下行风险，同时最大限度地提高高级选择权交易的潜在回报。

最后但并非最不重要的一点是，我们将看到可用于学习选择权交易的资源。

有关高级期权交易的常见问题

以下是选择权交易者通常会问的问题。因此，我们已经为前面的每个问题提供了答案。

Q：进阶交易中影响选择权定价的主要因素有哪些？
答：高级交易中的选择权定价受以下几个因素影响：

标的资产价格：标的资产的当前价格显著影响选择权的价值。
执行价格：执行价格与标的资产当前价格之间的关系会影响选择权的内在价值。
到期时间：选择权到期之前的剩余时间会影响其时间价值。
波动性：隐含波动性衡量市场对未来波动性的预期，对选择权定价有重大影响。
利率：利率的变动会影响选择权现金流的现值。
股利：对于股票选择权，股利支付的时间和规模会影响选择权定价。

Q：如何选择合适的选择权合约进行进阶交易？
答：选择正确的选择权合约需要考虑以下几个因素：

标的资产：根据您熟悉并深入分析的标的资产选择选择权合约。
市场状况：考虑当前的市场状况，包括波动性、趋势和流动性。
交易目标：确定您的交易目标，无论您是在寻求创造收入、投机还是对冲。
风险承受能力：评估您的风险承受能力并选择符合您的风险管理策略的选择权合约。
选择权希腊人：分析选择权希腊人以了解选择权价格对各种因素变化的敏感度。
到期日：选择与您的交易时间表和对标的资产的预期相符的到期日。

Q：隐含波动率在高阶选择权交易中发挥什么作用？
答：隐含波动率是选择权定价和高阶选择权交易的关键因素：

选择权定价：隐含波动率反映了市场对未来波动率的预期，是选择权定价模型的关键输入。
策略选择：高隐含波动率可能导致选择权定价过高，使卖出选择权等策略更具吸引力，而低隐含波动率可能有利于买入选择权。
风险管理：隐含波动率可以帮助交易者评估其选择权部位的潜在风险并相应调整策略。
市场情绪：隐含波动率的变化可以显示市场情绪的变化，并提供对未来价格趋势的洞察。

Q：在进阶期权交易中需要避免哪些常见错误？
答：在进阶期权交易中要避免的常见错误包括：

过度杠杆：相对于帐户规模而言，持仓量过大进行交易。
忽略风险管理：未能使用停损单或风险管理技术来限制损失。
忽略隐含波动率：选择选择权策略时不考虑隐含波动率。
缺乏多元化：交易集中在单一标的资产或策略，增加了投资组合风险。
追逐回报：只专注于潜在利润而不考虑潜在风险。
未能规划：没有明确的交易计画或策略进行交易。
忽视市场状况：未能根据当前市场状况调整交易策略。

Q：我如何及时了解与高阶选择权交易相关的市场动态？
答：您可以透过以下方式了解市场动态：

市场研究：定期查看财经新闻、市场分析和经济报告，随时了解可能影响选择权价格的动态。
技术分析：监控技术指标和图表模式以识别潜在的交易机会。
选择权教育：不断自我教育高阶选择权交易策略与风险管理技术。
专业分析：专注于市场分析师、交易员和金融专家，他们提供与选择权交易相关的见解和分析。
线上社群：加入线上论坛、交易社群和社群媒体群组，讨论交易想法并随时了解市场趋势。
经纪商工具：利用经纪商提供的研究工具和资源，例如市场扫描器、选择权筛选器和研究报告。

Q：我可以在不同的市场条件下使用高阶选择权交易策略吗？
答：是的，高阶选择权交易策略可以在各种市场条件下使用：

看涨市场：买权多头、卖权空头、买权价差和备兑买权等策略可用于看涨市场，从价格上涨中获利。
看跌市场：看跌市场中可以使用多头看跌期权、空头看涨期权、看跌期权价差和看涨期权价差等策略，从价格下跌中获利。
横盘市场：铁秃鹰、蝴蝶和日历价差等策略可用于横盘市场，从区间价格波动中获利。
高波动性市场：跨式选择权、宽跨式选择权和比率价差等策略可用于高波动性市场，从大幅价格变动或隐含波动性变动中获利。
结论
高级期权交易为寻求有效管理风险的投资者提供了大量的策略和工具。了解选择权希腊字母，即Delta、Gamma、Vega 和Theta 至关重要，因为它们直接影响选择权定价和投资组合管理。
波动性策略对于高阶选择权交易的成功至关重要，掌握实施这些策略所需的技能是关键。
了解期权如何定价、影响定价的因素以及各种期权定价模型是基础。风险管理至关重要，学习如何有效分析选择希腊人并避免常见错误对于成功至关重要。随时了解市场发展并利用可用资源（例如高级期权交易课程和书籍）对于持续学习和改进至关重要。
透过遵循正确的方法并利用正确的经纪商，交易者可以充满信心和能力地驾驭高级选择权交易的世界。
要了解有关高级期权交易的更多信息，我们的期货和期权市场量化交易学习路线涵盖了7 门课程，以开始在期货和期权交易中使用量化技术。透过这些课程，您将学习波动率预测、期权回测、风险管理、期权定价模型、希腊语以及各种策略，如跨式策略、蝴蝶策略、铁秃鹰策略、价差策略、离散交易、情绪交易、盒子策略、多元化期货交易策略还有更多。